力扣（leetcode）题目总结——二分法篇

leetcode 经典题分类

• 链表
• 数组
• 字符串
• 哈希表
• 二分法
• 双指针
• 滑动窗口
• 递归/回溯
• 动态规划
• 二叉树
• 辅助栈

本系列专栏：点击进入 leetcode题目分类 关注走一波

---

前言：本系列文章初衷是为了按类别整理出力扣（leetcode）最经典题目，一共100多道题，每道题都给出了非常详细的解题思路、算法步骤、代码实现。很多同学刚开始刷题都是按照力扣顺序刷题，其实这样对新手不太适用，刷题效果也很不好。因为力扣题目顺序是随机的，并没有按照算法分类，导致同一类型的算法强化训练不够，最后刷完也是迷迷糊糊的。所以本系列文章就是来帮你完成算法分类，针对每种算法做强化训练，保证让你以后遇到题目直接秒杀！

---

寻找两个正序数组的中位数

【题目描述】

给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2，请你找出并返回这两个正序数组的中位数。要求算法的时间复杂度为O(log(m+n))。

【输入输出实例】

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000 （合并数组 = [1,2,3]，中位数 2）

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000 （合并数组 = [1,2,3,4]，中位数 (2 + 3) / 2 = 2.5）

【算法思路】

看到时间复杂度为log级别，很明显，我们只有用到二分的方法才能达到。题目是求中位数，其实就是求第 k 小数的一种特殊情况，而求第 k 小数有一种算法。

我们每一次遍历就相当于去掉不可能是中位数的一个值，也就是一个一个排除。由于数列是有序的，其实我们完全可以一半一半的排除。假设我们要找第 k 小数，我们可以每次循环排除掉k/2个数。

举例如下，假设我们要找第 7 小的数字：

我们比较两个数组的第k/2个数字，如果k是奇数，向下取整。也就是比较第3个数字，上边数组中的4和下边数组中的3，如果哪个小，就表明该数组的前k/2个数字都不是第 k 小数字，所以可以排除。也就是1，2，3这三个数字不可能是第7小的数字，我们可以把它排除掉。将1 3 4 9和 4 5 6 7 8 9 10两个数组作为新的数组继续进行比较。

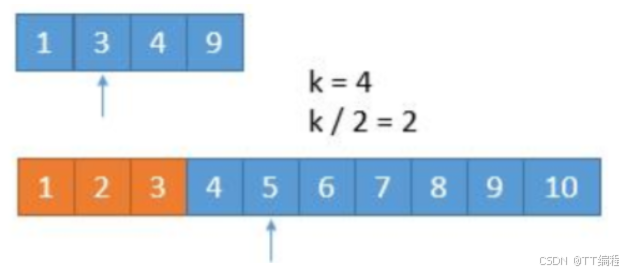
由于我们已经排除掉了 3 个数字，就是这 3 个数字一定在最前边，所以在两个新数组中，我们只需要找第7 - 3 = 4小的数字就可以了，也就是k = 4。此时两个数组，比较第2个数字，3 < 5，所以我们可以把小的那个数组中的1、3排除掉。

往后依次类推：

直到遇到k == 1时，表示已经最接近中位数了，选取nums1和nums2中较小的值就是第7小的数。

特殊情况：

每次都是取 k/2 的数进行比较，有时候可能会遇到数组长度小于 k/2的时候。

此时k/2等于3，而上边的数组长度是2，我们此时将箭头指向它的末尾就可以了。这样的话，由于2 < 3，所以就会导致上边的数组1、2都被排除。

由于上面数组2个元素都被排除，所以此时k = 5，我们只需要返回下边的数组的第 5 个数字就可以。

所以我们采用递归的思路，为了防止数组长度小于k/2，所以每次比较min(k/2, len(数组))对应的数字，把小的那个对应的数组的数字排除，将两个新数组进入递归，并且k要减去排除的数字的个数。递归出口就是当k == 1或者其中一个数组长度为0。

【算法描述】

/************** 暴力求解法(归并排序) **************/
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) 
{
    int len1 = nums1.size();
    int len2 = nums2.size();
    int len = len1 + len2;
    vector<int> v;  //合并后的有序数组
    int n1 = 0;  //遍历nums1容器的下标
    int n2 = 0;  //遍历nums2容器的下标
    //归并排序
    while(n1 < len1 && n2 < len2)
    {
        //按各数组的相对顺序从头开始依次比较，谁大放谁
        if(nums1[n1] <= nums2[n2])
        {
            v.push_back(nums1[n1++]);
        }
        else
        {
            v.push_back(nums2[n2++]);
        }
    }
    //某个数组先遍历结束，最后将另一个数组的剩余元素直接放入v
    while(n1 < len1)
    {
        v.push_back(nums1[n1++]);
    }
    while(n2 < len2)
    {
        v.push_back(nums2[n2++]);
    }
    if(len % 2 == 0)  //返回中位数
    {
        return (double)(v[len/2 - 1] + v[len/2]) / 2;
    }
    else
    {
        return (double)v[len/2];
    }
}

/************** 标准解法(递归找第k小的值) **************/
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
    int len1 = nums1.size();
    int len2 = nums2.size();
    int len = len1 + len2;
    if(len % 2 == 0)  //找中位数
    {
        return (double)(GetNum(nums1, 0, len1-1, nums2, 0, len2-1, len/2) 
        			+ GetNum(nums1, 0, len1-1, nums2, 0, len2-1, len/2 + 1)) / 2;
    }
    else
    {
        return (double)GetNum(nums1, 0, len1-1 ,nums2, 0, len2-1, len/2 + 1);
    }
}
//递归地从nums1[start1:end1]和nums2[start2:end2]联合中找第k小的值
int GetNum(vector<int>& nums1,int start1,int end1, vector<int>& nums2,int start2,int end2, int k)
{
    int n1 = end1 - start1 + 1;
    int n2 = end2 - start2 + 1;
    if(n1 > n2)  //保证nums1是位数小的容器
    {
        return GetNum(nums2, start2, end2, nums1, start1, end1, k);
    }
    if(n1 == 0)  //表示nums1中全部元素都低于中位数
    {
        return nums2[k + start2 -1];
    }
    if(k == 1)  //找第一个小的数，则比较nums1[start1]和nums2[start2]，返回较小值
    {
        return min(nums1[start1], nums2[start2]);
    }
    //一半一半地排除不是中位数的元素
    int i = start1 + min(n1, k/2) - 1;  
    int j = start2 + min(n2, k/2) - 1;
    if(nums1[i] > nums2[j])
    {
        return GetNum(nums1, start1, end1, nums2, j+1, end2, k-(j-start2+1));  //更新容器区间和k
    }
    else
    {
        return GetNum(nums1, i+1, end1, nums2, start2, end2, k-(i-start1+1));  //更新容器区间和k
    }
}

搜索旋转排序数组

【题目描述】

整数数组nums按升序排列，数组中的值互不相同。

在传递给函数之前，nums在预先未知的某个下标k上进行了旋转，使数组变为[nums[k], nums[k+1] ,…, nums[n-1], nums[0],nums[1] ,…, nums[k-1]]（下标从0开始计数）。例如，[0,1,2,4,5,6,7] 在下标3处经旋转后可能变为 [4,5,6,7,0,1,2]。

给你旋转后的数组nums和一个整数target，如果nums中存在这个目标值target，则返回它的下标，否则返回 -1 。

必须设计一个时间复杂度为O(log n)的算法解决此问题。

【输入输出实例】

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

【算法思路】

二分查找法：

将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也能是部分有序。判断是否有序，可以通过比较左边界点和分割点的大小来判断左边序列是否是有序的，即if(nums[left] <= nums[mid])。判断右边序列同理。

此时再判断target是否在有序部分的范围内：

• 如果在有序部分的范围，则用二分法在此区间查找；

• 如果不在有序部分，那么对无序部分再进行一分为二，其中一个一定有序，另一个可能有序，就这样循环。

【算法描述】

//二分查找
int search(vector<int>& nums, int target)
{
    int len = nums.size();
    int left = 0;  //左指针
    int right = len - 1;  //右指针
    while(left <= right)
    {
        int mid = (left + right) / 2;  //中点
        if(target == nums[mid])    //找到目标值
        {
            return mid;
        }
        if(nums[left] <= nums[mid])  //左边序列为有序序列
        {
            if(target >= nums[left] && target <= nums[mid])  //如果目标值在该区间内，则二分查找该区间
            {
                right = mid - 1;
            }
            else  //如果目标值不在该区间内，则去右区间查找
            {
                left = mid + 1;
            }
        }
        else  //右边序列为有序序列
        {
            if(target >= nums[mid] && target <= nums[right])  //如果目标值在该区间内，则二分查找该区间
            {
                left = mid + 1;
            }
            else  //如果目标值不在该区间内，则去左区间查找
            {
                right = mid - 1;
            }
        }
    }
    return -1;  //未找到
}

搜索旋转排序数组II

【题目描述】

已知存在一个按非降序排列的整数数组 nums ，数组可能包含重复元素。在传递给函数之前，nums 在预先的某个下标 k 上进行了旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]。例如， [0,1,2,4,4,4,5,6,6,7] 在下标 5 处经旋转后可能变为 [4,5,6,6,7,0,1,2,4,4] 。

给你旋转后的数组 nums 和一个整数 target ，请你编写一个函数来判断给定的目标值是否存在于数组中。如果 nums 中存在这个目标值 target ，则返回 true ，否则返回 false 。

你必须尽可能减少整个操作步骤。

【输入输出实例】

示例 1：

输入：nums = [2,5,6,0,0,1,2], target = 0
输出：true

示例 2：

输入：nums = [2,5,6,0,0,1,2], target = 3
输出：false

【算法思路】

本题基于 33、搜索旋转排序数组 的基础上作出修改，本题数组 nums 可能包含重复元素。

利用二分查找法：

将数组一分为二，其中一定有一个是有序的，另一个可能是有序，也可能是部分有序。判断是否有序，可以通过比较左边界点和分割点的大小来判断左边序列是否是有序的，即if(nums[left] <= nums[mid])。判断右边序列同理。但是对于数组中可能有重复元素的情况，二分查找时可能会有nums[left] == nums[mid] == nums[right]的情况，此时无法判断左区间和右区间哪个是有序的，只能将当前区间的左边界加一，右边界减一，直到能分出有序区间。

此时再判断target是否在有序部分的范围内：

• 如果在有序部分的范围，则用二分法在此区间查找；
• 如果不在有序部分，那么对无序部分再进行一分为二，其中一个一定有序，另一个可能有序，就这样循环。

【算法描述】

bool search(vector<int>& nums, int target) {
    int len = nums.size();
    int left = 0;   //左指针
    int right = len - 1;    //右指针
    while(left <= right)
    {
        int mid = (left + right) / 2;    //中点
        if(nums[mid] == target)
        {
            return true;
        }
        //遇到nums[left] == nums[mid] == nums[right]时，无法判断区间[left,mid]和[mid,right]哪个是有序的，只能将当前区间的左边界加一，右边界减一，直到能分出有序区间
        while(left < right && nums[mid] == nums[left] && nums[mid] == nums[right])
        {
            left++;
            right--;
        }
        if(nums[left] <= nums[mid])    //左边序列为有序序列
        {
            if(target >= nums[left] && target < nums[mid])  //如果目标值在该区间内，则二分查找该区间
            {
                right = mid - 1;
            }
            else  //如果目标值不在该区间内，则去右区间查找
            {
                left = mid + 1;
            }
        }
        else    //右边序列为有序序列
        {
            if(target > nums[mid] && target <= nums[right])  //如果目标值在该区间内，则二分查找该区间
            {
                left = mid + 1;
            }
            else  //如果目标值不在该区间内，则去左区间查找
            {
                right = mid - 1;
            }
        }
    }
    return false;
}

在排序数组中查找元素的第一个和最后一个位置

【题目描述】

给你一个按照****非递减****顺序排列的整数数组nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

【输入输出实例】

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

【算法思路】

方法一：

利用二分查找来找nums中第一个target的位置start(即返回left)，若没找到target则返回比target大的最近数的位置(可能出界)。再利用二分查找来找nums中第一个target + 1的位置end。

• 若在找start时就没找到target，则直接返回{-1, -1}；
• 若找到target，返回{start, end}。

方法二：

直接用二分查找来找target：

• 若没找到，则直接返回{-1, -1}；
• 若找到，则向两边扩展找target的区间，直到两边都找到不为target的数，那么边界为{left+1, right-1}。

【算法描述】

//方法一：直接用二分查找来找target的区间[start, end]，再返回{start, end}
vector<int> searchRange(vector<int>& nums, int target)
{
    int left = getleftBorder(nums, target);
    int right = getleftBorder(nums, target + 1);
    if(left == right)
    {
        return {-1, -1};
    }
    else
    {
        return {left, right-1};
    }
}
//利用二分查找来找nums中第一个target的位置，若无target则返回比target大的最近数的位置
int getleftBorder(vector<int>& nums, int target)
{
    int left = 0;    //左指针
    int right = nums.size() - 1;    //右指针
    while(left <= right)
    {
        int mid = (left + right) / 2;
        if(nums[mid] < target)
        {
            left = mid + 1;  //范围缩小到 [mid+1, right]
        }
        else
        {
            right = mid - 1;  //范围缩小到 [left, mid-1]
        }
    }
    return left;
}

//方法二：先用二分查找找target，找到后再向两边扩展找target的区间，直到两边都找到不为target的数
vector<int> searchRange(vector<int>& nums, int target) 
{
    int left = 0;    //左指针
    int right = nums.size() - 1;    //右指针
    int index = -1;
    //二分查找来找target
    while(left <= right)
    {
        int mid = (left + right) / 2;
        if(target == nums[mid])   //找到目标值后记录其下标位置
        {
            index = mid;
            break;
        }
        else if(nums[mid] > target)
        {
            right = mid - 1;
        }
        else
        {
            left = mid + 1;
        }
    }
    if(index == -1)  //没找到target
    {
        return {-1, -1};
    }
    else  //找到target，利用left和right向两边扩展
    {
        left = index - 1;
        right = index + 1;
        //在不超过边界的情况下，找target的区间
        while(left >= 0 && nums[left] == target)
        {
            left--;  //左开区间
        }
        while(right < nums.size() && nums[right] == target)
        {
            right++;  //右开区间
        }
        return {left+1, right-1};
    }
}

【知识点】

利用二分查找来找nums中第一个target的位置，若无target则返回比target大的最近数的位置。

int getleftBorder(vector<int>& nums, int target)
{
    int left = 0;    //左指针
    int right = nums.size() - 1;    //右指针
    while(left <= right)
    {
        int mid = (left + right) / 2;
        if(nums[mid] < target)
        {
            left = mid + 1;  //范围缩小到 [mid+1, right]
        }
        else
        {
            right = mid - 1;  //范围缩小到 [left, mid-1]
        }
    }
    return left;
}

搜索插入位置

【题目描述】

给定一个排序数组nums和一个目标值target，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

nums 为 无重复元素 的 升序 排列数组。请必须使用时间复杂度为 O(log n) 的算法。

【输入输出实例】

示例 1:

输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:

输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:

输入: nums = [1,3,5,6], target = 7
输出: 4

【算法思路】

不断用二分法逼近查找第一个大于等于target 的下标。利用二分查找来找nums中第一个target的位置，若无target则返回比target大的最近数的位置。

【算法描述】

//用二分法逼近查找第一个大于等于target的下标(可能出界)
int searchInsert(vector<int>& nums, int target) 
{
    int left = 0;   //左指针
    int right = nums.size() - 1;   //右指针
    while(left <= right)
    {
        int mid = (left + right) / 2;
        if(nums[mid] < target)
        {
            left = mid + 1;  //范围缩小到[mid+1, right]
        }
        else
        {
            right = mid - 1;  //范围缩小到[left, mid-1]
        }
    }
    return left;  //返回target下标或比target大的最近数下标(可能出界)
}

【知识点】

用二分法逼近查找排序数组nums中的第一个大于等于target 的下标(可能出界)。

与普通二分查找类似，但是少了if(nums[mid] == target)的判断，因为要找的是第一个target 的下标，不能随便找到一个target 就返回。所以不能有那个条件，要采取区间逼近的方法来做。即循环为：

if(nums[mid] < target)
{
	left = mid + 1;  //范围缩小到[mid+1, right]
}
else
{
	right = mid - 1;  //范围缩小到[left, mid-1]
}

最后循环完后，left就是第一个大于等于target 的下标。若数组中没有target，则left为比target大的最近数的位置。

Pow(x,n)

【题目描述】

实现 pow(x, n)，即计算 x 的整数 n 次幂函数（即xⁿ ）。

【输入输出实例】

示例 1：

输入：x = 2.00000, n = 10
输出：1024.00000

示例 2：

输入：x = 2.10000, n = 3
输出：9.26100

示例 3：

输入：x = 2.00000, n = -2
输出：0.25000

【算法思路】

使用折半计算，每次把 n 缩小一半，这样 n 最终会缩小到 0，任何数的 0 次方都为1，这时候我们再往回乘，如果此时n是偶数，直接把上次得到的值算个平方返回即可，如果是奇数，则还需要乘上个 x 的值。

xⁿ = x^n/2 * x^n/2 = (x²) ^n/2，令 n/2 为整数，则分为奇偶两种情况（设向下取整除法符号为 “//” ）：

观察发现，当 n 为奇数时，二分后会多出一项 x 。

还有一点需要引起我们的注意的是 n 有可能为负数，对于 n 是负数的情况，我们可以先用其绝对值计算出一个结果再取其倒数即可。我们让 i 初始化为 n，然后看 i 是否是 2 的倍数，是的话 x 乘以自己，否则 result 乘以 x，i 每次循环缩小一半，直到为 0 停止循环。最后看 n 的正负，如果为负，返回其倒数。

【算法描述】

double myPow(double x, int n)
{
   double result = 1.0;  //存放最后结果
   for(int i = n; i != 0; i /= 2)
   {
       if(i % 2 != 0)  //如果i是奇数，将一个x先乘给result
       {
           result *= x;
       }
       x *= x;  //i每次除2，x每次平方
   }
   return (n >= 0) ? result : 1/result;  //若n为负，返回其倒数
}

插入区间

【题目描述】

给你一个 无重叠的 *，*按照区间起始端点排序的区间列表。在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。

【输入输出实例】

示例 1：

输入：intervals = [[1,3],[6,9]], newInterval = [2,5]
输出：[[1,5],[6,9]]

示例 2：

输入：intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出：[[1,2],[3,10],[12,16]]

示例 3：

输入：intervals = [], newInterval = [5,7]
输出：[[5,7]]

示例 4：

输入：intervals = [[1,5]], newInterval = [2,3]
输出：[[1,5]]

示例 5：

输入：intervals = [[1,5]], newInterval = [2,7]
输出：[[1,7]]

【算法思路】

利用二分插入，将newInterval按顺序插入到intervals中，保证intervals还是根据intervals[i][0]升序排列，然后用56、合并区间的代码就可以。

【算法描述】

vector<vector<int>> insert(vector<vector<int>>& intervals, vector<int>& newInterval)
{
    //利用二分插入，将newInterval插入到intervals中，保证intervals还是根据intervals[i][0]升序排列
    int left = 0;   
    int right = intervals.size() - 1;
    while(left <= right)  //查找排序数组中的第一个大于等于target的下标（left）
    {
        int mid = (left + right) / 2;
        if(intervals[mid][0] < newInterval[0])
        {
            left = mid + 1;
        }
        else
        {
            right = mid - 1;
        }
    }
    intervals.insert(intervals.begin() + left, newInterval);  //将其插入适合位置
    return merge(intervals);   //利用 56、合并区间 的代码（去掉sort排序，因为intervals已经是升序的）
}
//合并区间：给定若干个区间的集合，合并所有重叠的区间并返回
vector<vector<int>> merge(vector<vector<int>>& intervals) {
    int len = intervals.size();
    vector<vector<int>> result;    //存放最后不重叠的区间数组
    for(int i = 0; i < len; i++)    //遍历各区间
    {
        //以当前区间intervals[i]作为 区间起点 和 区间终点
        int start = intervals[i][0];    //区间起点
        int end = intervals[i][1];    //区间终点
        //开始往后寻找是否可以更新区间终点end，如果后续的区间起点比end还小，说明区间重叠，可以归并到一起
        while(i < len - 1 && intervals[i+1][0] <= end)   
        {
            end = max(end, intervals[i+1][1]);  //更新更大的区间终点，注意要取最大值，防止前面的区间包含于后面的区间，例如[[1,4],[2,3]]
            i++;
        }
        result.push_back({start, end});   //将不重叠的区间放入result
    }
    return result;
}

x的平方根

【题目描述】

给你一个非负整数 x ，计算并返回 x 的算术平方根 。

由于返回类型是整数，结果只保留整数部分 ，小数部分将被舍去 。

注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

【输入输出实例】

示例 1：

输入：x = 4
输出：2

示例 2：

输入：x = 8
输出：2 （8 的算术平方根是 2.82842…, 由于返回类型是整数，小数部分将被舍去）

【算法思路】

方法一：顺序查找

• 从头开始遍历查找，找最后一个 其平方小于x 的数。用x / i < i判断而不是i * i > x，是因为防止溢出。

方法二：二分查找

• 由于 x 平方根的整数部分 ans 是满足 k² ≤ x 的最大 k 值，因此我们可以对 k 进行二分查找，从而得到答案。设置二分查找的下界为 0，上界可以设定为 x。在二分查找的每一步中，我们只需要比较中间元素 mid 的平方与 x 的大小关系，并通过比较的结果调整上下界的范围，最终找出最后一个小于等于目标值的数。

【算法描述】

//方法一：依次顺序查找
int mySqrt(int x) {
    for(int i = 1; i <= x; i++)    //从头开始顺序查找
    {
        if(x / i < i)    //不用i * i > x判断是因为防止溢出
        {
            return i-1;    //找到最后一个数的平方小于x，即为答案
        }
    }
    return x;
}

//方法二：二分查找
int mySqrt(int x) {
    int low = 0;
    int high = x;
    while(low <= high)    //找最后一个小于等于target的数
    {
        long mid = (low + high) / 2;    //用long类型，防止mid * mid溢出
        if(mid * mid > x)
        {
            high = mid - 1;
        }
        else
        {
            low = mid + 1;
        }
    }
    return high;
}

【知识点】

二分查找：

• 找第一个大于等于 target 的数(可能会越上界)： （循环完后 low 就是第一个大于等于target 的下标）

while(low <= high)    //找第一个大于等于target的数
{
    long mid = (low + high) / 2;    //用long类型，防止mid * mid溢出
    if(mid * mid < x)
    {
        low = mid + 1;
    }
    else
    {
        high = mid - 1;
    }
}

• 找最后一个小于等于target的数(可能会越下界)： （循环完后 high 就是最后一个小于等于target 的下标）

while(low <= high)    //找最后一个小于等于target的数
{
    long mid = (low + high) / 2;    //用long类型，防止mid * mid溢出
    if(mid * mid > x)
    {
        high = mid - 1;
    }
    else
    {
        low = mid + 1;
    }
}

搜索二维矩阵

【题目描述】

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

• 每行中的整数从左到右按升序排列；
• 每行的第一个整数大于前一行的最后一个整数。

【输入输出实例】

示例 1：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true

示例 2：

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

【算法思路】

解法一

由于每行的第一个元素大于前一行的最后一个元素，且每行元素是升序的，所以每行的第一个元素大于前一行的第一个元素，因此矩阵第一列的元素是升序的。

• 对矩阵的第一列元素进行二分逼近查找，找到最后一个小于等于目标值的元素；
• 然后在该元素所在行中二分查找目标值是否存在。

解法二

将二维矩阵当作一维数组，排列顺序为从左到右，从上到下，直接进行二分查找，对每次求得mid的结果进行坐标转换：

int i = mid / n;
int j = mid % n;

【算法描述】

// 解法一：两次二分查找
bool searchMatrix(vector<vector<int>>& matrix, int target)
{
    int m = matrix.size();    //行数
    int n = matrix[0].size();    //列数
    //按每行第一个元素进行二分查找，找最后一个小于等于目标值的元素
    int low = 0;
    int high = m - 1;
    while(low <= high)
    {
        int mid = (low + high) / 2;
        if(target < matrix[mid][0])
        {
            high = mid - 1;
        }
        else
        {
            low = mid + 1;
        }
    }
    if(high == -1)    //一个小于等于目标值的都没有
    {
        return false;
    }
    //找到所在行，对所在行进行二分查找，找目标值target
    int left = 0;
    int right = n - 1;
    while(left <= right)
    {
        int mid = (left + right) / 2;
        if(target == matrix[high][mid])
        {
            return true;
        }
        else if(target > matrix[high][mid])
        {
            left = mid + 1;
        }
        else
        {
            right = mid - 1;
        }
    }
    return false;
}

// 解法二：直接二分查找（推荐）
bool searchMatrix(vector<vector<int>>& matrix, int target) {
    int m = matrix.size();    	//行数
    int n = matrix[0].size();  	//列数
    int left = 0;
    int right = m * n - 1;
    while(left <= right) {
        int mid = (left + right) / 2;
        int i = mid / n;		// 将mid转换为二维坐标
        int j = mid % n;
        if(target == matrix[i][j]) {
            return true;
        }
        else if(target > matrix[i][j]) {
            left = mid + 1;
        }
        else {
            right = mid - 1;
        }
    }
    return false;
}

---

恭喜你全部读完啦！古人云：温故而知新。赶紧收藏关注起来，用之前再翻一翻吧~

---

📣推荐阅读

C/C++后端开发面试总结：点击进入 后端开发面经 关注走一波

C++重点知识：点击进入 C++重点知识 关注走一波

力扣（leetcode）题目分类：点击进入 leetcode题目分类 关注走一波