LeetCode[4]：寻找两个正序数组的中位数

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：
输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例2：
输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

示例 3：
输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

示例 4：
输入：nums1 = [], nums2 = [1]
输出：1.00000

示例 5：
输入：nums1 = [2], nums2 = []
输出：2.00000

Related Topics
数组
二分查找
分治

方法一

想到的第一种方法也是，简单粗暴，直接合并两个数组，排序后取中位数

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        double median = 0;
        ArrayList<Integer> list = new ArrayList<>();
        for (int i = 0; i < nums1.length; i++) {
            list.add(nums1[i]);
        }
        for (int i = 0; i < nums2.length; i++) {
            list.add(nums2[i]);
        }
        Collections.sort(list);
        int sumLength = nums1.length + nums2.length;
        int index = sumLength / 2;
        if (sumLength % 2 == 0) {//偶数个数
            median = (list.get(index) + list.get(index - 1)) / 2.0;
        }else {
            median = list.get(index);
        }
        return median;
    }
}

这种方法最简单，但是时间复杂度最后还是到了O(m+n)

方法二

也是题目要求的一个题目，要求时间复杂度减低到O(log(m+n))，那么就要使用到二分法
之前也听说过二分法，那时候说什么一段电线断了，然后如何快速找到断点：给电线通电，然后取中间，看能不能收到电信号，收到不电信号的一端就是断点处，这样一下就排除了一半的电线距离……说是这么说，但是这里突然叫你用，不知道如何用上……

这里引用一下LeetCode中大佬的讲解:
题目是求中位数，其实就是求第 k 小数的一种特殊情况，而求第 k 小数有一种算法。我们一次遍历就相当于去掉不可能是中位数的一个值，也就是一个一个排除。由于数列是有序的，其实我们完全可以一半儿一半儿的排除。假设我们要找第 k 小数，我们可以每次循环排除掉 k/2 个数。看下边一个例子。

假设我们要找第 7 小的数字。

我们比较两个数组的第 k/2 个数字，如果 k 是奇数，向下取整。也就是比较第 3 个数字，上边数组中的 4 和下边数组中的 3，如果哪个小，就表明该数组的前 k/2 个数字都不是第 k 小数字，所以可以排除。也就是 1，2，3 这三个数字不可能是第 7 小的数字，我们可以把它排除掉。将 1349 和 45678910 两个数组作为新的数组进行比较。

更一般的情况 A[1] ，A[2] ，A[3]，A[k/2] … ，B[1]，B[2]，B[3]，B[k/2] … ，如果 A[k/2]<B[k/2] ，那么A[1]，A[2]，A[3]，A[k/2]都不可能是第 k 小的数字。

A 数组中比 A[k/2] 小的数有 k/2-1 个，B 数组中，B[k/2] 比 A[k/2] 小，假设 B[k/2] 前边的数字都比 A[k/2] 小，也只有 k/2-1 个，所以比 A[k/2] 小的数字最多有 k/1-1+k/2-1=k-2个，所以 A[k/2] 最多是第 k-1 小的数。而比 A[k/2] 小的数更不可能是第 k 小的数了，所以可以把它们排除。

橙色的部分表示已经去掉的数字。

由于我们已经排除掉了 3 个数字，就是这 3 个数字一定在最前边，所以在两个新数组中，我们只需要找第 7 - 3 = 4 小的数字就可以了，也就是 k = 4。此时两个数组，比较第 2 个数字，3 < 5，所以我们可以把小的那个数组中的 1 ，3 排除掉了。

我们又排除掉 2 个数字，所以现在找第 4 - 2 = 2 小的数字就可以了。此时比较两个数组中的第 k / 2 = 1 个数，4 == 4，怎么办呢？由于两个数相等，所以我们无论去掉哪个数组中的都行，因为去掉 1 个总会保留 1 个的，所以没有影响。为了统一，我们就假设 4 > 4 吧，所以此时将下边的 4 去掉。

由于又去掉 1 个数字，此时我们要找第 1 小的数字，所以只需判断两个数组中第一个数字哪个小就可以了，也就是 4。

所以第 7 小的数字是 4。

我们每次都是取 k/2 的数进行比较，有时候可能会遇到数组长度小于 k/2的时候。

此时 k / 2 等于 3，而上边的数组长度是 2，我们此时将箭头指向它的末尾就可以了。这样的话，由于 2 < 3，所以就会导致上边的数组 1，2 都被排除。造成下边的情况。

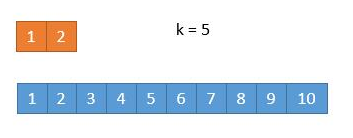
由于 2 个元素被排除，所以此时 k = 5，又由于上边的数组已经空了，我们只需要返回下边的数组的第 5 个数字就可以了。

从上边可以看到，无论是找第奇数个还是第偶数个数字，对我们的算法并没有影响，而且在算法进行中，k 的值都有可能从奇数变为偶数，最终都会变为 1 或者由于一个数组空了，直接返回结果。

所以我们采用递归的思路，为了防止数组长度小于 k/2，所以每次比较 min(k/2，len(数组) 对应的数字，把小的那个对应的数组的数字排除，将两个新数组进入递归，并且 k 要减去排除的数字的个数。递归出口就是当 k=1 或者其中一个数字长度是 0 了。

上代码：

class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        //1、合并奇偶数的情况,无论奇数还是偶数，都取两个数‘中位数’，然后/2
        /* 例如偶数6和奇数7
        对于偶数6：(6+1)/2==3,(6+2)/2==4，(第三个数+第四个数)/2正好是长度为6的数组的中位数
        对于奇数7：(7+1)/2==4,(7+2)/2==4，(第四个数+第四个数)/2也正好是长度为7的数组的中位数
         */
        int len1 = nums1.length;
        int len2 = nums2.length;
        int left = (len1 + len2 + 1) / 2;
        int right = (len1 + len2 + 2) / 2;
        return (dichotomy(nums1, 0, len1 - 1, nums2, 0, len2 - 1, left) + dichotomy(nums1, 0, len1 - 1, nums2, 0, len2 - 1, right)) * 0.5;
    }

    /**
     * @param nums1 子数组1
     * @param nums2 子数组2
     * @param k 第k小的数
     * @return 要找的第k小的数的值
     */
    public int dichotomy(int[] nums1, int start1,int end1, int[] nums2, int start2,int end2, int k) {
        int len1 = end1 - start1 + 1;//计算两个数组的剩余长度
        int len2 = end2 - start2 + 1;
        //让len1的长度小于len2，这样就能保证有数组空了，也一定是num1，减少了几个if
        //这个递归直接调用自己改变参数位置的方法也是学到了，我第一想的是交换num1，num2的值这种操作
        if (len1>len2) return dichotomy(nums2, start2, end2, nums1, start1, end1, k);
        if (len1==0) return nums2[start2 + k - 1];
        if (k==1) return Math.min(nums1[start1], nums2[start2]);

        //start要么全部排除掉，要么就只会排除掉k/2
        //并且谁小就会排除谁，巧妙的用min函数取代了if结构
        int i = start1 + Math.min(len1, k / 2) - 1;
        int j = start2 + Math.min(len2, k / 2) - 1;

        //判断start移动后所在索引数字的大小，决定保留谁的移动，减小查找范围
        if (nums1[i] > nums2[j]) {
            return dichotomy(nums1, start1, end1, nums2, j + 1, end2, k - (j + 1 - start2));
        } else {
            return dichotomy(nums1, i + 1, end1, nums2, start2, end2, k - (i + 1 - start1));
        }
    }

}

理解思路，和写出简介的代码，也还是有很多差距的，我靠自己能力写的时候，写了很多很多if，然后还会有很多情况遗漏，然后是参考着大佬的代码跟着理解写了一遍。也认识到自己还有很长很长的路要走…
大佬貌似擅长把多种复杂的情况尽量统一成少数的情况，例如上面奇偶数的问题、受益良多。