代码随想录：单调栈4-5

42.接雨水

题目

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。 

示例 2：

输入：height = [4,2,0,3,2,5]
输出：9

代码（单调栈）

class Solution {
    public int trap(int[] height) {

        //雨水的关键是找凹槽，凹槽是栈顶的mid，右边柱子是当前更大的元素，左边的柱子是栈顶下面的元素
        //单调递减栈：寻找右边第一个更大的元素
        Stack<Integer> stack = new Stack<>();
        //栈中放的是元素下标，第一个元素入栈,高度=height[0]
        stack.push(0);

        int sum = 0;  //初始雨水

        //i是当前元素下标，height[i]是当前元素高度
        for(int i=1; i < height.length; i++){
            //当前元素高度 < 栈顶元素高度
            if(height[i] < height[stack.peek()]){
                stack.push(i);  //当前元素下标入栈
            }
            //当前元素高度 = 栈顶元素高度
            else if(height[i] == height[stack.peek()]){
                //因为栈顶高度和当前元素高度，栈顶的柱子肯定没有雨水
                stack.pop();  //栈顶元素入栈
                stack.push(i);  //当前元素下标入栈
            }
            //当前元素高度 > 栈顶元素高度,出现凹槽
            else{
                //只要当前元素高度比栈顶元素高度大，循环处理所有凹槽
                while(!stack.isEmpty() && height[i] > height[stack.peek()]){
                    int mid = stack.pop();  //凹槽下标

                    //mid出栈后，如果栈为空，说明mid左边是空的，没有雨水,[1],mid=1，1出栈就行
                    //mid出栈后，如果栈非空，说明mid左边不空，有雨水，需要计算雨水量
                    if(!stack.isEmpty()){
                        int left = stack.peek();  //凹槽左边下标
                        //mid凹槽的雨水高度 = 左右高度最小值-凹槽高度
                        int h = Math.min(height[i], height[left]) - height[mid];
                        //mid凹槽的雨水宽度
                        int w = i - left - 1;  //这里要写- left - 1，不能写-mid，[4,2,0,3,2,5]画个图就知道了
                        int area = h * w;  //mid凹槽雨水量
                        sum += area;   
                    }
                }
                stack.push(i);//当前元素下标入栈
            }
        }
        return sum;  //返回总雨水量
    }
}

代码（双指针）

class Solution {
    public int trap(int[] height) {
        int[] left = new int[height.length];
        int[] right = new int[height.length];

        left[0] = height[0];
        for(int i=1; i < height.length; i++){
            left[i] = Math.max(height[i], left[i-1]);
        }

        right[height.length-1] = height[height.length -1];
        for(int i=height.length-2; i >= 0; i--){
            right[i] = Math.max(height[i], right[i+1]);
        }

        int res = 0;
        for(int i=0; i < height.length; i++){
            int area = Math.min(left[i], right[i]) - height[i];
            res += area;
        }
        return res;
    }
}

84.柱状图中最大的矩形

题目

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

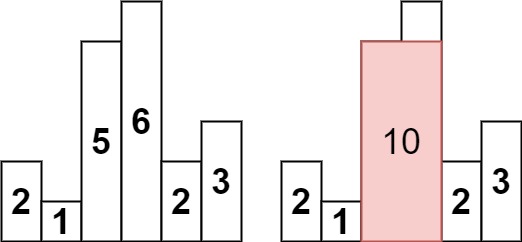
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

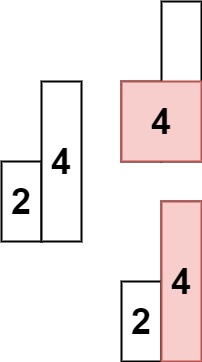
输入： heights = [2,4]
输出： 4

代码

class Solution {
    public int largestRectangleArea(int[] heights) {
        //关键是找变小的元素，变小了，就把前面的矩形面积计算出来

        //扩容，头尾加元素0
        int[] newHeights = new int[heights.length + 2];
        //头部加0，防止出现[8,6,4,2]递减序列算出来是0
        newHeights[0] = 0;
        //尾部加0，防止出现[2,4,6,8]递增序列算出来是0
        newHeights[newHeights.length - 1] = 0;
        //数组copy
        for(int i=0; i < heights.length; i++){
            newHeights[i+1] = heights[i];
        }

        int res = 0; //初始最大面积
        //单调栈，找右边第一个更小的元素
        Stack<Integer> stack = new Stack<>();
        //第一个元素下标入栈
        stack.push(0);  

        for(int i=1; i < newHeights.length; i++){
            //当前元素高度 > 栈顶元素高度
            //举例：[1,5,6]持续入栈
            if(newHeights[i] > newHeights[stack.peek()]){
                stack.push(i);  //下标入栈
            }
            //当前元素高度 = 栈顶元素高度
            //举例：[1,5,5,6]，当前元素=2,最大值会在第一个5取到，5不用出栈
            else if(newHeights[i] == newHeights[stack.peek()]){
                stack.push(i);  //下标入栈
            }
            //当前元素高度 < 栈顶元素高度
            else{
                //[1,5,6],当前元素=2，要出栈循环计算矩形大小
                while(!stack.isEmpty() && newHeights[i] < newHeights[stack.peek()]){
                    int mid = stack.pop();  //6的下标
                    if(!stack.isEmpty()){
                        int left = stack.peek();  //5的下标
                        int h = newHeights[mid]; //高度是6
                        int w = i - left - 1;  //宽度是1
                        int area = h * w; //面积是6
                        res = Math.max(res, area);  //更新最大矩形面积
                    }
                }
                stack.push(i);
            }
        }
        return res;
    }
}