本文是Java入门算法系列的贪心篇，适合初学者。通过生动的例题，如花朵、糖果、饼干和股票问题，讲解贪心算法的基本思想和应用场景。贪心算法在解决局部最优解能导出整体最优解的问题时非常有效，例如在分发糖果、分配饼干和买卖股票等问题中。学习贪心算法有助于提升编程能力和面试竞争力。
本专栏已参加蓄力计划，感谢读者支持
往期文章
一. Java入门算法（贪心篇）丨蓄力计划
二. Java入门算法（暴力篇）丨蓄力计划
三. Java入门算法（排序篇）丨蓄力计划
四. Java入门算法（递归篇）丨蓄力计划
五. Java入门算法（双指针篇）丨蓄力计划
六. Java入门算法（数据结构篇）丨蓄力计划
七. Java入门算法（滑动窗口篇）丨蓄力计划
你好，我是Ayingzz，Ayi是我的名字，ing进行时代表我很有动力，zz提醒我按时睡觉 ~
- 篇幅短小精悍，适合初学者反复咀嚼：此专栏的文章并不是一系列大而全的整理文章，而是一系列简明扼要的算法入门讲解文章，篇幅短而内容精，有利于初学者针对一种或多种算法快速入门。
- 例题简单易懂，让你印象深刻：引入精选LeetCode简易算法例题，通过生动形象的讲解对其思路进行简明剖析，更容易上手并掌握。
- 涉及算法种类广：双指针、递归、排序、贪心、分治、动态规划、滑动窗口、DFS...各类基础算法收揽其中。
为什么要学算法？
对于所有的Problems-Solving的过程都可以理解为算法，程序员对算法或多或少都有着一些复杂的情感，为什么一定要学算法？
- "程序 = 数据结构 + 算法"。这个公式相信已经耳濡目染，目前在各大厂的面试里，对基础算法的考察的比重逐年增加，只写会某种语言的工程代码显然并不太够，大部分面试官会优先考虑掌握算法的面试者。在现实开发里，仅使用一些简单的算法就可以快读优化各种繁杂的工程代码，降低时间复杂度与工程运行速度，提升用户体验。
- 对算法的热爱。作为程序员或多或少对算法都有着某种情感上的执着与偏爱，如果你还是学生，想参与各类的竞赛，那么入门算法即是数学建模、软件开发、算法等各类竞赛的敲门砖，选手的动力就是对算法的追求与热爱，类似的有ACM、蓝桥杯等。
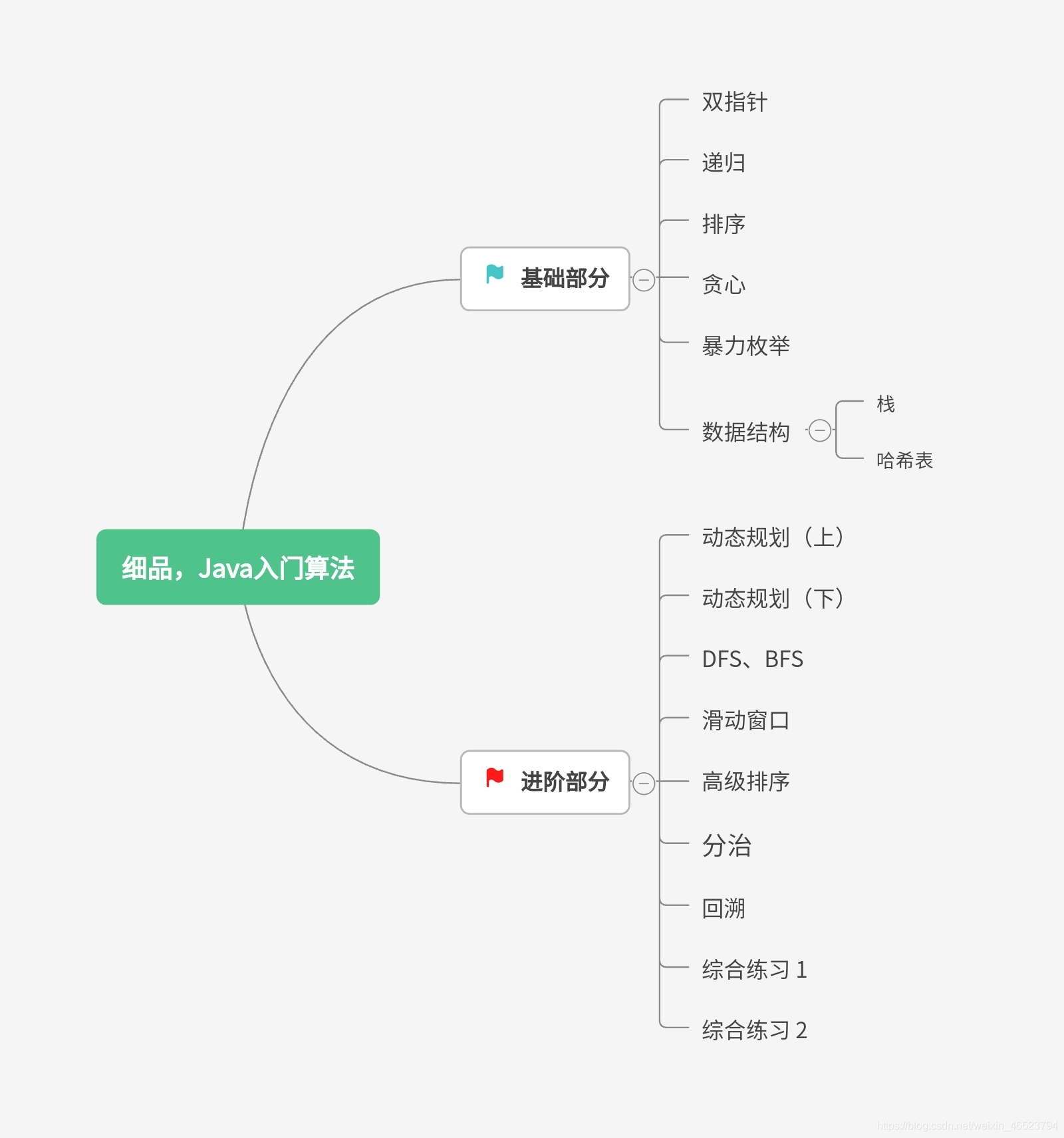
专栏思路和内容大纲
基础部分：
- 双指针：巧用双指针、三指针完成搜索以及其他算法功能；
- 递归：递归是算法的敲门砖，大部分算法中都包含递归；
- 排序：基础入门排序算法，包括选择、插入、冒泡排序；
- 贪心：贪心选择性质、最优子问题讲解；
- 暴力枚举：常见的暴力枚举题目讲解，铺垫之后的优化；
- 数据结构：包括栈、哈希表等。
进阶部分：
- 动态规划：一张表可以解决的问题，进阶版递归；
- DFS与BFS：深度优先搜索、广度优先搜索；
- 滑动窗口：利用指针或数组维护特定区间的移动；
- 高级排序：排序用时短的高级排序，包括快速排序、归并排序、堆排序等；
- 分治：分而治之，对原问题的切割子问题求解；
- 回溯：以深度优先方式配合状态变量系统搜索问题解的算法。
适宜人群
- 对算法感兴趣的初学者
- 想加强算法基本功的读者
~
前言
贪心算法是入门算法之一，它在百度百科上是这样解释的。
贪心算法的使用条件有两个：
- 贪心选择性质
一个问题的整体最优解可以通过一系列局部最优解的选择达到，并且每次的选择可以依赖以前作出的选择，但不依赖于后面要作出的选择，这就是贪心选择性质。 - 最优子结构性质
当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。问题的最优子结构性质是该问题可用贪心法求解的关键所在。在实际应用中，至于什么问题具有什么样的贪心选择性质是不确定的，需要具体问题具体分析。
（本篇内容）
花朵 Flower
-
LeetCode题目描述：
605.种花问题（Easy）
- 假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。
- 给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。
示例
输入：flowerbed = [1,0,0,0,1], n = 1
输出：true
------------------------------------
输入：flowerbed = [1,0,0,0,1], n = 2
输出：false
思路：
- 每次只考虑局部的最优解，也就是考虑具体一个地块能不能种花；
- 结合1，花坛从左往右一格一格看过去，若某个格子可以种花，则计入当前可种花总数；若不可以种花，则丢弃，继续下一格；
- 能否种花取决于左右格子是否为空地，题目给出的花坛数组中，种花的右侧一定是空地，所以我们可以每一次跳2格（i += 2）；
- 基于3的种花条件：当前地块为空地 且 右侧为空地，或者，当前地块为空地 且 为花坛右边界；
- 计数方式：当某个空地的考虑结果是可种花时，将n - 1；
- 结果判断：若n为零或者负值，证明此花坛可种花数大于n，返回true，否则返回false。
贪心策略的使用：
class Solution {
public boolean canPlaceFlowers(int[] flowerbed, int n) {
int L = flowerbed.length;
for (int i = 0; i < L; i += 2) {
if (flowerbed[i] == 0) {
if (i == L - 1 || flowerbed[i + 1] == 0) {
n--;
}else{
i++;
}
}
}
return n <= 0;
}
}
糖果 Candy
LeetCode题目描述：135. 分发糖果（Hard）
老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。
-
你需要按照以下要求，帮助老师给这些孩子分发糖果：
- 每个孩子至少分配到 1 个糖果。
- 评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果。
- 那么这样下来，老师至少需要准备多少颗糖果呢？
示例
输入：[1,0,2]
输出：5
解释：你可以分别给这三个孩子分发 2、1、2 颗糖果。
-----------------------------------------------------
输入：[1,2,2]
输出：4
解释：你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果，这已满足上述两个条件。
思路：
- 因为每个孩子至少被分配到1个糖果，所以初始化数组元素为1；
- 题目的难点是评分更高的孩子必须比他两侧的邻位孩子获得更多的糖果，我们可以分开两次考虑，一次只考虑每个孩子与他右侧的孩子的分数关系，一次只考虑每个孩子与他左侧孩子的分数关系。按照关系，修改每个孩子得到的糖果数量。
- 需要注意的是，因为第一次从左往右遍历时数组已经修改，所以在第二次从右往左的遍历里，不仅要考虑每个孩子与他左侧孩子的分数关系，还要考虑两个孩子已经得到的糖果数量关系。
- 最后，只需将修改的数组做累加，即可求出至少需要准备的糖果数量。
贪心策略的使用：
class Solution {
public static int candy(int[] ratings) {
int[] candy = new int[ratings.length];
// 每个孩子至少有一个糖果，初始化数组元素为1
Arrays.fill(candy, 1);
// 从左往右，每次考虑左边孩子评分比右边孩子评分高的情况
for (int i = 0; i < ratings.length - 1; ++i) {
if (ratings[i + 1] > ratings[i]) {
candy[i + 1] = candy[i] + 1;
}
}
// 从右往左，每次考虑右边孩子评分比左边孩子评分高的情况
for (int i = ratings.length - 1; i > 0; --i) {
if (ratings[i - 1] > ratings[i] && candy[i - 1] <= candy[i]) {
candy[i - 1] = candy[i] + 1;
}
}
// 答案数组求和
int min_candy_sum = 0;
for (int x : candy) {
min_candy_sum += x;
}
return min_candy_sum;
}
}
饼干 Cookie
-
LeetCode题目描述：
455. 分发饼干（Easy）
- 假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。
- 对每个孩子 i，都有一个胃口值 g [ i ]，这是能让孩子们满足胃口的饼干的最小尺寸；
- 每块饼干 j，都有一个尺寸 s [ j ] 。如果 s [ j ] >= g [ i ]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。
- 你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。
示例
输入: g = [1,2,3], s = [1,1]
输出: 1
解释:
你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。
虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。
所以你应该输出1。
---------------------------------------------------------------------
输入: g = [1,2], s = [1,2,3]
输出: 2
解释:
你有两个孩子和三块小饼干，2个孩子的胃口值分别是1,2。
你拥有的饼干数量和尺寸都足以让所有孩子满足。
所以你应该输出2.
思路：
- 贪心策略下，应先考虑胃口值最小的孩子，并把大于等于这个孩子饥饿度的、且大小最小的饼干分配给这个孩子。所以我们需要先将两个数组升序排序。
- 每次由当前孩子选择饼干，若能满足这个孩子，则轮到下一个孩子选择；不能满足，则还是这个孩子选择饼干，且考虑下一个大小更大的饼干。（饼干不能重复选择）
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int child = 0, cookie = 0;
while (child < g.length && cookie < s.length) {
// 如果能满足，则轮到下一个孩子选饼干
if (g[child] <= s[cookie]) {
++child;
}
++cookie;
}
// 轮流了多少个孩子，就是满足了的孩子的数量
return child;
}
}
股票 Stock
-
LeetCode题目描述：
122. 买卖股票的最佳时机 ll（Easy）
- 给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润，你可以多次买卖这一支股票。
*注：你必须在再次购买前出售掉之前的股票。
示例
输入: [7,1,5,3,6,4]
输出: 7
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 3 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5 -1 = 4 。随后，在第 4 天（股票价格 = 3）的时候买入，在第 5 天（股票价格 = 6）的时候卖出, 这笔交易所能获得利润 = 6 -3 = 3 。
输入: [1,2,3,4,5]
输出: 4
解释: 在第 1 天（股票价格 = 1）的时候买入，在第 5 天 （股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。
思路：
- 我们先只寻找买入的时间（也就是极小值 / 上升沿），找到后买入；
- 再只寻找卖出的时间（也就是极大值 / 下降沿），找到后卖出。
贪心策略的使用：
class Solution {
public int maxProfit(int[] prices) {
int ans = 0;
int n = prices.length;
if (n == 1) {
return 0;
}
for (int i = 0; i < n - 1; ++i) {
// 寻找极小值
while (i < n - 1 && prices[i] > prices[i + 1]) {
++i;
}
// 买入
ans -= prices[i];
// 寻找极大值
while (i < n - 1 && prices[i] < prices[i + 1]) {
++i;
}
// 卖出
ans += prices[i];
}
return ans;
}
}
（推荐练习）
\
加油站
- 在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。
- 你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。
- 如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。
跳跃游戏
- 给定一个非负整数数组 nums ，你最初位于数组的 第一个下标 。
- 数组中的每个元素代表你在该位置可以跳跃的最大长度。
- 判断你是否能够到达最后一个下标。
/
总的来说，具体问题具体分析，只要确定一个问题的局部最优解可以导致问题的整体最优解，那么即可以考虑选择贪心策略、分治或动态规划（下篇）解决。
若有不当欢迎指正。本专栏持续周更，预计7月结束
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
