LeetCode084：柱状图中最大的矩形

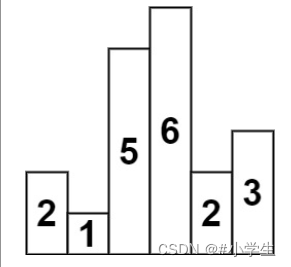
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

这题考的基础模型其实就是：在一维数组中对每一个数找到第一个比自己小的元素。这类“在一维数组中找第一个满足某种条件的数”的场景就是典型的单调栈应用场景。

思路：以第i根柱子为最矮柱子所能延伸的最大面积----->以第i根柱子为右边界，然后以pop后的stack[-1]为左边界，以第tmp根柱子高度为基准计算的最大面积。当我们找 i 左边第一个小于 heights[i] 如果 heights[i-1] >= heights[i] 其实就是和 heights[i-1] 左边第一个小于 heights[i-1] 一样。依次类推，右边同理
stack是单调递增的栈，所以栈顶元素最大，当栈顶元素stack[-1]碰到小于它的height[i]时，说明它碰到了它的右边界，此时将栈顶元素取出作为tmp，那么之后栈顶的元素stack[-1]一定小于tmp，因为stack是单调递增的，此时的stack[-1]就是tmp的左边界。

是以i 为中心，向左找第一个小于 heights[i] 的位置 left_i；向右找第一个小于于 heights[i] 的位置 right_i，即最大面积为 heights[i] * (right_i - left_i -1)

class Solution {
    public int largestRectangleArea(int[] heights) {
        if (heights.length == 0) return 0;
        int n = heights.length;
        int[] left_i = new int[n];
        int[] right_i = new int[n];
        left_i[0] = -1;
        right_i[n - 1] = n;
        int res = 0;
        for (int i = 1; i < n; i++) {
            int tmp = i - 1;
            while (tmp >= 0 && heights[tmp] >= heights[i]) tmp = left_i[tmp];
            left_i[i] = tmp;
        }
        for (int i = n - 2; i >= 0; i--) {
            int tmp = i + 1;
            while (tmp < n && heights[tmp] >= heights[i]) tmp = right_i[tmp];
            right_i[i] = tmp;
        }
        for (int i = 0; i < n; i++) res = Math.max(res, (right_i[i] - left_i[i] - 1) * heights[i]);
        return res;  
    }
}

数据初始化

栈求解的思路是：
1.先将题目给定的数组左右各添加一个元素0，为了方便确定原有数组中第一个元素和最后一个元素能不能继续扩张；

2.然后开始从左到右依次遍历数组中的元素，如果栈为空或者当前考察的新元素值比栈顶元素值大，表明以栈顶元素值为高的矩形面积暂不能确定，所以就将当前考察的新元素入栈。在这个条件下，栈中的元素值从栈底到栈顶是依次递增的；
如果栈不为空且当前考察的新元素值比栈顶元素值小，表明以栈顶元素值为高的矩形的面积是可以确定的了。该矩形的高就是栈顶元素值，其右侧边界就是当前考察的新元素，左侧边界是栈顶元素的前一个元素，因为，在上一步中我们知道栈中元素值从栈底到栈顶是依次递增的。 因此，矩形的宽是当前考察的元素索引与栈顶元素前一个元素的索引的差值减一。

这里需要注意的是，当栈顶元素出栈后，需要继续看当前考察的新元素值是否大于新的栈顶元素值，如果是，就继续将栈顶元素弹出，然后计算以其值为高的矩形面积，直到当前考察的新元素值大于栈顶元素值时，当前考察元素入栈。

最后，由于最终计算矩形面积时，是用两个柱子的索引来确定矩形宽度的。因此，栈中存储的应该是给定数组的索引。

public int largestRectangleArea(int[] heights) {
    // 初始化最终结果为0
    int res = 0;
    Stack<Integer> stack = new Stack<>();

    // 将给定的原数组左右各添加一个元素0
    int[] newHeights = new int[heights.length + 2];
    newHeights[0] = 0;
    newHeights[newHeights.length-1] = 0;
    for (int i = 1; i < heights.length + 1; i++) {
        newHeights[i] = heights[i - 1];
    }

    for (int i = 0; i < newHeights.length; i++) {
        // 如果栈不为空且当前考察的元素值小于栈顶元素值，
        // 则表示以栈顶元素值为高的矩形面积可以确定
        while (!stack.isEmpty() && newHeights[i] < newHeights[stack.peek()]) {
            // 弹出栈顶元素
            int cur = stack.pop();
            // 获取栈顶元素对应的高
            int curHeight = newHeights[cur];

            // 栈顶元素弹出后，新的栈顶元素就是其左侧边界
            int leftIndex = stack.peek();
            // 右侧边界是当前考察的索引
            int rightIndex = i;
            // 计算矩形宽度
            int curWidth = rightIndex - leftIndex - 1;

            // 计算面积
            res = Math.max(res, curWidth * curHeight);
        }
        
        // 当前考察索引入栈
        stack.push(i);
    }

    return res;
}