算法：全排列

全排列

编写一个函数求解某字符串中所有字符的排列（不包括重复）。
例如字符串“ABC”，它的全排列有：
ABC ACB BAC BCA CAB CBA

思路

全排列实际上只需要以下步骤：

1. 选择“老大”，即将字符串中的其中一个字符移至字符串最前面，当作此字符串的“老大”。
2. 在除了“老大”字符之外的字串中再选择一个“老大”。
3. 重复上述步骤，直到字串只有一个字符时，返回上一层，将“老大”更换成没有当过“老大”的字符。如子串中的字符都当过“老大”，则继续返回上一层。

过程

现在用图片进行举例，使用例子为字符串“ABC”。
第一步，选择老大，此时选择字符串的第一个字符当作老大，即“A”为字符串“ABC”的老大。这一个步骤可以理解为自己和自己进行交换位置。

第二步，在除了老大“A”之外的字串中再选择一个老大，在此时。字符串“BC”的老大为“B”。

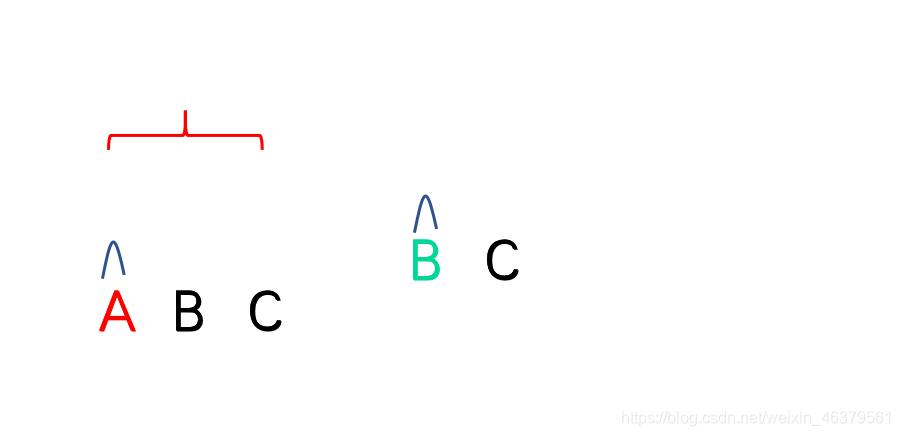
第三步，在除了老大“B”之外的字串中再选择一个老大。字符串“B”的老大为“C”。此时字串中只有一个字符，返回上一层，即“BC”字符串。
第四步，“BC”字符串中，“B”已经当过老大，所以这时将“C”移动到字符串第一个位置，让“C”当老大。“C”当老大时子串中只有一个字符“B”，遍历过后返回上一层。

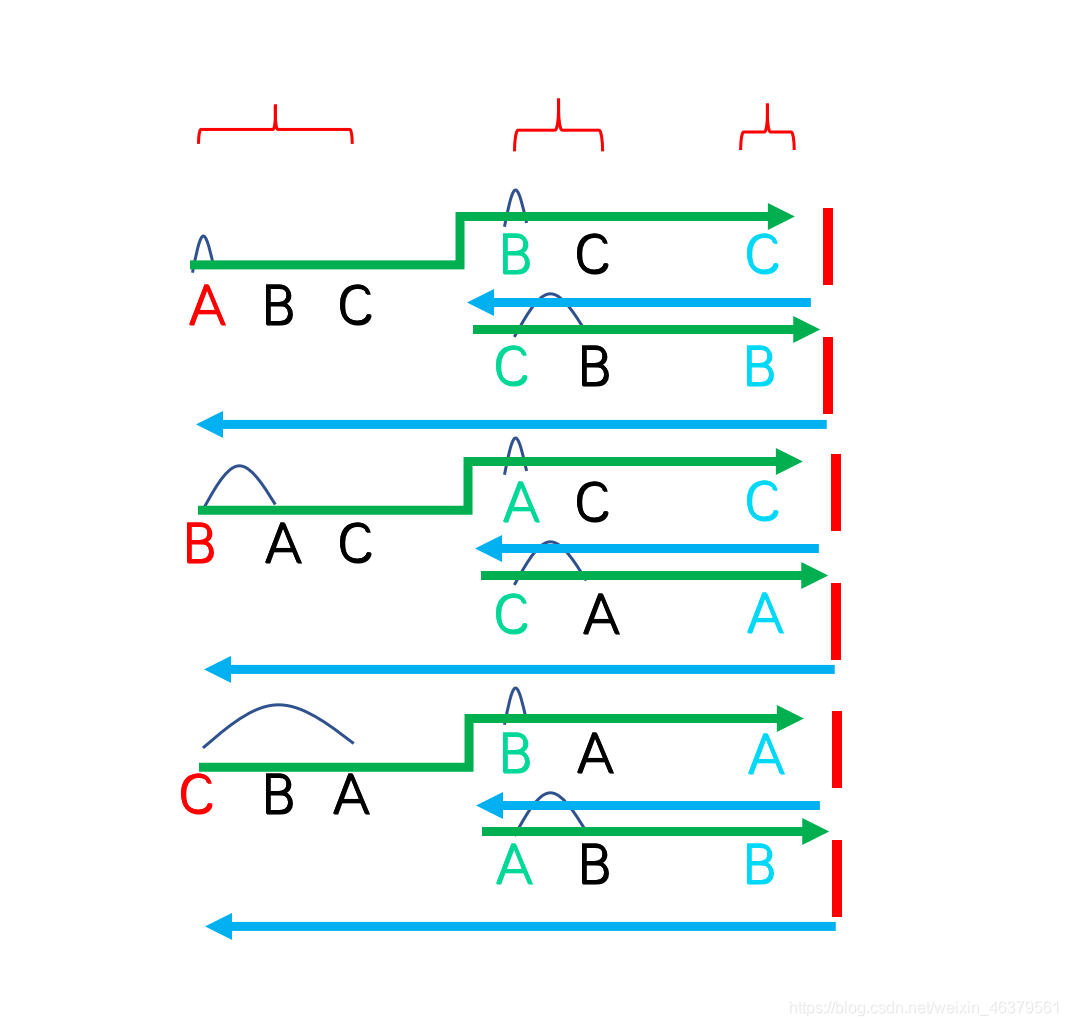
第五步，此时子串“BC”中，“B”和“C”都当过了老大，所以继续返回上一层。返回到字符串“ABC”。在上述步骤中，“ABC”中“A”当老大的情况都已经考虑完了，现在选择“B”当做“ABC”的老大，以此类推继续执行上述步骤，如图所示，当“ABC”中所有字符都当过一次老大，则全排列的所有情况就已经全部考虑到了。

代码

我们使用递归的方式来实现全排列。使用HashSet存放所有全排列的情况，代码如下：

public class FullPermutation1 {

    public static void main(String[] args) {
        String s = "AB";
        HashSet<String> set = new HashSet<>();
        //参数依次是存放排列的集合、字符串中第0个字符、字符串最后一个字符、字符串转换成字符数组
        Permutation1(set,0,s.length()  - 1,s.toCharArray());
        System.out.println(set.toString());
    }
    //start指针指向字符数组第0个位置，end指向最后一个位置
    private static void Permutation1(HashSet<String> set, int start, int end, char[] s) {
        //递归退出条件：当start指向end时，即数组遍历完成
        if(start == end){
            //将排列情况使用字符串添加进集合set
            set.add(new String(s));
        }
        else{
            for(int i = start;i <= end;i++){
                //第0个字符和第i个字符进行交换，即每个字符都要前移当一次老大
                swap(start,i,s);
                //递归调用，从start的下一个元素开始
                Permutation1(set,start + 1,end,s);
                //排列完此次情况后，将交换过的字符换回来，保证原本字符的顺序
                swap(start,i,s);
            }
        }
    }

    private static void swap(int start, int i,char[] s) {
        char t = s[start];
        s[start] = s[i];
        s[i] = t;
    }
}

运行结果如下：