本文深入探讨了二叉排序树的定义、插入、查找和删除操作，以及如何通过中序遍历保持有序性。同时，介绍了平衡二叉排序树的概念，特别是AVL树，强调了其在插入和删除时如何通过旋转操作保持平衡，确保高效查找。代码示例展示了Java实现的二叉排序树和AVL树的插入、删除过程。
PS：排序和查找是分不开的，排好序是为了更好地查找。
1、二叉排序树
（1）定义
二叉排序树：或者是一棵空树，或者是具有如下特性的二叉树：
1）若左子树不空，则左子树上所有结点的值均小于根结点的值；
2）若右子树不空，则右子树上所有结点的值均大于根结点的值；
3）左、右子树也分别为二叉排序树。
（2）中序遍历和二叉排序（搜索）树的关系
（3）插入和生成
1）按规矩插入，刻意维护
- 对一个无序序列可通过构造二叉排序树而变成一个有序序列。构造树的过程就是对无序序列进行排序的过程。
- 如果插入的节点均在叶子节点位置，则无需移动其他节点。相当于在有序序列上插入记录而无需移动其他记录。
2）提前安排好插入过程
3）完整案例图形演示
4）Java代码实现二叉排序(搜索)树的插入生成
/**
* @author: 何建光——hjg_5282
* @create: 2022-01-31 14:52
* PS ==> 二叉 排序/搜索 树
*/
public class BinarySortTreeDemo {
public static void main(String[] args) {
int[] arr = {45,24,53,12,28,90,90};
BinarySortTree binarySortTree = new BinarySortTree();
//循环的添加结点到二叉排序树
for(int i = 0; i< arr.length; i++) {
binarySortTree.add(new Node(arr[i]));
}
//中序遍历二叉排序树
System.out.println("中序遍历二叉排序树~");
binarySortTree.infixOrder(); // 1, 3, 5, 7, 9, 10, 12
}
}
class BinarySortTree{
private Node root;
public Node getRoot() {
return root;
}
//添加结点的方法
public void add(Node node) {
if(root == null) {
root = node;//如果root为空则直接让root指向node
} else {
root.add(node);
}
}
//中序遍历
public void infixOrder() {
if(root != null) {
root.infixOrder();
} else {
System.out.println("二叉排序树为空，不能遍历");
}
}
}
class Node{
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
//添加结点的方法
//递归的形式添加结点，注意需要满足二叉排序树的要求
public void add(Node node) {
if(node == null) {
return;
}
if (node.value == this.value){
return;
}
//判断传入的结点的值，和当前子树的根结点的值关系
if(node.value < this.value) {
//如果当前结点左子结点为null
if(this.left == null) {
this.left = node;
} else {
//递归的向左子树添加
this.left.add(node);
}
} else { //添加的结点的值大于 当前结点的值
if(this.right == null) {
this.right = node;
} else {
//递归的向右子树添加
this.right.add(node);
}
}
}
//中序遍历
public void infixOrder() {
if(this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if(this.right != null) {
this.right.infixOrder();
}
}
}
（4）二叉排序树的查找并删除
1）情况一：删除叶子节点
思路
(1)需求先去找到要删除的结点 targetNode
(2)找到 targetNode 的 父结点 parent
(3)确定 targetNode 是 parent 的左子结点 还是右子结点
(4)根据前面的情况来对应删除左子结点 parent.left = null
右子结点 parent.right = null;
2）情况二：被删除结点只有左子树或只有右子树
思路
- (1)需求先去找到要删除的结点 targetNode
- (2)找到 targetNode 的 父结点 parent
- (3)确定 targetNode 的子结点是左子结点还是右子结点
- (4)targetNode 是 parent 的左子结点还是右子结点
- (5)如果 targetNode 有左子结点
_5.1 如果 targetNode 是 parent 的左子结点
parent.left = targetNode.left;
_5.2 如果 targetNode 是 parent 的右子结点
parent.right = targetNode.left; - (6) 如果 targetNode 有右子结点
_6.1如果 targetNode 是 parent 的左子结点
parent.left = targetNode.right;
_6.2如果 targetNode 是 parent 的右子结点
parent.right = targetNode.right
3）情况三：被删除的结点既有左子树也有右子树
思路
(1)需求先去找到要删除的结点 targetNode
(2)找到 targetNode 的 父结点 parent
(3)从 targetNode 的右子树找到最小的结点
(4)用一个临时变量，将 最小结点的值保存 temp
(5)删除该最小结点
(6)targetNode.value = temp
4）查找目标节点及其对应的父节点代码
这里查找父节点的 searchParent 方法属实有点无奈之举，要是子节点中保存有父节点的信息就不用写这个方法了，
有了父节点和子节点，我们把子节点删除了，可以把剩下的嫁接到父节点上
//创建Node结点
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
//查找要删除的结点
/**
*
* @param value 希望删除的结点的值
* @return 如果找到返回该结点，否则返回null
*/
public Node search(int value) {
if(value == this.value) { //找到就是该结点
return this;
} else if(value < this.value) {//如果查找的值小于当前结点，向左子树递归查找
//如果左子结点为空
if(this.left == null) {
return null;
}
return this.left.search(value);
} else { //如果查找的值不小于当前结点，向右子树递归查找
if(this.right == null) {
return null;
}
return this.right.search(value);
}
}
//查找要删除结点的父结点
/**
*
* @param value 要找到的结点的值
* @return 返回的是要删除的结点的父结点，如果没有就返回null
*/
public Node searchParent(int value) {
//如果当前结点就是要删除的结点的父结点，就返回
if((this.left != null && this.left.value == value) ||
(this.right != null && this.right.value == value)) {
return this;
} else {
//如果查找的值小于当前结点的值, 并且当前结点的左子结点不为空
if(value < this.value && this.left != null) {
return this.left.searchParent(value); //向左子树递归查找
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value); //向右子树递归查找
} else {
return null; // 没有找到父结点
}
}
}
}
5）对应上面三种删除情况的代码（情况三-嫁接左子树最小）
//编写方法:
//1. 返回的 以node 为根结点的二叉排序树的最小结点的值
//2. 删除node 为根结点的二叉排序树的最小结点
/**
* @param node 传入的结点(当做二叉排序树的根结点)
* @return 返回的 以node 为根结点的二叉排序树的最小结点的值
*/
public int delRightTreeMin(Node node) {
Node target = node;
//循环的查找左子节点，就会找到最小值
while(target.left != null) {
target = target.left;
}
//这时 target就指向了最小结点
//删除最小结点
delNode(target.value);
return target.value;
}
//删除结点
public void delNode(int value) {
if(root == null) {
return;
}else {
//1.需求先去找到要删除的结点 targetNode
Node targetNode = search(value);
//如果没有找到要删除的结点
if(targetNode == null) {
return;
}
//如果我们发现当前这颗二叉排序树只有一个结点，根节点
if(root.left == null && root.right == null) {
root = null;
return;
}
//去找到targetNode的父结点
Node parent = searchParent(value);
//情况一：如果要删除的结点是叶子结点
if(targetNode.left == null && targetNode.right == null) {
//判断targetNode 是父结点的左子结点，还是右子结点
if(parent.left != null && parent.left.value == value) { //是左子结点
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {//是右子结点
parent.right = null;
}
//情况三：删除有两颗子树的节点
} else if (targetNode.left != null && targetNode.right != null) {
int minVal = delRightTreeMin(targetNode.right);
targetNode.value = minVal;
//情况二：删除只有一颗子树的结点
} else {
//如果要删除的结点只有 左子结点
if(targetNode.left != null) {
if(parent != null) {
//如果 targetNode 是 parent 的左子结点
if(parent.left.value == value) {
parent.left = targetNode.left;
} else { // targetNode 是 parent 的右子结点
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
//如果要删除的结点只有 右子结点
} else {
if(parent != null) {
//如果 targetNode 是 parent 的左子结点
if(parent.left.value == value) {
parent.left = targetNode.right;
} else { //如果 targetNode 是 parent 的右子结点
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
6）对应上面三种删除情况的代码（情况三-嫁接右子树最大）
修改两个地方
- 添加找子树最大的方法
//编写方法:
//1. 返回的 以node 为根结点的二叉排序树的最大结点的值
//2. 删除node 为根结点的二叉排序树的最大结点
/**
* @param node 传入的结点(当做二叉排序树的根结点)
* @return 返回的 以node 为根结点的二叉排序树的最大结点的值
*/
public int delLeftTreeMax(Node node) {
Node target = node;
//循环的查找左子节点，就会找到最小值
while(target.right != null) {
target = target.right;
}
//这时 target就指向了最小结点
//删除最小结点
delNode(target.value);
return target.value;
}
- 修改对应调用的方法
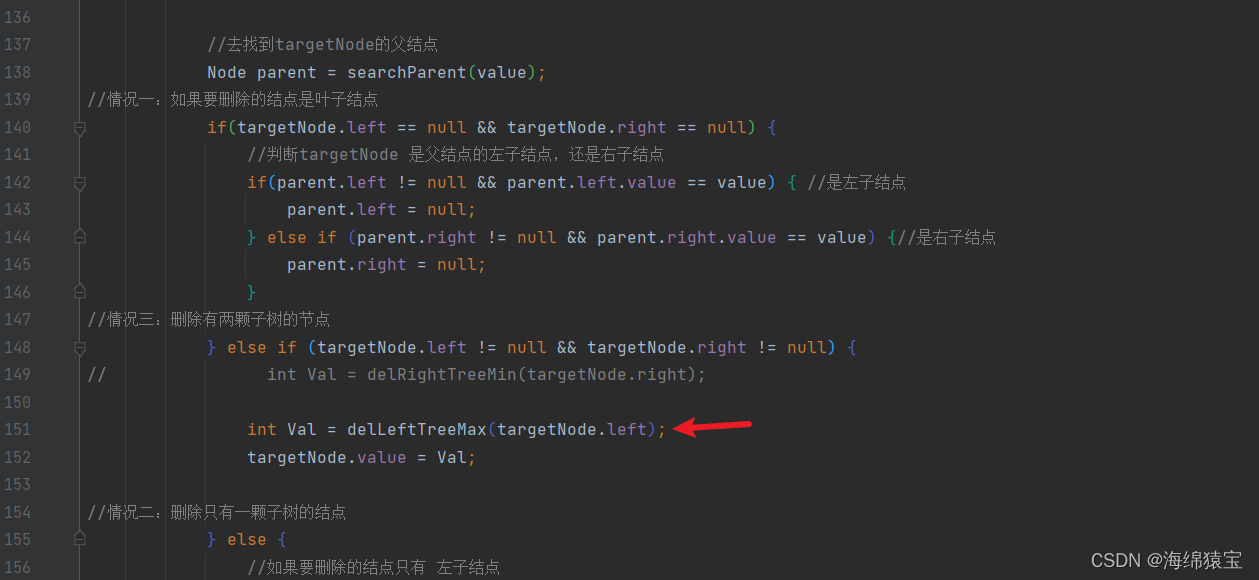
- 测试一下
再看一下示意图
（5）二叉排序树的查找过程分析
2、平衡二叉排序树
（1）解决的痛点
（2）定义
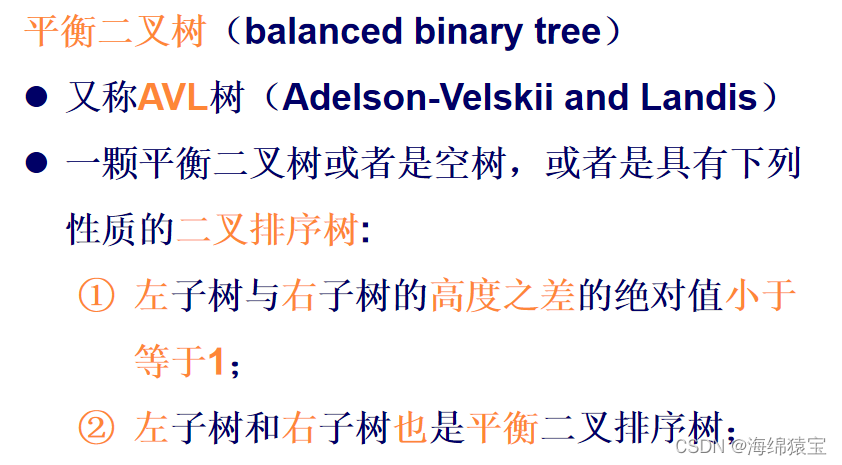
平衡二叉树的常用实现方法有红黑树、AVL、替罪羊树、Treap、伸展树等
（3）平衡二叉树平衡调整
（4）调整类型（4种也是2种: 左旋、右旋）
（5）案例图解演示
（6）左旋、右旋的Java代码
//左旋转方法
private void leftRotate() {
//创建新的结点，以当前根结点的值
Node newNode = new Node(value);
//把新的结点的左子树设置成当前结点的左子树
newNode.left = left;
//把新的结点的右子树设置成带你过去结点的右子树的左子树
newNode.right = right.left;
//把当前结点的值替换成右子结点的值
value = right.value;
//把当前结点的右子树设置成当前结点右子树的右子树
right = right.right;
//把当前结点的左子树(左子结点)设置成新的结点
left = newNode;
}
//右旋转
private void rightRotate() {
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
（7）完整代码，在插入时不断左右旋，保持平衡
代码
public class BinarySortTree_AVLTree {
public static void main(String[] args) {
//int[] arr = {4,3,6,5,7,8};
//int[] arr = { 10, 12, 8, 9, 7, 6 };
// int[] arr = { 10, 11, 7, 6, 8, 9 };
int[] arr = {16,3,7,11,9,26,18,14,15};
//创建一个 AVLTree对象
AVLTree avlTree = new AVLTree();
//添加结点
for(int i=0; i < arr.length; i++) {
avlTree.add(new Node(arr[i]));
}
//遍历
System.out.println("中序遍历");
avlTree.infixOrder();
System.out.println("在平衡处理~~");
System.out.println("树的高度=" + avlTree.getRoot().height()); //3
System.out.println("树的左子树高度=" + avlTree.getRoot().leftHeight()); // 2
System.out.println("树的右子树高度=" + avlTree.getRoot().rightHeight()); // 2
System.out.println("当前的根结点=" + avlTree.getRoot());//8
System.out.println("根节点的左子节点"+avlTree.getRoot().right);
System.out.println("根节点的右子节点"+avlTree.getRoot().left);
}
}
// 创建AVLTree
class AVLTree {
private Node root;
public Node getRoot() {
return root;
}
// 查找要删除的结点
public Node search(int value) {
if (root == null) {
return null;
} else {
return root.search(value);
}
}
// 查找父结点
public Node searchParent(int value) {
if (root == null) {
return null;
} else {
return root.searchParent(value);
}
}
// 编写方法:
// 1. 返回的 以node 为根结点的二叉排序树的最小结点的值
// 2. 删除node 为根结点的二叉排序树的最小结点
/**
*
* @param node
* 传入的结点(当做二叉排序树的根结点)
* @return 返回的 以node 为根结点的二叉排序树的最小结点的值
*/
public int delRightTreeMin(Node node) {
Node target = node;
// 循环的查找左子节点，就会找到最小值
while (target.left != null) {
target = target.left;
}
// 这时 target就指向了最小结点
// 删除最小结点
delNode(target.value);
return target.value;
}
// 删除结点
public void delNode(int value) {
if (root == null) {
return;
} else {
// 1.需求先去找到要删除的结点 targetNode
Node targetNode = search(value);
// 如果没有找到要删除的结点
if (targetNode == null) {
return;
}
// 如果我们发现当前这颗二叉排序树只有一个结点
if (root.left == null && root.right == null) {
root = null;
return;
}
// 去找到targetNode的父结点
Node parent = searchParent(value);
// 如果要删除的结点是叶子结点
if (targetNode.left == null && targetNode.right == null) {
// 判断targetNode 是父结点的左子结点，还是右子结点
if (parent.left != null && parent.left.value == value) { // 是左子结点
parent.left = null;
} else if (parent.right != null && parent.right.value == value) {// 是由子结点
parent.right = null;
}
} else if (targetNode.left != null && targetNode.right != null) { // 删除有两颗子树的节点
int minVal = delRightTreeMin(targetNode.right);
targetNode.value = minVal;
} else { // 删除只有一颗子树的结点
// 如果要删除的结点有左子结点
if (targetNode.left != null) {
if (parent != null) {
// 如果 targetNode 是 parent 的左子结点
if (parent.left.value == value) {
parent.left = targetNode.left;
} else { // targetNode 是 parent 的右子结点
parent.right = targetNode.left;
}
} else {
root = targetNode.left;
}
} else { // 如果要删除的结点有右子结点
if (parent != null) {
// 如果 targetNode 是 parent 的左子结点
if (parent.left.value == value) {
parent.left = targetNode.right;
} else { // 如果 targetNode 是 parent 的右子结点
parent.right = targetNode.right;
}
} else {
root = targetNode.right;
}
}
}
}
}
// 添加结点的方法
public void add(Node node) {
if (root == null) {
root = node;// 如果root为空则直接让root指向node
} else {
root.add(node);
}
}
// 中序遍历
public void infixOrder() {
if (root != null) {
root.infixOrder();
} else {
System.out.println("二叉排序树为空，不能遍历");
}
}
}
// 创建Node结点
class Node {
int value;
Node left;
Node right;
public Node(int value) {
this.value = value;
}
// 返回左子树的高度
public int leftHeight() {
if (left == null) {
return 0;
}
return left.height();
}
// 返回右子树的高度
public int rightHeight() {
if (right == null) {
return 0;
}
return right.height();
}
// 返回 以该结点为根结点的树的高度
public int height() {
return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}
//左旋转方法
private void leftRotate() {
//创建新的结点，以当前根结点的值
Node newNode = new Node(value);
//把新的结点的左子树设置成当前结点的左子树
newNode.left = left;
//把新的结点的右子树设置成带你过去结点的右子树的左子树
newNode.right = right.left;
//把当前结点的值替换成右子结点的值
value = right.value;
//把当前结点的右子树设置成当前结点右子树的右子树
right = right.right;
//把当前结点的左子树(左子结点)设置成新的结点
left = newNode;
}
//右旋转
private void rightRotate() {
Node newNode = new Node(value);
newNode.right = right;
newNode.left = left.right;
value = left.value;
left = left.left;
right = newNode;
}
// 查找要删除的结点
/**
*
* @param value
* 希望删除的结点的值
* @return 如果找到返回该结点，否则返回null
*/
public Node search(int value) {
if (value == this.value) { // 找到就是该结点
return this;
} else if (value < this.value) {// 如果查找的值小于当前结点，向左子树递归查找
// 如果左子结点为空
if (this.left == null) {
return null;
}
return this.left.search(value);
} else { // 如果查找的值不小于当前结点，向右子树递归查找
if (this.right == null) {
return null;
}
return this.right.search(value);
}
}
// 查找要删除结点的父结点
/**
*
* @param value
* 要找到的结点的值
* @return 返回的是要删除的结点的父结点，如果没有就返回null
*/
public Node searchParent(int value) {
// 如果当前结点就是要删除的结点的父结点，就返回
if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {
return this;
} else {
// 如果查找的值小于当前结点的值, 并且当前结点的左子结点不为空
if (value < this.value && this.left != null) {
return this.left.searchParent(value); // 向左子树递归查找
} else if (value >= this.value && this.right != null) {
return this.right.searchParent(value); // 向右子树递归查找
} else {
return null; // 没有找到父结点
}
}
}
@Override
public String toString() {
return "Node [value=" + value + "]";
}
// 添加结点的方法
// 递归的形式添加结点，注意需要满足二叉排序树的要求
public void add(Node node) {
if (node == null) {
return;
}
// 判断传入的结点的值，和当前子树的根结点的值关系
if (node.value < this.value) {
// 如果当前结点左子结点为null
if (this.left == null) {
this.left = node;
} else {
// 递归的向左子树添加
this.left.add(node);
}
} else { // 添加的结点的值大于 当前结点的值
if (this.right == null) {
this.right = node;
} else {
// 递归的向右子树添加
this.right.add(node);
}
}
//当添加完一个结点后，如果: (右子树的高度-左子树的高度) > 1 , 左旋转
if(rightHeight() - leftHeight() > 1) {
//如果它的右子树的左子树的高度大于它的右子树的右子树的高度
if(right != null && right.leftHeight() > right.rightHeight()) {
//先对右子结点进行右旋转
right.rightRotate();
//然后在对当前结点进行左旋转
leftRotate(); //左旋转..
} else {
//直接进行左旋转即可
leftRotate();
}
return ; //必须要!!!
}
//当添加完一个结点后，如果 (左子树的高度 - 右子树的高度) > 1, 右旋转
if(leftHeight() - rightHeight() > 1) {
//如果它的左子树的右子树高度大于它的左子树的高度
if(left != null && left.rightHeight() > left.leftHeight()) {
//先对当前结点的左结点(左子树)->左旋转
left.leftRotate();
//再对当前结点进行右旋转
rightRotate();
} else {
//直接进行右旋转即可
rightRotate();
}
}
}
// 中序遍历
public void infixOrder() {
if (this.left != null) {
this.left.infixOrder();
}
System.out.println(this);
if (this.right != null) {
this.right.infixOrder();
}
}
}
效果
扫一扫
480
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
