【机器学习基石】感知机模型+PLA（二）

最新推荐文章于 2021-11-07 16:52:31 发布

比奇堡咻飞兜

最新推荐文章于 2021-11-07 16:52:31 发布

阅读量775

点赞数 3

CC 4.0 BY-SA版权

分类专栏：机器学习文章标签：机器学习 PLA算法感知机模型

本文链接：https://blog.youkuaiyun.com/weixin_46308081/article/details/119453171

机器学习专栏收录该内容

17 篇文章

订阅专栏

本文深入探讨了感知机模型在信用评分场景的应用，通过权重和阈值确定是否发放信用卡。接着，介绍了 PLA（Perceptron Learning Algorithm）作为机器学习的第一个算法，详细阐述了其迭代过程和优化策略。对于线性可分数据，PLA 的收敛性得到了证明，展示了其在找到正确分类超平面的有限次迭代能力。此外，还提到了PacketAlgorithm作为处理非完美线性可分情况的策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

写在前面

本节内容主要介绍了感知机模型，还提出了机器学习中的第一个算法PLA，最后对PLA进行了优化得出Packet Algorithm。公式性的推导比较多。

本文整理自台湾大学林轩田的《机器学习基石》

1.感知机模型

$\bullet$ 引例：银行需要对客户进行判断是否可以给他们发放信用卡。现在收集客户资料，分别收集每个客户的年龄、年薪、工作年龄以及现在的负债。然后就这些因素下面我们使用感知机(Preceptron)模型进行进行分析。

$\bullet$ 建立模型

$\triangleright$ 个体 $x=(x_{1},x_{2},x_{3},...x_{d})$ ， $x_{i}$ 表示客户 $x$ 的属性，我们根据每个属性的重要程度分别为其设置一个权重 $w_{i}$ (weight)，那么对应属性与对应权重的乘积就可以表示我们对该客户的打分情况。

$\triangleright$ 同时设置一个阈值 $t h r e s h o l d$ ，如果打分大于阈值的话就发放信用卡，反之，则不发放信用卡。

$\begin{cases} & \text{ } {\textstyle \sum_{i=1}^{d}}w_{i}x_{i}>threshold & \text{ 放发信用卡 } \\ & \text{ } {\textstyle \sum_{i=1}^{d}}w_{i}x_{i}<threshold & \text{ 不放发信用卡 } \end{cases}$

$\triangleright$ 返回值 $y:\left \{ +1(good),-1(bad) \right \}$ ，我们可以设置+1（正数）发放，-1（负数）不发放。0的话情况比较少见，则忽略，随便进行选择。

可以建立一个函数来进行表示，标红的变量为函数影响因素：
${\color{red}h}(x)=sign((\sum_{i=1}^{d} {\color{red}w_{i}}x_{i})-{\color{red}threshold})$

$\triangleright$ 函数优化：因为现在 $h (x)$ 的表达式还比较凌乱，我们进行设置使其变得更整齐一点。我们设置：
$w_{0} = -threshold,\ x_{0}=+1$

那么就可以将该项合并到求和中，也就是( $w 、 x$ 为两个向量)：
${\color{red}h}(x) = sign(\sum_{i=0}^{d}w_{i}x_{i})=sign({\color{red}w^{T}}x)$ ( $w 、 x$ 为两个向量)

$\bullet$ 分析：

我们以两个维度为例进行分析，也就是 $x = (x_{1},x_{2})$

那么函数为：
$h(x) = sign(w_{0}+w_{1}x_{1}+w_{2}x_{2})$

其中 $x$ 就可以表示为二维平面内的点； $y$ 的话可以用点的形状来反映，我们设置 o 表示+1，× 表示-1；而假设 $h$ 就为二维平面内的直线（我们把它叫做 $\ classifiers$ ），直线一边表示发信用卡，一边表示不发信用卡；权重 $w$ 不同，对应的直线就不同，表示不同的假设情况。如下图所示：

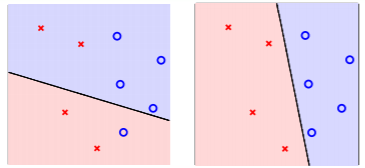
在这里插入图片描述
当图形中 o 在直线一边，× 在直线一边时，此时模型最优，准确率最高。

2.PLA算法

我们希望最终从假设集中寻找到的函数 $g$ 最接近理想函数 $f$ ，所以就需要介绍一下寻找最优函数的过程。

$\bullet$ PLA过程

$\triangleright$ 首先随机选择一条直线 $g_{0}$ ，下面我们用 $w_{0}$ （权重向量）来辅助进行观察， $w_{0}$ 相当与直线的法线（垂直于该直线）。当点判断出错时，就进行纠正，直到所有点都准确无误即可(这也被叫做循环PLA)。

$\triangleright$ 我们开始找犯错的点，一共有两种情况。第一种是点本来是正，结果判断为负。即现在 $w_{t}^{T}x_{n(t)}<0$ （t表示第t次纠正），那就表示 $w$ 与 $x$ 的夹角大于90°，也就是 $x$ 被误分在直线下侧，法向量方向为正方向，那么为了纠正的话就需要将角度缩小，也就是让 $w = w + y x, y = 1$ 。另一种是点本来为负，结果误分为正。即现在 $w_{t}^{T}x_{n(t)}>0$ ，那就表示 $w$ 与 $x$ 的夹角小于90°，也就是 $x$ 被误分在直线上侧，法向量方向为正方向，那么为了纠正的话就需要将角度扩大，也就是让 $w = w + y x, y = - 1$ 。

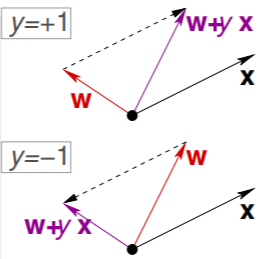
在这里插入图片描述
综上所述：调整公式就为 $w_{t+1} \gets w_{t} + y_{n(t)}x_{n(t)}$

$\bullet$ PLA算法可以停止的要求：首先前提就是存在直线将两个部分完全分割开，这种情况我们叫线性可分（linear separable）。如果是非线性可分的，那么PLA就不会停止。

$\bullet$ 练习

让 $n = n (t)$ ，通过下面的PLA规则，判断哪个公式是错误的。
$sign(w_{t}^{T}x_{n})≠y_{n},\ w_{t+1} \gets w_{t}+y_{n}x_{n}$

a. $w_{t+1}^{T}x_{n}=y_{n}$

b. $sign(w_{t}^{T}x_{n})=y_{n}$

c. $y_{n}w_{t+1}^{T}x_{n}≥y_{n}w_{t}^{T}x_{n}$

d. $y_{n}w_{t+1}^{T}x_{n}<y_{n}w_{t}^{T}x_{n}$

对于a，b来说，纠正后这个点是符合规律了，但是其他点还有可能出错，所以a，b错误。

对于c，d来说，我们在上面第二个式子左右两边同时乘以 $y_{n}x_{n}$ 就会发现左边恒加了一个非负数，所以选c。

3. PLA中的公式

对于线性可分的数据样本D，存在 $w_{f}$ 使得 $y_{n}=sign(w_{f}^{T}x_{n})$ ，使得正负两部分完全分开。

$\bullet$ 因为 $y_{n}$ 和 $w_{f}^{T}x_{n}$ 符号相同，所以它们的乘积（表示到直线的距离）恒大于0，所以存在：
$y_{n(t)}w_{f}^{T}x_{n(t)}≥\underset{n}{min} \ y_{n}w_{f}^{T}x_{n}>0$

PLA会对每次错误的点进行纠正，每次更新 $w_{t}$ 以后该直线也与目标直线更为接近，体现在 $w_{f}^{T}$ 与 $w_{t}$ 的内积更大，过程如下：
$w_{f}^{T}w_{t+1}=w_{f}^{T}(w_{t}+y_{n(t)}x_{n(t)})≥w_{f}^{T}w_{t}+\underset{n}{min} \ y_{n}w_{f}^{T}x_{n}＞w_{f}^{T}w_{t}+0$

但是内积变大并不一定是角度变小使得更接近目标直线，也有可能是向量长度变大了，下面我们验证 $w_{t+1}$ 和 $w_{t}$ 的长度关系：

$\left \| \underset{}{} w_{t+1} \right \|^{2} = \left \| \underset{}{} w_{t}+y_{n(t)}x_{n(t)} \right \|^{2}≤\left \| \underset{}{} w_{t} \right \|^{2}+0+\left \| \underset{}{} y_{n(t)}x_{n(t)} \right \|^{2}≤\left \| \underset{}{} w_{t} \right \|^{2}+\underset{n}{max} \ \left \| \underset{}{} y_{n}x_{n} \right \|^{2}$

很明显可以看出来向量长度是在缓慢的增长，所以确实是向量角度变小了，每次纠正过后更加接近目标函数了。

$\bullet$ 那么迭代 $T$ 次以后结果如何呢，我们接着上面的式子进行分析：

$w_{f}^{T}w_{t}≥w_{f}^{T}w_{t-1}+\underset{n}{min} \ y_{n}w_{f}^{T}x_{n}≥w_{0}+T\underset{n}{min} \ y_{n}w_{f}^{T}x_{n}（T次迭代以后）≥T\underset{n}{min} \ y_{n}w_{f}^{T}x_{n}$

该向量的长度变为：
$\left \| \underset{}{} w_{t} \right \|^{2}≤\left \| \underset{}{} w_{t-1} \right \|^{2}+\underset{n}{max} \ \left \| \underset{}{} x_{n} \right \|^{2}≤\left \| \underset{}{} w_{0} \right \|+T\underset{n}{max} \ \left \| \underset{}{} x_{n} \right \|^{2}（T次迭代以后）=T\underset{n}{max} \ \left \| \underset{}{} x_{n} \right \|^{2}$

所以根据上面两个式子最终可以得出：
$\frac{w_{f}^{T}}{\left \| \underset{}{} w_{f}\right \| } \frac{w_{T}}{\left \| \underset{}{}w_{T} \right \| }=\frac{T\underset{n}{min} \ y_{n}w_{f}^{T}x_{n}}{\left \| \underset{}{} w_{f}^{T} \right \| *\left \| \underset{}{} w_{t}\right \| }≥\frac{T\underset{n}{min} \ y_{n}w_{f}^{T}x_{n}}{\left \| \underset{}{} w_{f}^{T} \right \| * \sqrt T*\underset{n}{max} \ \left \| \underset{}{} x_{n} \right \|}=\sqrt T *constant$

因为上式左半部分实际上计算的是 $w_{T}$ 与 $w_{f}$ 之间夹角的余弦值，所以我们可以知道该式一定小于等于1，在这里我们重新定义两个变量用来简化上式，分别为：
$R^{2} =\underset{n}{max} \ \left \| \underset{}{} x_{n} \right \|^{2} , ρ = \underset{n}{min} \ y_{n} \frac{w_{f}^{T}}{ \left \| \underset{}{} w_{f} \right \|}x_{n}$

所有可以得到：
$\frac{T\underset{n}{min} \ y_{n}w_{f}^{T}x_{n}}{\left \| \underset{}{} w_{f}^{T} \right \| * \sqrt T*\underset{n}{max} \ \left \| \underset{}{} x_{n} \right \|}≤1\Leftrightarrow T ≤\frac{R^{2}}{ρ^{2}}$

此时同样可以发现迭代次数 $T$ 存在上限，所以对于线性可分的情况迭代次数一定是有限的。

4.其它关于PLA的内容

$\bullet$ 虽然上面证明了对于线性可分情况下迭代次数是有限的，但是实际情况下我们并不知道是否为线性可分，其次就算我们知道是线性可分，但是迭代次数是多少同时还是未知的。

$\bullet$ 所以我们可以适当容忍一些点的错误，在这里使用类似贪心策略的方法寻找函数 $g$ ，该方法被叫做 Packet Algorithm。首先我们还是需要初始化一条直线，记录错误的点数，然后更新权重 $w$ ，得到新的直线再记录错误点数，选取并存储错误点数较少的权重向量 $w$ ，之后重复该操作到一定次数以后，记录的权重就是最优权重。