【深度学习基础】

实现最简单的全连接层（线性层）

//直接调用pytorch里包含的函数

import torch.nn as nn
linear_layer = nn.Linear(in_features, out_features, bias=True)

//用代码实现

class Linear:
    def __init__(self, in_features, out_features,bias=True):
        self.weight =  torch.randn(out_features, in_features,requires_grad=True)
        if bias:
            self.bias = torch.randn(out_features, requires_grad=True)
        else:
            self.bias = None
    def __call__(self, x):
        self.out = x @ self.weight
        if self.bias is not None:
            self.out += self.bias
        return self.out
    def parameters(self):
        if self.bias is not None:
            return [self.weight, self.bias]
        return [self.weight]

实现最简单的Sequential

它位于 torch.nn 模块中。torch.nn.Sequential 是一个容器
用于将多个神经网络层按顺序堆叠在一起，方便快速构建简单的神经网络模型。

// pytorch中的实现
import torch
import torch.nn as nn

# 定义一个简单的顺序模型
model = nn.Sequential(
    nn.Linear(2, 10),  # 输入特征维度为 2，输出特征维度为 10
    nn.ReLU(),         # ReLU 激活函数
    nn.Linear(10, 1)   # 输出层，输出特征维度为 1
)

# 打印模型结构
print(model)

// 自己定义
class Sequential:
    def __init__(self, layers):
        self.layers = layers
    def __call__(self, x):
        for l in self.layers:
            x = l(x)
        self.out = x
        return self.out
    def parameters(self):
        params_list = []  # 创建一个空列表，用于存储所有层的参数
        for layer in self.layers:  # 遍历每一层
            for p in layer.parameters():  # 遍历当前层的所有参数
                params_list.append(p)  # 将参数添加到列表中
        return params_list  # 返回包含所有参数的列表
    def predict_proba(self, x):
        if isinstance(x, np.ndarray):
            x = torch.tensor(x).float()
            logits = self(x) #将输入张量 x 传递给模型，计算模型的输出（logits，即未经激活函数处理的原始输出）
            #对 logits 应用 Softmax 函数，将其转换为概率分布
            self.prob = torch.nn.functional.softmax(logits, dim=-1).detach().numpy()
            return self.prob

实现最简单的sigmoit激活函数

//经过全连接层输出的Logits需要经过激活函数才能变成非线性的数据
常见的激活函数有sigmoit和Softmax，这两个激活函数的输出都是概率值
区别在于sigmoit函数常用于二分类任务
softmax函数常用于多分类任务，这里各个不同分类的概率加总是1

class Sigmoid:
    def __call__(self, x):
        self.out = torch.sigmoid(x)
        return self.out
    def parameters(self):
        return []

实现最简单的优化器

// 常见的优化器有SGD（随机梯度下降），Adam（自适应矩估计）等

optimizer = torch.optim.SGD(model.parameters(), lr=0.1)
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

    with torch.no_grad():
        for p in model.parameters():
            p -= learning_rate * p.grad
            p.grad = None

残差网络

残差连接的作用

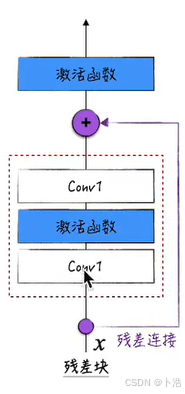
1、缓解梯度消失问题：
在深度网络中，梯度反向传播时可能会逐渐变小，导致靠近输入层的参数难以更新。
残差连接提供了一条“捷径”，使梯度能够直接回传到浅层，缓解了梯度消失问题。
2、解决网络退化问题：
随着网络深度增加，传统网络的性能可能会饱和甚至下降，这种现象称为网络退化。
残差连接允许网络学习恒等映射（Identity Mapping）即 F(x)=0，从而避免性能退化。
3、简化优化：
学习残差映射 F(x)=H(x)−x 比直接学习目标映射 H(x)更容易，因为 F(x)通常是一个较小的增量。

然而想要在激活函数前进行加值，则需要在经历卷积层后不改变输入张量的形状
第一种方法：保证卷积层输入输出张量一样
张量形状计算公式为（输入长宽-卷积核大小+2填充大小）/步长+1*

// 例如这样的卷积层就不会改变张量形状
channels = torch.randit(1,10,(1,))
conv1 = nn.Conv2d(channels,channels,(3,3),stride=1,padding=1)

残差块代码实现

// An highlighted block
class ResidualBlockSimplified(nn.Module):
    def __init__(self,channels):
        super().__init__()
        self.conv1 = nn.Conv2d(channels, channels, (3, 3), stride=1, padding=1)
        self.conv2 = nn.Conv2d(channels, channels, (3, 3), stride=1, padding=1)
    def forward(self, x):
        inputs = x
        x = F.relu(self.conv1(x))
        x = self.conv2(x)
        #残差链接
        out = x + inputs
        out = F.relu(out)
        return out

第二种方法：加值的部分也经过一个卷积层以达到可以和输入张量形状一样的目的

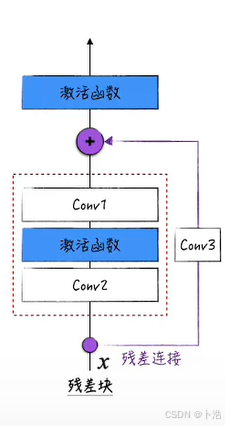
// 把x改造成经过两层卷积层输出后的形状
 if stride != 1 or in_channels != out_channels:
            self.downsample = nn.Conv2d(in_channels, out_channels,(1,1), stride=stride,padding=0)

残差块代码实现

// An highlighted block
class ResidualBlock(nn.Module):
    def __init__(self,in_channels,out_channels,stride=1):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels, out_channels, (3, 3), stride=stride, padding=1)
        #归一化层，后面会提
        self.bn1 = nn.BatchNorm2d(out_channels)
        self.conv2 = nn.Conv2d(out_channels, out_channels, (3, 3), stride=1, padding=1)
        #归一化层，后面会提
        self.bn2 = nn.BatchNorm2d(out_channels)
        self.downsample = None
        if stride != 1 or in_channels != out_channels:
            self.downsample = nn.Conv2d(in_channels, out_channels,(1,1), stride=stride,padding=0)
            #归一化层，后面会提
            self.bn3 = nn.BatchNorm2d(out_channels)

    def forward(self, x):
        inputs = x
        x = F.relu(self.conv1(x))
        x = self.conv2(x)
        if self.downsample is not None:
            inputs = self.downsample(inputs)
        out = x + inputs
        out = F.relu(out)
        return out

残差连接通常用在比较深的神经网络里，这一般需要与其他的优化手段配合在一起使用，比如说批归一化层
在pythorch中直接提供了多维批量归一化的函数BatchNorm2d。

// An highlighted block
import torch
import torch.nn as nn

# 创建一个 BatchNorm2d 实例
# 假设你的卷积层输出有 32 个通道
bn = nn.BatchNorm2d(num_features=32)

# 创建一个随机的卷积层输出数据
# 假设 batch_size=4, height=28, width=28
conv_output = torch.randn(4, 32, 28, 28)

# 使用 BatchNorm2d 对数据进行归一化
normalized_output = bn(conv_output)

print(normalized_output.shape)  # 输出形状仍然是 [4, 32, 28, 28]

残差网络结构

残差网络代码实现

// 叠加残差块
class ResNet(nn.Module):
    
    def __init__(self):
        super().__init__()
        self.block1 = ResidualBlock(1, 20)
        self.block2 = ResidualBlock(20, 40, stride=2)
        self.block3 = ResidualBlock(40, 60, stride=2)
        self.block4 = ResidualBlock(60, 80, stride=2)
        self.block5 = ResidualBlock(80, 100, stride=2)
        self.block6 = ResidualBlock(100, 120, stride=2)
        self.fc = nn.Linear(120, 10)
        
    def forward(self, x):
        # x : (B, 1, 28, 28)
        B = x.shape[0]
        x = self.block1(x)  # (B, 20, 28, 28)
        x = self.block2(x)  # (B, 40, 14, 14)
        x = self.block3(x)  # (B, 60,  7,  7)
        x = self.block4(x)  # (B, 80,  4,  4)
        x = self.block5(x)  # (B, 100, 2,  2)
        x = self.block6(x)  # (B, 120, 1,  1)
        x = self.fc(x.view(B, -1))
        return x