Self-supervised Knowledge Distillation using Singular Value Decomposition（2018ECCV）----阅读笔记

最新推荐文章于 2022-04-19 21:50:50 发布

原创最新推荐文章于 2022-04-19 21:50:50 发布

· 902 阅读

9 ·

版权

文章标签：

#自然语言处理 #python #机器学习

知识蒸馏专栏收录该内容

14 篇文章

订阅专栏

Self-supervised Knowledge Distillation using Singular Value Decomposition----阅读笔记

创新点，最重要一点。
Abstract
Introduction
2 Related Works
3 Method
4 Experimental Results
代码贴出来好理解

创新点，最重要一点。

SVD 提取特征映射的知识，RBF计算两个特征映射的相关性。

Abstract

提出了一种新的基于奇异值分解（SVD）的知识提取方法。
将知识转移定义为一项自我监督的任务，并提出了一种持续接收T-DNN信息的方法。

Introduction

现有的T-S知识提取方法存在以下局限性：
（1）它们尚未从T-DNN中提取和提取丰富的信息。
（2）此外，T-S-DNN的结构非常有限。
（3）最后，由于从T-DNN中学习的知识仅用于初始化S-DNN的参数，因此随着下一个主要任务的学习进行，它将逐渐消失。
为了解决这一问题，本文从两个方面进行了探讨。第一种是适当地处理知识，以减少内存和计算量。因此，我们利用奇异值分解（SVD）对知识数据进行了优雅的压缩，SVD主要用于信号处理领域的特征降维[11,12,13]。我们还通过径向基函数（RBF）[14,15]分析了压缩特征映射之间的相关性，径向基函数通常用于核化学习。结果表明，与传统的T-DNN方法相比，SVD和RBF知识提取方法能够更有效地提取T-DNN的信息，并且无论特征图的空间分辨率如何，都可以进行知识的传递。第二，通过自我监督学习机制[16,17,18]，该机制学习自己创建标签，确保转移的知识不会消失并持续使用。也就是说，它可以解决T-DNN知识的消失问题。此外，自监督学习可以提供额外的性能改进，因为它允许更强大的正则化[8]。

2 Related Works

2.1 Knowledge Distillation

Yim等人[10]将从T-DNN传输到S-DNN的知识定义为特征图的变化，而不是图层参数的变化。他们确定了网络中的某个图层组，并将图层组的输入和输出特征映射之间的相关性定义为Gram矩阵，以便S-DNN和T-DNN的特征相关性变得相似。然而，上述技术定义的知识仍然缺乏信息，通过初始化进行的知识转移仍然有限。

Yim[10] A gift from knowledge distillation: Fast optimization, network minimization and transfer learning. In: The IEEE Conference
on Computer Vision and Pattern Recognition (CVPR). (2017)

上述技术定义的知识仍然缺乏信息，通过初始化进行的知识转移仍然有限。什么意思呢？缺乏什么信息？

2.2 SVD and RBF

RBF了解
RBF : 1985年，Powell提出了多变量插值的径向基函数（RBF）方法。径向基函数是一个取值仅仅依赖于离原点距离的实值函数，也就是Φ（x）=Φ(‖x‖),或者还可以是到任意一点c的距离，c点称为中心点，也就是Φ（x，c）=Φ(‖x-c‖)。任意一个满足Φ（x）=Φ(‖x‖)特性的函数Φ都叫做径向基函数，标准的一般使用欧氏距离（也叫做欧式径向基函数），尽管其他距离函数也是可以的。最常用的径向基函数是高斯核函数 ,形式为 k(||x-xc||)=exp{- ||x-xc||^2/(2*σ)2) } 其中x_c为核函数中心,σ为函数的宽度参数 , 控制了函数的径向作用范围。

SVD主要用于降维或从特征图中提取重要信息[11,12,13]。在[11]中，Alter等人表明，使用SVD可以提取数据集的信息。Lonescu等人根据SVD的链规则定义了梯度，并证明即使在使用SVD的DNN中，端到端学习也是可以实现的[13]。他们还表明，在特征图中汇集高级信息在识别和分割等特征分析任务中是非常有效的。径向基函数（RBF）是一个函数，它从距离中心的角度重新映射每个特征，使特征具有高维。RBF可用于各种核化学习或RBF网络（RBFN）[14,15]。特别是，使用径向基函数（如高斯函数）分析特征，可以更稳健地分析噪声数据。如果这两种方法能够很好地结合起来，就有可能从模糊和噪声数据中有效地提取重要信息。所提出的知识提取方法利用奇异值分解（SVD）从给定的特征映射中有效地提取核心知识，并利用RBF网络有效地计算两个特征映射之间的相关性。

SVD 提取特征映射的知识，RBF计算两个特征映射的相关性。

2.3 Training Mechanism

自监督学习生成标签并自行学习。最近，人们研究了各种自监督学习任务[16,17,18]，因为它们可以有效地初始化网络模型。在[18]中，提出了一种通过将各种自监督任务捆绑到多任务中一次学习各种自监督任务的方法，并证明该方法比传统方法更有效。另一方面，半监督学习是另一种在标记数据不足时同时使用标记和未标记数据的学习方案。为了解决缺乏训练目的数据集这一根本问题，人们积极开展了各种半监督学习研究[20,21]。我们将介绍上述自监督学习作为一种比现有T-S-DNN中通过知识转移进行参数初始化更有效的转移方法。

在这里插入图片描述

3 Method

DNN中指定两个特定的层点，并感测相应的两个特征映射。两点之间的图层定义为图层模块。
在层模块输入端感测的特征映射称为前端特征映射图（FFM），在输出端感测的特征映射称为后端特征映射图（BFM）。
例如，在MobileNet中，层模块可以由几个深度方向可分离的卷积组成。让FFM和BFM的深度分别为D_F和D_B。在本文中，每个DNN中的最大层模块数为G。现在我们可以通过蒸馏模块得到某一层模块的FFM和BFM之间的相关性。蒸馏模块从FFM和BFM的两个输入输出大小为k×D_F×D_B的蒸馏特征向量distillation feature vector（DFV）。见第二节。3.1.最后，我们提出了一种新的训练机制，使得来自T-DNN的知识不会在第二阶段即第二阶段消失。E主要任务学习过程。我们改进了[8]中介绍的自我监督学习，以实现更有效的知识转移。见第二节。3.2.

k×D_F×D_B 举例子 Mobilenet backbone层的某一层的输出特征图是 128 x 20 x 20 , 经过 FPN层某一层的输出特征图是 64 x 20 x 20
这两张特征图就是来说，称为 FPN层这某一层模块的 FFM , BFM ，他们的关系看 k x 128 x64 称为 DFV。

简单来说FFM，BFM分别为层模块的输入输出特征图（即一层网络模块的输入和输出特征图，比如backbone的输入和输出图）

3.1 Proposed Distillation Module

在这里插入图片描述
[10]的思想，利用特征图之间的相关性提取知识。然而，通过多个卷积层生成的特征图通常太大而无法使用，因为它们不仅计算成本高，而且很难学习。解决此问题的直观方法是减少特征图的空间维度。我们引入奇异值分解（SVD）来有效地去除特征映射中的空间冗余，并在降低特征维数的过程中获得有意义的隐含特征信息。本节详细描述了如何生成DFV，即（利用SVD蒸馏知识）。图2显示了所提出的知识提取模块的结构。假设T-DNN中定义的图层模块的输入和输出特征映射FFM和BFM是该蒸馏模块的输入。首先，利用截断奇异值分解消除特征映射的空间冗余。然后，对截断奇异值分解得到的右奇异向量V和奇异值矩阵进行后处理，以便于学习，得到k个特征向量。最后，通过径向基函数计算FFM和BFM得到的特征向量之间的相关性，得到秩为k的DFV（蒸馏特征向量）

Yim[10] A gift from knowledge distillation: Fast optimization, network minimization and transfer learning. In: The IEEE Conference
on Computer Vision and Pattern Recognition (CVPR). (2017)

这里具体什么意思，看一遍 [10]的代码就知道了
且我在这里改进了该代码，不用减少特征图的spitial dimension。
SVD 的本质还是降维，我们静静看后续。

Truncated SVD （截断奇异值分解）

目的是为了什么？
截断奇异值分解是知识提取模块的关键元素，因为它有效地降低了特征映射的维数。
什么是 Truncated SVD ？
回顾下先验知识
具体做法就是，预先确定矩阵 Σ 的秩，要得到 V 和 Σ ，为了最小化压缩，使得他们维度分别为 KxD 和 Kx1

在这里插入图片描述

在这里插入图片描述
论文这一段了解下，只不过对梯度M做一下解释，证明方法的可行性。
Hadmard product 对应元素相乘

Post-processing

在这里插入图片描述

具体做法：

第一步：F_T 归一化 F_T 作为压缩特征图特征信息（V 和 Σ ）后归一化

在这里插入图片描述

第二步：对齐
我们根据教师奇异值对齐学生奇异向量。因此，与教师奇异向量信息最相似的学生奇异向量按相同顺序对齐。这里，将奇异向量之间的相似度定义为余弦相似度的绝对值，余弦相似度通过两个向量之间的角度确定相似度，从而可以准确地测量方向相反的向量之间的相似度。

在这里插入图片描述

第三步：F_S 归一化

在这里插入图片描述

第二步第三步一起看，什么意思呢？
如何求 F_S ，求 f_S,i，怎么做呢？

首先是按老师的顺序 F_T 依次求的，用老师的归一化的奇异值约束， v_Align，i 则是求得和此时老师的奇异值的右奇异向量最相似的学生右奇异向量v （cosine 表向量相似性）

Computing Correlation using Radial Basis Function

通过对FFM和BFM应用所提出的SVD和后处理获得的特征向量基本上是彼此独立的离散随机向量。因此，我们将从FFM和BFM获得的特征向量集之间的相关性定义为如式（10）所示的逐点L2距离，并通过将高斯RBF应用于如式（9）所示的计算相关性来完成秩k DFV，以进行维扩展。
在这里插入图片描述 > 什么意思呢？
一句话简单来说，他也是求相关性，只不过是求的是，特征集 F 各个 f 的相关性

3.2 Training Mechanism

在这里插入图片描述
G为拟定T-S-DNN中定义的最大层模块数量。在这种情况下，假设所有层模块具有同等的重要性。

Total_loss

在这里插入图片描述
如果蒸馏损失远远大于主任务损失，则知识转移的梯度将变得过大，并且上述多任务学习可能无法正常工作。为了解决这个问题，有必要限制蒸馏任务的效果。因此，我们引入了梯度剪裁[22]来限制知识转移的梯度。

一般来说，裁剪的阈值是恒定的，但我们定义了主任务和转移任务的L2范数比率，如公式（13）所示，并使用该阈值自适应裁剪知识转移的梯度。
在这里插入图片描述
下面就是梯度裁剪

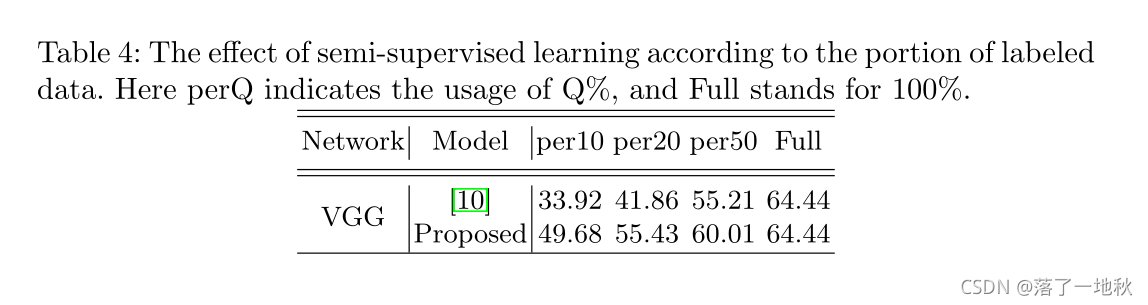
4 Experimental Results

这一部分看看论文。
在这里插入图片描述

在这里插入图片描述

代码贴出来好理解

from __future__ import print_function

import torch
import torch.nn as nn
import torch.nn.functional as F


class KDSVD(nn.Module):
    """
    Self-supervised Knowledge Distillation using Singular Value Decomposition
    original Tensorflow code: https://github.com/sseung0703/SSKD_SVD
    blog note: https://blog.youkuaiyun.com/weixin_46239293/article/details/120239048
    """

    def __init__(self, k=1):
        super(KDSVD, self).__init__()
        self.k = k  # 预设定的秩

    def forward(self, g_s, g_t):
        # g_s , g_t 分别为 某层模块的 FFM 和 BFM front-feature-map back-feature-map
        # 举例子 backbone一个尺度的输出 和 fpn一个尺度的输出 # g_s g_t [2,1,3,20,20] batch_size
        v_sb = None
        v_tb = None
        losses = []
        for i, f_s, f_t in zip(range(len(g_s)), g_s, g_t):
            # g_s g_t [2,1,3,20,20]
            # f_s , f_t [1,3,20,20]
            # 求出fs ft 的SVD且做了归一化
            u_t, s_t, v_t = self.svd(f_t, self.k)
            # print(u_t.shape,s_t.shape,v_t.shape) # torch.Size([1, 400, 1]) torch.Size([1, 1]) torch.Size([1, 3, 1])
            u_s, s_s, v_s = self.svd(f_s, self.k + 3)
            # print(u_s.shape, s_s.shape, v_s.shape) # torch.Size([1, 400, 3]) torch.Size([1, 3]) torch.Size([1, 3, 3])

            # 对齐
            v_s, v_t = self.align_rsv(v_s, v_t)
            # print(v_s.shape,v_t.shape) # torch.Size([1, 3, 1]) torch.Size([1, 3, 1])
            s_t = s_t.unsqueeze(1)  # 老师的奇异值
            v_t = v_t * s_t
            v_s = v_s * s_t

            # 得到最后的fs ft

            if i > 0:
                # 下面就是由RBF Radial Basis Function 径向基函数 求特征集 F 各个 f 的相关性,
                s_rbf = torch.exp(-(v_s.unsqueeze(2) - v_sb.unsqueeze(1)).pow(2) / 8)
                t_rbf = torch.exp(-(v_t.unsqueeze(2) - v_tb.unsqueeze(1)).pow(2) / 8)

                # 相关性的loss
                l2loss = (s_rbf - t_rbf.detach()).pow(2)
                l2loss = torch.where(torch.isfinite(l2loss), l2loss, torch.zeros_like(l2loss))
                losses.append(l2loss.sum())

            v_tb = v_t
            v_sb = v_s

        bsz = g_s[0].shape[0]
        losses = [l / bsz for l in losses]
        return losses

    def svd(self, feat, n=1):
        size = feat.shape
        # print(len(size)) # [1,3,20,20] N  C(D)  H  W 论文用 D 表示channel C
        assert len(size) == 4

        x = feat.view(-1, size[1], size[2] * size[2]).transpose(-2, -1)  # [1,400,3] N HW C(D)
        u, s, v = torch.svd(x)
        '''Computes the singular value decomposition of either a matrix or batch of matrices input. 
        The singular value decomposition is represented as a namedtuple (U, S, V), such that input = U diag(S) Vᴴ. 
        where Vᴴ is the transpose of V for real inputs, and the conjugate transpose of V for complex inputs. 
        If input is a batch of matrices, then U, S, and V are also batched with the same batch dimensions as input.'''
        u = self.removenan(u)
        s = self.removenan(s)
        v = self.removenan(v)

        if n > 0:
            u = F.normalize(u[:, :, :n], dim=1)
            s = F.normalize(s[:, :n], dim=1)
            v = F.normalize(v[:, :, :n], dim=1)

        return u, s, v

    @staticmethod
    def removenan(x):
        x = torch.where(torch.isfinite(x), x, torch.zeros_like(x))
        return x

    @staticmethod
    def align_rsv(a, b):
        # a v_s [1,3,3] b v_t [1,3,1]
        # a.transpose(-2, -1) 调换了 H W 转置
        cosine = torch.matmul(a.transpose(-2, -1), b)  # 矩阵相乘 [1,3,1]
        max_abs_cosine, _ = torch.max(torch.abs(cosine), 1, keepdim=True)  # 取相似度高的向量 [1,1,1]
        mask = torch.where(torch.eq(max_abs_cosine, torch.abs(cosine)),
                           torch.sign(cosine), torch.zeros_like(cosine))
        a = torch.matmul(a, mask)
        return a, b


import torch
import numpy as np

g_t = np.arange(0, 2400)
# print(a)
g_t = torch.from_numpy(g_t).view(2, 1, 3, 20, 20).float()
# print(a)
g_s = torch.ones([2, 1, 3, 20, 20]).float()

kdsvd = KDSVD()
loss = kdsvd.forward(g_t, g_s)