【数据结构与算法】二叉树基础与遍历的C语言实现
参考博文:
1. 程序内功篇六–树
2. 二叉树知识点最详细最全讲解
3. 二叉查找树(一)之 图文解析 和 C语言的实现
树的介绍
树的定义
树是n(n≥0)个节点的有限集合T,它满足两个条件 :
- 有且仅有一个特定的称为根(Root)的节点;
- 其余的节点可以分为m(m≥0)个互不相交的有限集合T1、T2、……、Tm,其中每一个集合又是一棵树,并称为其根的子树
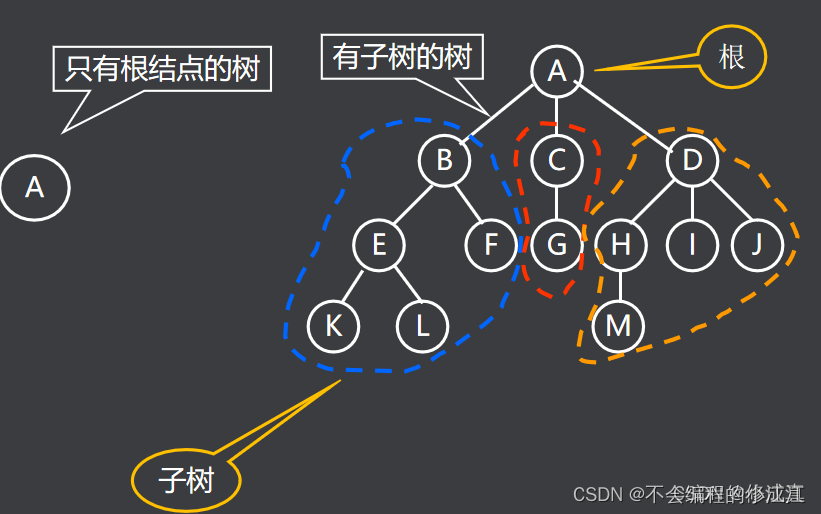
树的性质
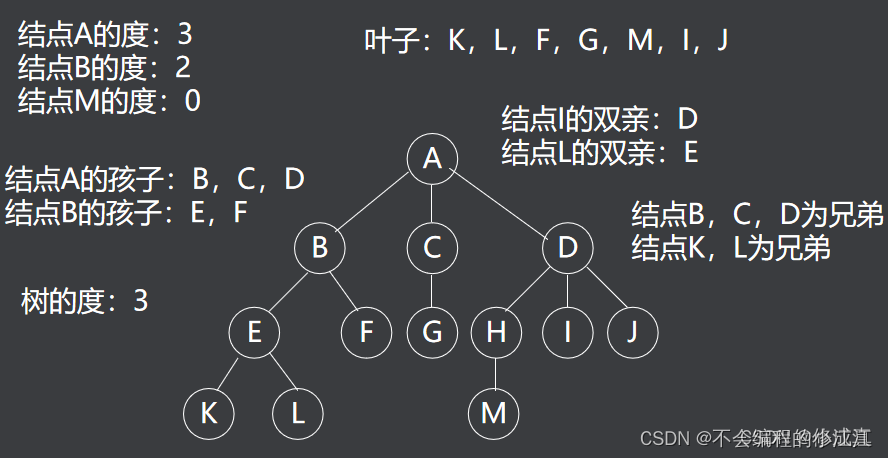
- 一个节点的子树的个数称为该节点的度数
- 一棵树的度数是指该树中节点的最大度数
- 度数为零的节点称为树叶或终端节点
- 度数不为零的节点称为分支节点
二叉树的介绍
提前感受一下现实中的二叉树长什么样

二叉树的定义
每个节点最多有两个子树的树结构

二叉树的性质
-
二叉树第i(i≥1)层上的节点数目最多为
2^(i-1)个 -
深度为k(k>=1)的二叉树至多有
2^k-1个节点 -
包含n个节点的二叉树的高度至少为log2 (n+1)。
二叉树的种类
(1)满二叉树
高度为h,并且由2^h–1个结点的二叉树,被称为满二叉树

(2) 完全二叉树
一颗二叉树中,只有最下面两层节点的度可以小于2,并且最下层的叶节点集中在靠左的若干位置上

完全二叉树特点: 叶子节点只能出现在最下层和次下层,且最下层的叶子节点集中在树的左部。显然,一颗满二叉树必定是一颗完全二叉树,而完全而二叉树不一定是满二叉树。
二叉树的存储方式
(1) 顺序存储
有n个节点的完全二叉树可以用有n+1个元素的数组进行顺序存储,节点号和数组下标一一对应,下标为零的元素不用。不完全二叉树通过添加虚节点构成完全二叉树,然后用数组存储,但这要浪费一些存储空间。

(2)链式存储
若对于一棵只有左子树或者右子树的树而言,若采用顺序存储的方式,需要添加大量的虚节点,在存储的空间上将浪费大量的地址空间,因此通常将二叉树以链式的结构进行存储,其中每个节点分为三个部分:
- 数据
- 左子树
- 右子树
示意图:

进一步抽象为程序结构体示意图:

程序结构体定义:
typedef char data_t; //节点数据类型
typedef struct node{
data_t data; //节点数据
struct node *left; //左子树
struct node *right; //右子树
}Bitree;
二叉树三种遍历方式
- 先序遍历: 先访问根节点,再访问左子树,最后访问右子树;(中左右)
- 中序序列: 先访问左子树,再访问根节点,最后访问右子树;(左中右)
- 后序序列: 先访问左子树,再访问右子树,最后访问根节点;(左右根)

遍历的实现(递归实现)
递归算法三要素
- 确定递归函数的参数和返回值:确定需要在递归过程中需要涉及与处理的参数,并明确每次递归的返回值是什么类型。
- 确定终止条件:即停止递归条件,如果递归没有终止,操作系统的内存栈必然就会溢出。
- 确定单层递归的逻辑:确定每一层递归需要处理的信息,在这里也就会重复调用自己来实现递归的过程。
补充一下: 递归算法的中间变量是存放在栈空间的,所以返回的时候是返回到上一级。
以前序遍历为例:
-
【确定递归函数的参数与返回值】
因为要打印出遍历节点的数值,所以参数里需要传入节点地址,除了这一点就不需要再处理什么数据了也不需要有返回值,所以递归函数返回类型就是void,代码如下:void preorder(Bitree* root) -
【确定终止条件】
在递归的过程中,如何算是递归结束了呢,当然是当前遍历的节点是空了,那么本层递归就要要结束了,所以如果当前遍历的这个节点是空,就直接return,代码如下:if(root == NULL) return ; -
【确定单层递归逻辑】
前序遍历是根左右的循序,所以在单层递归的逻辑,是要先取根节点的数值,然后再遍历左右子树,代码如下:printf("%c",root->data); //获取根节点数据 preorder(root->left); //继续遍历左子树 preorder(root->right); //继续遍历右子树
树的创建C程序设计(递归)
前面都在描述树的相关理论知识和遍历的内容,但程序遍历的实现是基于一棵现有的树而言的,因此这里通过先序遍历的方式创建一棵树,对于虚节点的地方通过输入 # 表示
Bitree* creat_bitree()
{
data_t ch;
Bitree* root;
scanf("%c",&ch); //输入节点数据
//空树
if(ch == '#')
return NULL;
//封装节点
root = (Bitree*)malloc(sizeof(Bitree));
if(root == NULL)
{
printf("malloc failed\n");
return NULL;
}
//数据域 左右子树地址赋值
root->data = ch;
root->left = creat_bitree();
root->right = creat_bitree();
return root;
}
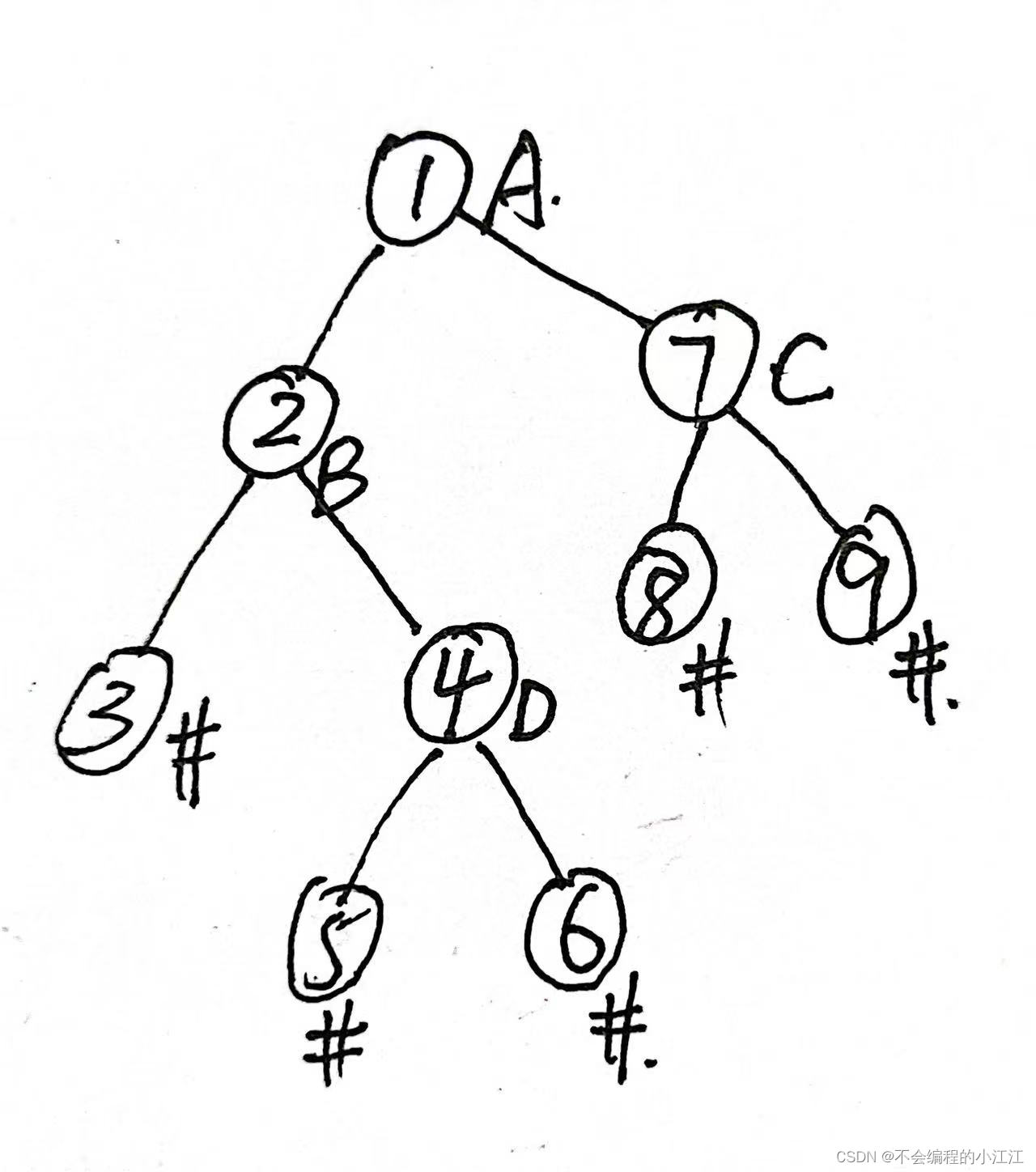
输入 AB#CD###E#FGH##K###
树模型:

遍历的C程序设计(递归)
先序遍历:
//功能:先序遍历
//参数:根节点指针
void preorder(Bitree* root)
{
if(root == NULL)
return;
//根左右
printf("%c",root->data); //获取根节点数据
preorder(root->left); //继续遍历左子树
preorder(root->right); //继续遍历右子树
}
中序遍历:
//功能:中序遍历
//参数:根节点指针
void inorder(Bitree* root)
{
if(root == NULL)
return;
//左根右
inorder(root->left);
printf("%c",root->data);
inorder(root->right);
}
后序遍历:
//功能:后序遍历
//参数:根节点指针
void postorder(Bitree* root)
{
if(root == NULL)
return ;
//左右根
postorder(root->left);
postorder(root->right);
printf("%c",root->data);
}
此时可以做一做leetcode上三道题目练练手,分别是:
关于更多二叉树的细节与进阶可参考以下几篇文章:
1. 二叉查找树(一)之 图文解析 和 C语言的实现
PS:
二叉树递归遍历过程剖析
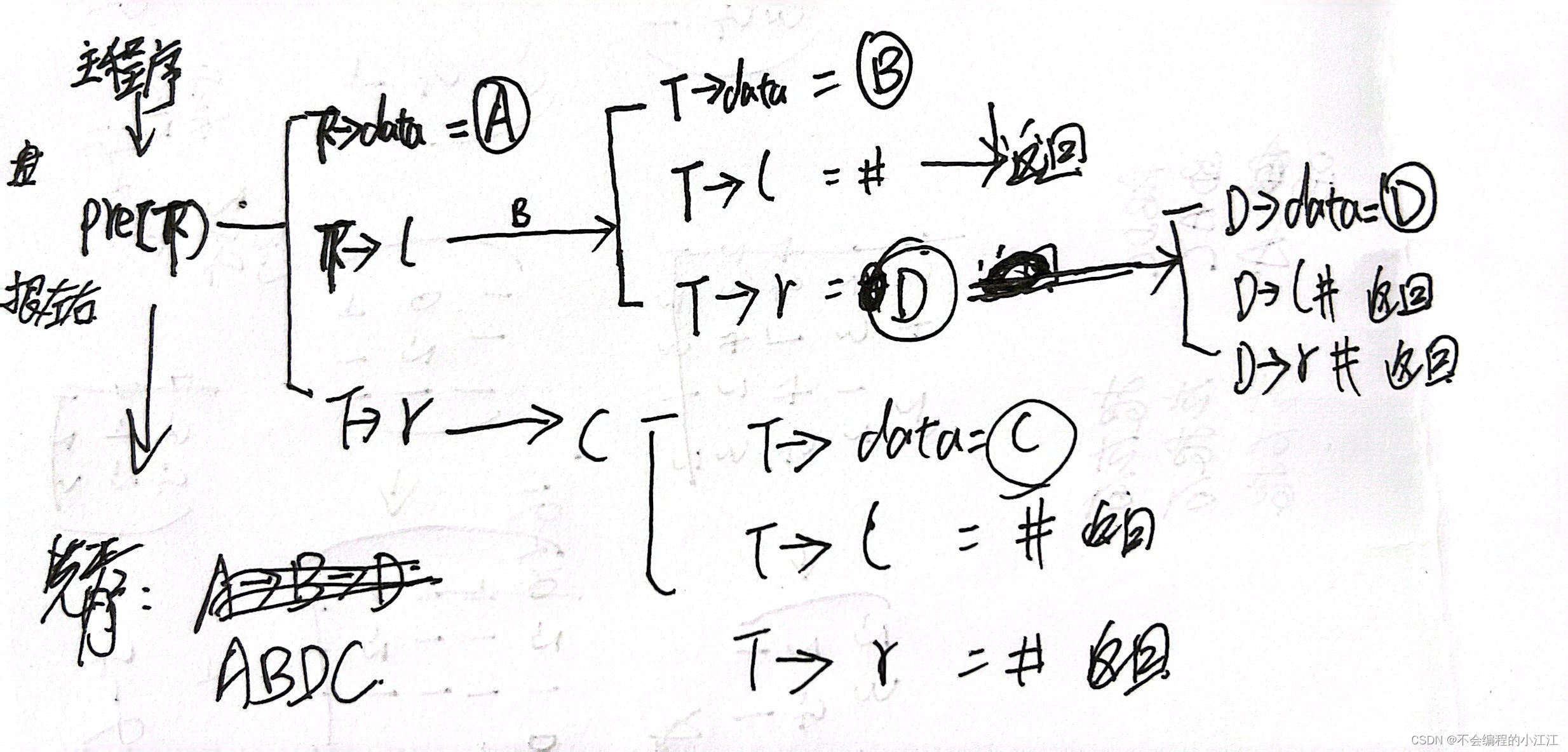
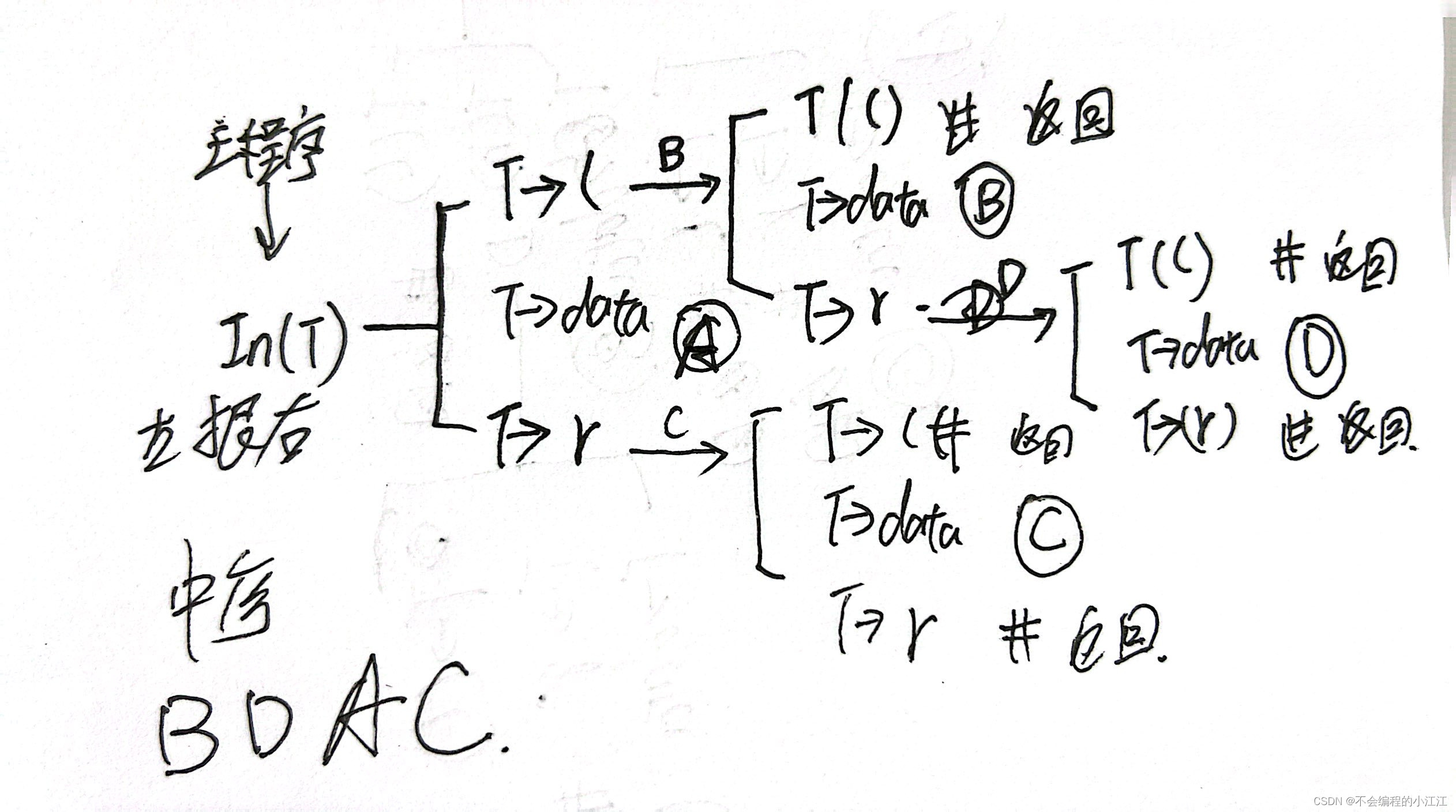
在实际学习过程中,会发现程序不难,也很短,但总觉得有点变扭与玄幻,针对这种情况,比较好的解决方法就是找一棵简单的树,在纸上完整的跑一遍递归运行的全过程,这里以一棵简单的树为例,分别手动描述先序、中序以及后续遍历的递归过程。
先序遍历:

这里也手动绘制了先序、中序、以及后序遍历的草稿过程,比较乱,仅用于当时的草稿与理解,介意乱的可跳过即可。
先序: 根左右
中序: 左中右
后续: 左右中

通过完成运行递归遍历的全过程,对树的遍历有了更深的理解与印象
树的创建过程: 其中数字表示创建的顺序,右下角为节点的值



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










