一、龙卷风优化算法
龙卷风优化算法( Tornado Optimizer with Coriolis force ,TOC) 是2025年提出的一种新型的基于自然启发的元启发式算法,其灵感来源于自然界中龙卷风的形成和演化过程。龙卷风的形成是一个复杂的自然现象,通常从雷暴或风暴中发展而来,并在地面上形成强烈的旋转气流。TOC 算法通过模拟龙卷风的形成、发展和消散过程,将其转化为优化问题中的搜索过程。

龙卷风的形成和科里奥利力
龙卷风的形成过程可以分为以下几个阶段:
- 初始阶段:在风暴系统中,风速和风向的变化会形成旋转效应,这种旋转效应在上升气流的作用下被拉直,形成旋转的气柱。
- 发展阶段:当风暴增强时,会形成超级单体雷暴(supercell thunderstorm),这种雷暴具有旋转的上升气流,是龙卷风形成的关键条件。
- 成熟阶段:当旋转的气柱与超级单体雷暴结合时,龙卷风开始形成并逐渐延伸至地面。
- 消散阶段:随着条件的变化,龙卷风逐渐变窄并逐渐升回云层,最终消散。
科里奥利力是地球自转引起的惯性力,它对大气和海洋中的大规模环流系统有重要影响。在北半球,Coriolis 力会使气流向右偏转,而在南半球则向左偏转。科里奥利力的大小与纬度和风速有关,其公式为:
∣
⃗
a
C
O
R
∣
=
f
V
|⃗a_{COR}| = fV
∣⃗aCOR∣=fV
其中,
f
f
f 是 Coriolis 参数,定义为:
f
=
2
⋅
Ω
⋅
sin
(
ϕ
)
f = 2 \cdot \Omega \cdot \sin(\phi)
f=2⋅Ω⋅sin(ϕ)
其中,
Ω
\Omega
Ω 是地球的角速度,
ϕ
\phi
ϕ 是纬度。
气旋流和梯度风
气旋流(Cyclonic flow)是指气流呈逆时针方向旋转(北半球)或顺时针方向旋转(南半球),通常与低气压系统相关。反气旋流(Anticyclonic flow)则相反,与高气压系统相关。在气旋流中,Coriolis 力和离心力(Centrifugal force, CeF)的方向相同,而压力梯度力(Pressure Gradient Force, PGF)则方向相反。其平衡关系可以表示为:
P
G
F
=
C
F
+
C
e
F
PGF = CF + CeF
PGF=CF+CeF
在反气旋流中,PGF 和 CeF 方向相同,CF 方向相反,平衡关系为:
P
G
F
+
C
e
F
−
C
F
=
0
PGF + CeF - CF = 0
PGF+CeF−CF=0
当气流的曲率半径
R
R
R 很小时,Coriolis 力可以忽略不计,此时的风速称为气旋风速(Cyclostrophic wind speed),其公式为:
V
=
−
R
∂
ϕ
∂
n
V = \sqrt{\frac{-R \partial \phi}{\partial n}}
V=∂n−R∂ϕ
其中,
∂
ϕ
/
∂
n
\partial \phi / \partial n
∂ϕ/∂n 是压力梯度力的法向分量。
梯度风近似
在实际应用中,梯度风近似(Gradient wind approximation)用于描述气流在气旋和反气旋中的运动。其公式为:
V
2
/
R
+
f
V
=
−
∂
ϕ
∂
n
V^2 / R + fV = -\frac{\partial \phi}{\partial n}
V2/R+fV=−∂n∂ϕ
解此方程可得梯度风速
V
V
V:
V
=
−
f
R
±
f
2
R
2
+
4
f
R
∂
ϕ
/
∂
n
2
V = \frac{-fR \pm \sqrt{f^2 R^2 + 4f R \partial \phi / \partial n}}{2}
V=2−fR±f2R2+4fR∂ϕ/∂n
基于科里奥利力的龙卷风优化器 (TOC)
TOC 算法是一种基于群体的优化算法,其核心思想是模拟龙卷风的形成和演化过程。算法中包含风暴(Windstorms)、雷暴(Thunderstorms)和龙卷风(Tornadoes)三种角色,它们在搜索空间中移动并相互作用,最终找到全局最优解。
TOC算法的实现步骤如下:
初始化种群:随机生成风暴、雷暴和龙卷风的位置。
适应度评估:计算每个个体的适应度值。
风速更新:根据科里奥利力和气流速度公式更新风速。
位置更新:根据风速更新个体的位置。
随机形成风暴:在搜索空间中随机生成新的风暴。
迭代终止:重复上述步骤,直到达到最大迭代次数或满足终止条件
初始化种群
TOC 算法的初始化过程是随机生成一组设计变量(风暴、雷暴和龙卷风)的位置。这些位置在搜索空间的上下界之间均匀分布。初始化公式为:
y
i
,
j
=
l
j
+
rand
×
(
u
j
−
l
j
)
y_{i,j} = l_j + \text{rand} \times (u_j - l_j)
yi,j=lj+rand×(uj−lj)
其中,
y
i
,
j
y_{i,j}
yi,j 是第
i
i
i 个个体在第
j
j
j 维的初始位置,
l
j
l_j
lj 和
u
j
u_j
uj 分别是第
j
j
j 维的下界和上界,
rand
\text{rand}
rand 是
[
0
,
1
]
[0, 1]
[0,1] 之间的随机数。
适应度评估
每个风暴、雷暴和龙卷风的适应度值通过目标函数计算得出。适应度值越小,表示该个体越接近全局最优解。适应度计算公式为:
fit
i
=
fit
(
y
i
,
1
,
y
i
,
2
,
…
,
y
i
,
d
)
\text{fit}_i = \text{fit}(y_{i,1}, y_{i,2}, \dots, y_{i,d})
fiti=fit(yi,1,yi,2,…,yi,d)
其中,
fit
i
\text{fit}_i
fiti 是第
i
i
i 个个体的适应度值,
d
d
d 是问题的维度。
风暴的演化
风暴会根据其强度和演化速度向雷暴和龙卷风移动。风暴的演化过程通过适应度值来衡量,适应度值越低的风暴越有可能演化为雷暴或龙卷风。演化过程的数学模型如下:
风暴分配到雷暴和龙卷风
根据雷暴和龙卷风的适应度值,计算每个雷暴或龙卷风分配到的风暴数量。假设
n
t
nt
nt 为雷暴数量,
n
o
no
no 为龙卷风数量,
n
w
nw
nw 为风暴数量,则有:
n
t
o
=
n
t
+
n
o
nto = nt + no
nto=nt+no
每个雷暴或龙卷风分配到的风暴数量为:
n
w
˙
k
=
⌊
f
k
∑
k
=
1
n
t
o
f
k
×
n
w
⌋
n_{\dot{w}k} = \left\lfloor \frac{f_k}{\sum_{k=1}^{nto} f_k} \times nw \right\rfloor
nw˙k=⌊∑k=1ntofkfk×nw⌋
其中,
f
k
f_k
fk 是第
k
k
k 个雷暴或龙卷风的适应度值,
⌊
⋅
⌋
\lfloor \cdot \rfloor
⌊⋅⌋ 表示向下取整。
风暴的速度更新
风暴的速度更新考虑了 Coriolis 力的影响。更新公式为:
v
⃗
t
+
1
i
=
{
η
(
μ
v
⃗
t
i
−
c
f
×
R
l
2
+
C
F
l
)
if rand
≥
0.5
η
(
μ
v
⃗
t
i
−
c
f
×
R
r
2
+
C
F
r
)
if rand
<
0.5
\vec{v}_{t+1}^{i} = \begin{cases} \eta (\mu \vec{v}_{t}^{i} - c \frac{f \times R_l}{2} + \sqrt{CF_l}) & \text{if } \text{rand} \geq 0.5 \\ \eta (\mu \vec{v}_{t}^{i} - c \frac{f \times R_r}{2} + \sqrt{CF_r}) & \text{if } \text{rand} < 0.5 \end{cases}
vt+1i={η(μvti−c2f×Rl+CFl)η(μvti−c2f×Rr+CFr)if rand≥0.5if rand<0.5
其中:
- v ⃗ t + 1 i \vec{v}_{t+1}^{i} vt+1i 是第 i i i 个风暴在第 t + 1 t+1 t+1 次迭代的速度;
- v ⃗ t i \vec{v}_{t}^{i} vti 是第 i i i 个风暴在第 t t t 次迭代的速度;
-
η
\eta
η 是收缩因子,用于控制风暴的收敛速度,其值为:
η = 2 2 − χ − χ 2 4 \eta = \frac{2}{\sqrt{2 - \chi - \frac{\chi^2}{4}}} η=2−χ−4χ22
其中, χ \chi χ 是加速因子,取值为 4.10; -
μ
\mu
μ 是模糊自适应动能因子,取值为:
μ = 0.5 + rand 2 \mu = 0.5 + \frac{\text{rand}}{2} μ=0.5+2rand -
R
l
R_l
Rl 和
R
r
R_r
Rr 分别是北半球和南半球的曲率半径,其值为:
R l = 2 1 + e − ( t − T ) / 2 , R r = − 2 1 + e − ( t − T ) / 2 R_l = \frac{2}{1 + e^{-(t-T)/2}}, \quad R_r = -\frac{2}{1 + e^{-(t-T)/2}} Rl=1+e−(t−T)/22,Rr=−1+e−(t−T)/22
其中, t t t 是当前迭代次数, T T T 是最大迭代次数; -
c
c
c 是随机因子,取值范围为:
c = b r × δ 1 × w r c = br \times \delta_1 \times wr c=br×δ1×wr
其中, b r br br 是常数,取值为 100000; δ 1 \delta_1 δ1 是符号变化因子,
参考文献
[1]Braik, M., Al-Hiary, H., Alzoubi, H. et al. Tornado optimizer with Coriolis force: a novel bio-inspired meta-heuristic algorithm for solving engineering problems. Artif Intell Rev 58, 123 (2025). https://doi.org/10.1007/s10462-025-11118-9
二、无人机(UAV)三维路径规划
单个无人机三维路径规划数学模型参考如下文献:
Phung M D , Ha Q P . Safety-enhanced UAV Path Planning with Spherical Vector-based Particle Swarm Optimization[J]. arXiv e-prints, 2021.
每个无人机的目标函数由路径长度成本,安全性与可行性成本、飞行高度成本和路径平滑成本共同组成:
2.1路径长度成本
路径长度成本由相邻两个节点之间的欧氏距离和构成,其计算公式如下:

2.2路径安全性与可行性成本

路径安全性与可行性成本通过下式计算:

2.3路径飞行高度成本

飞行高度成本通过如下公式计算所得:


2.4路径平滑成本

投影向量通过如下公式计算:

转弯角度的计算公式为:

爬坡角度的计算公式为:

平滑成本的计算公式为:

2.5总成本(目标函数)

总成本由最优路径成本,安全性与可行性成本、飞行高度成本和路径平滑成本的线性加权所得。其中,b为加权系数。
三、实验结果
在三维无人机路径规划中,无人机的路径由起点,终点以及起始点间的点共同连接而成。因此,自变量为无人机起始点间的各点坐标,每个无人机的目标函数为总成本(公式9)。本文研究3个无人机协同路径规划,总的目标函数为3个无人机的总成本之和。
%% 第一个无人机 起始点
start_location = [120;200;100];
end_location = [800;800;150];
ModelUAV(1).model.start=start_location;
ModelUAV(1).model.end=end_location;
%% 第二个无人机 起始点
start_location = [400;100;100];
end_location = [900;600;150];
ModelUAV(2).model.start=start_location;
ModelUAV(2).model.end=end_location;
%% 第三个无人机 起始点
start_location = [200;150;150];
end_location =[850;750;150];
ModelUAV(3).model.start=start_location;
ModelUAV(3).model.end=end_location;
%% 第四个无人机 起始点
start_location = [100;100;150];
end_location = [800;730;150];
ModelUAV(4).model.start=start_location;
ModelUAV(4).model.end=end_location;
%% 第5个无人机 起始点
start_location = [500;100;130];
end_location = [850;650;150];
ModelUAV(5).model.start=start_location;
ModelUAV(5).model.end=end_location;
figure
plot(Convergence_curve,'LineWidth',2)
xlabel('Iteration');
ylabel('Best Cost');
grid on;
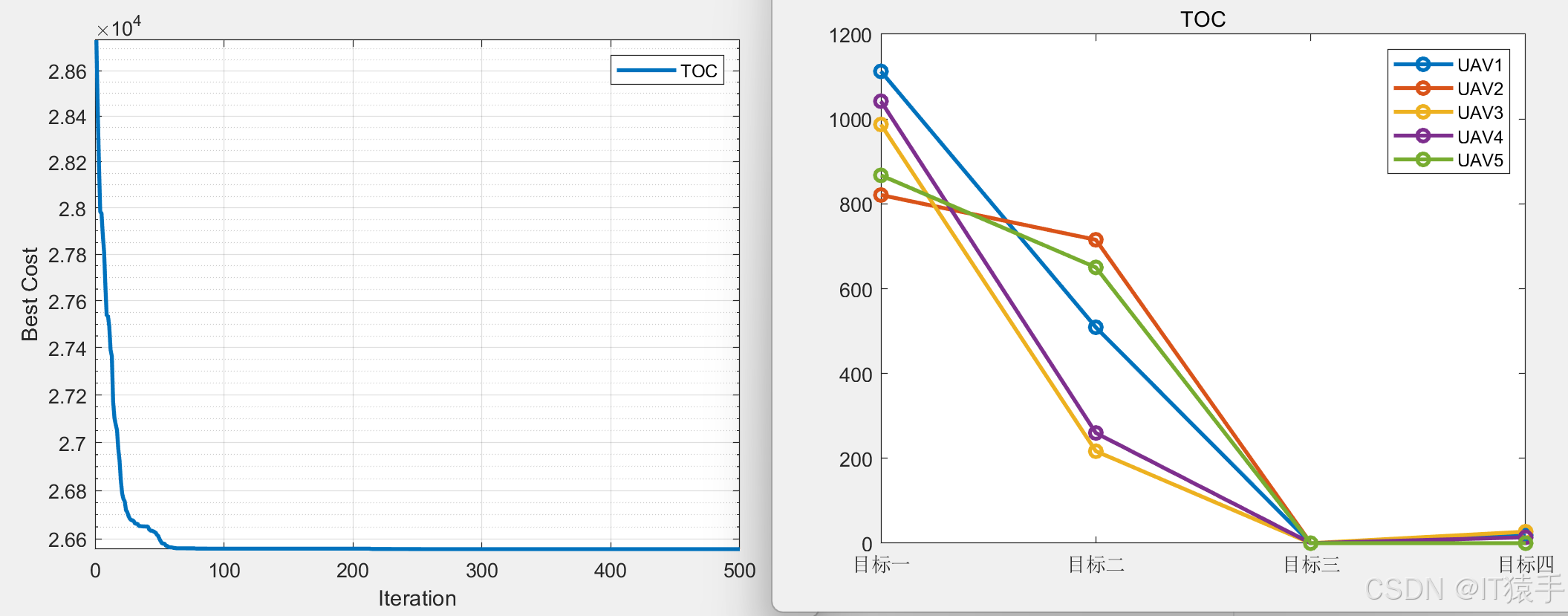
五个无人机:


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








