数据结构之折半查找

折半查找的算法思想：

折半查找又称二分查找，它仅仅适用于有序的顺表。
折半查找的基本思想：首先将给定值key与表中中间位置的元素（mid的指向元素）比较。mid=low+high/2（向下取整）

1. 若key与中间元素相等，则查找成功，返回该元素的存储位置，即mid；
2. 若key与中间元素不相等，则所需查找的元素只能在中间元素以外的前半部分或后半部分。（至于是前半部分还是后半部分要看key与mid所指向元素的大小关系）
   a.在查找表升序排列的情况下，若给定值key大于中间元素则所查找的元素只可能在后半部分。此时让low=mid+1；
   b.若给定值key小于中间元素则所查找的元素只可能在前半部分。此时让high=mid-1；

来到题目练练手：

初始化low=0，high=10。
第一轮：mid=(low+high）/2=5,即mid指向5号位置。查找目标为33，key大于mid，所以如果33元素存在的话一定在此时mid的右边。因为key大于mid，所以更新low=mid+1；即low=6，high不变。
第二轮：mid=(low+high）/2=8，即mid指向8号位置.查找目标小于mid所指向的值，所以查找元素若存在一定在mid的左边。更新high=mid-1=7；low不变。
第三轮：mid=(low+high）/2=6，即mid指向6号位置，查找目标大于mid所指向的值，更新low=mid+1=7；high不变。
第四轮：mid=(low+high）/2=7，即mid指向6号位置，查找元素等于id所指向的值。查找成功！返回7。

折半查找的代码实现

/*查找表的数据结构（顺序表），因为链表不具备随机存取的特性，
链表不能用链表来实现*/
typedef struct{		
	ElemType *elem;	//动态数组基址
	int TableLen;	//表的长度
}SSTable;

//折半查找
int Binary_Search(SSTable L,ElemType key){
	int low=0,high=L.TableLen-1,mid;
	while(low<=high){
		mid=(low+high)/2;		//取中间位置
		if(L.elem[mid]==key)	
			return mid;			//查找成功返回所在的位置
		else if(L.elem[mid]>key){	//从前部分查找
			high=mid-1;
		}
		else
			low=mid+1;		//从后部分查找
	}
	return -1;				//查找失败，返回-1
}

折半查找判定树的构造

如果当前low和high之前有奇数个元素，则mid分隔后，左右两部分元素个数相等。

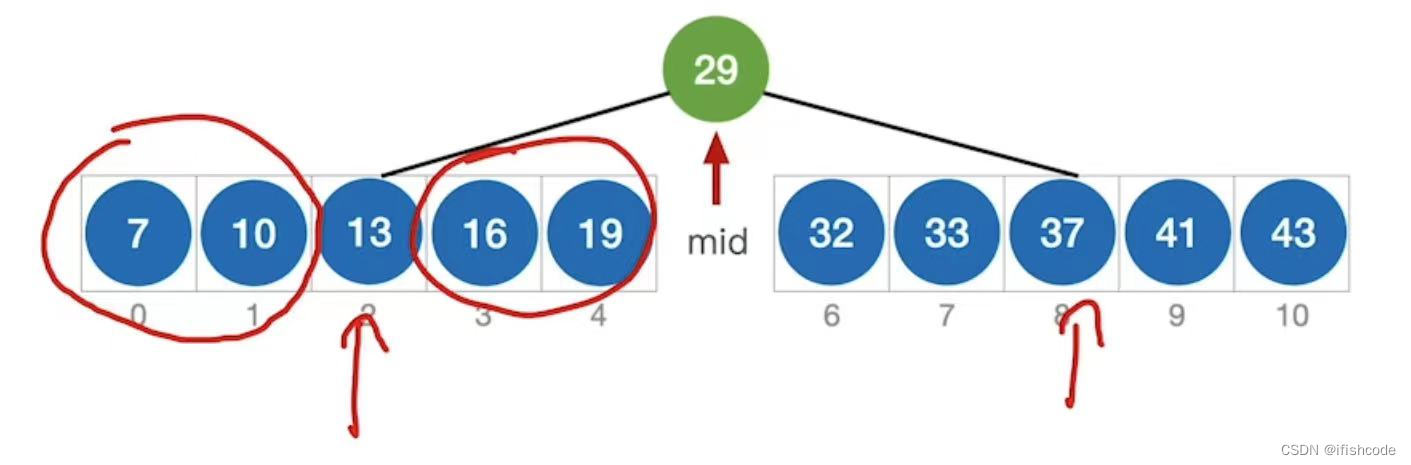
如果当前low和high之间有偶数个元素，则mid分隔后，左半部分比右半部分少一个元素



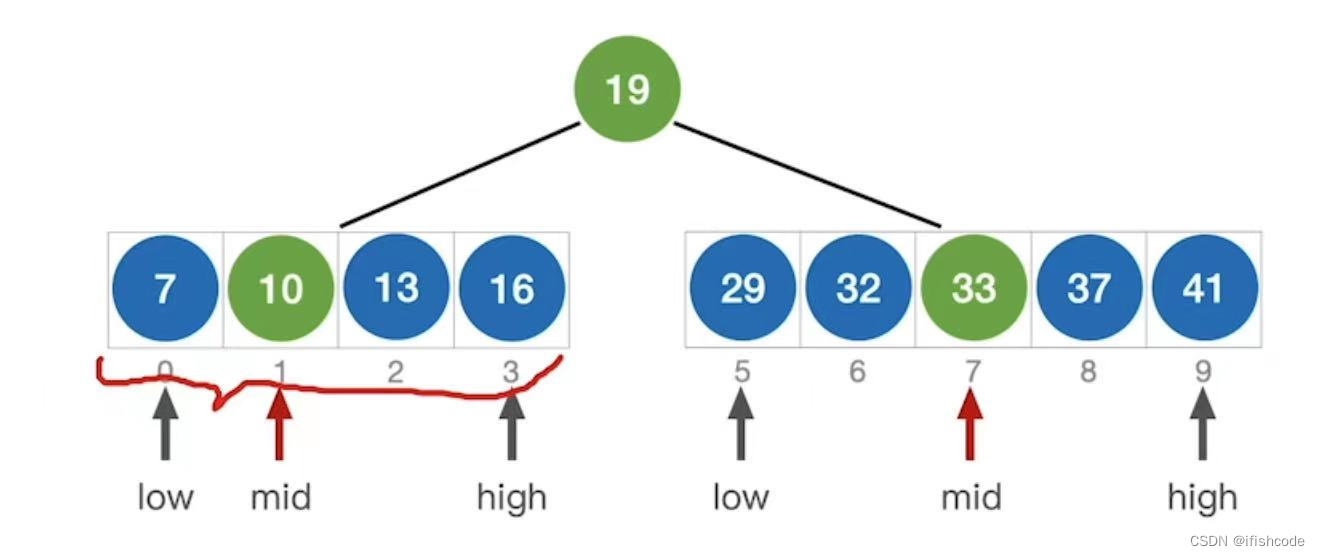
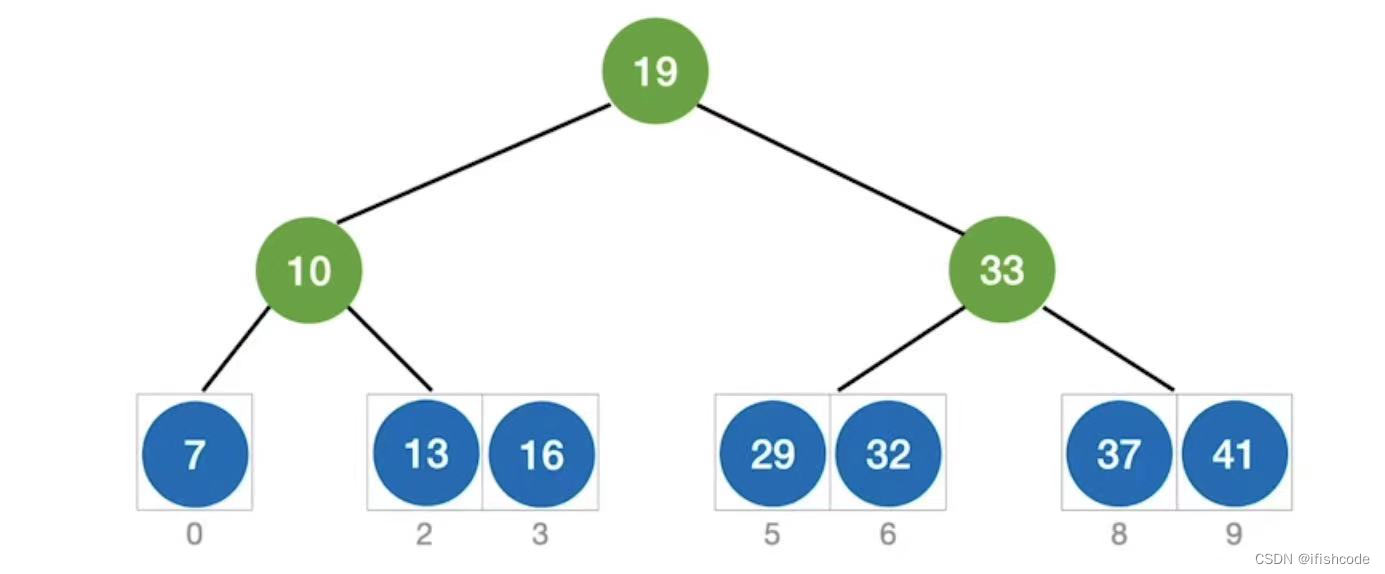
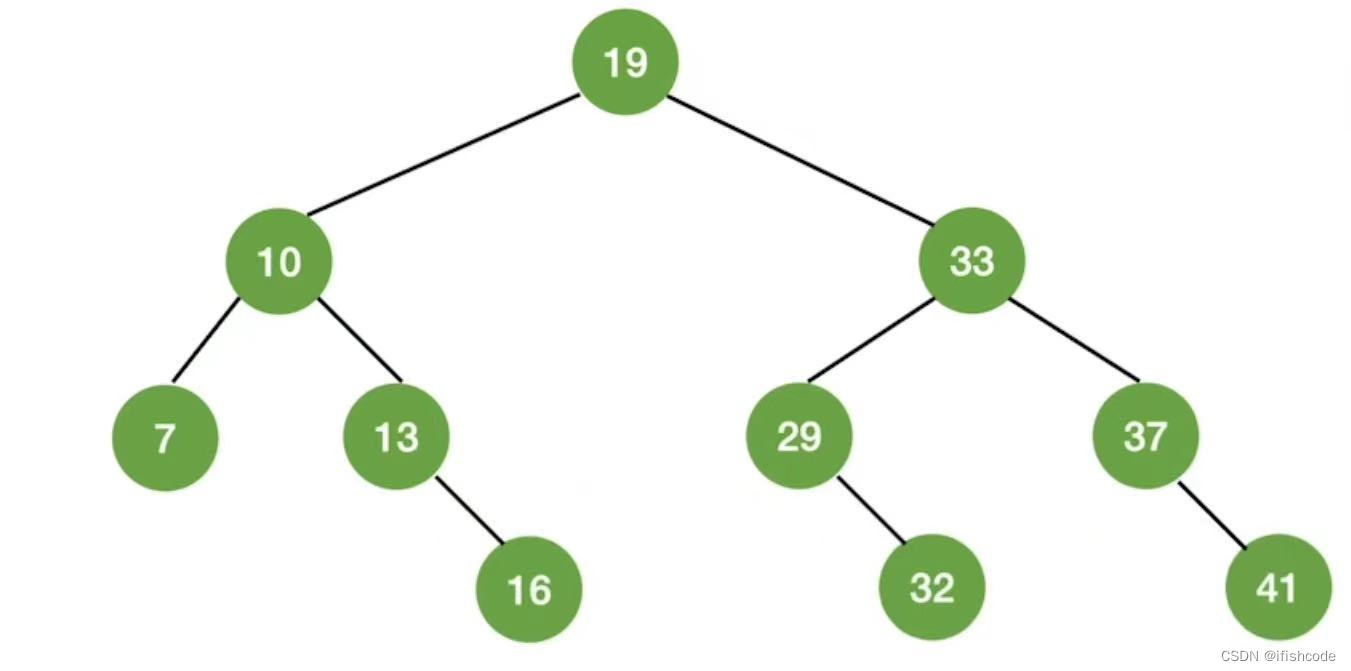
可以得出结论：
如果当前low和high之间有奇数个元素，则mid分隔后，左右两部分元素个数相等。
如果当前low和high之间有偶数个元素，则mid分隔后，左边部分比右半边部分少一个元素。
在折半查找的判定树中，若mid=（low+high）/2，向下取整，则对于任何一个结点，必有：右子树结点-左子树结点数=0或1。当有奇数个元素时等于0，有偶数个元素时等于1。所以折半查找判定数一定是平衡二叉树。
此外判定树结点关键字：左结点<中<右结点。满足二叉排序树的定义

顺序查找是对着查找表一个元素一个元素查找下去，它的时间复杂度=O(n)。
很显然这折半查找在大多数情况下比顺序查找更有效率。所以我们可以联想记忆：折半查找的时间复杂度为O(log2n)。

那什么情况下顺序查找比折半查找速度更快？
答：在查找元素在表的第一个结点时，顺序查找可以一下子就找到该元素。

若有纰漏之处，欢迎评判指正！