Opencv图像梯度计算
Sobel算子
可以理解为是做边缘检测的一种方法。
首先说明自己对图像梯度的简单理解:简单理解就是图像的颜色发生变化的边界区域在X方向和Y方向上的梯度值 Gx Gy
而Gx和Gy处的梯度的计算—使用下面的公式来进行计算。
Gx=[−10+1−20+2−10+1]∗A and Gy=[−1−2−1000+1+2+1]∗A \mathbf{G}_{x}=\left[\begin{array}{lll} -1 & 0 & +1 \\ -2 & 0 & +2 \\ -1 & 0 & +1 \end{array}\right] * \mathbf{A} \quad \text { and } \quad \mathbf{G}_{y}=\left[\begin{array}{ccc} -1 & -2 & -1 \\ 0 & 0 & 0 \\ +1 & +2 & +1 \end{array}\right] * \mathbf{A} Gx=−1−2−1000+1+2+1∗A and Gy=−10+1−20+2−10+1∗A
在Opencv中使用函数调用的方法为:
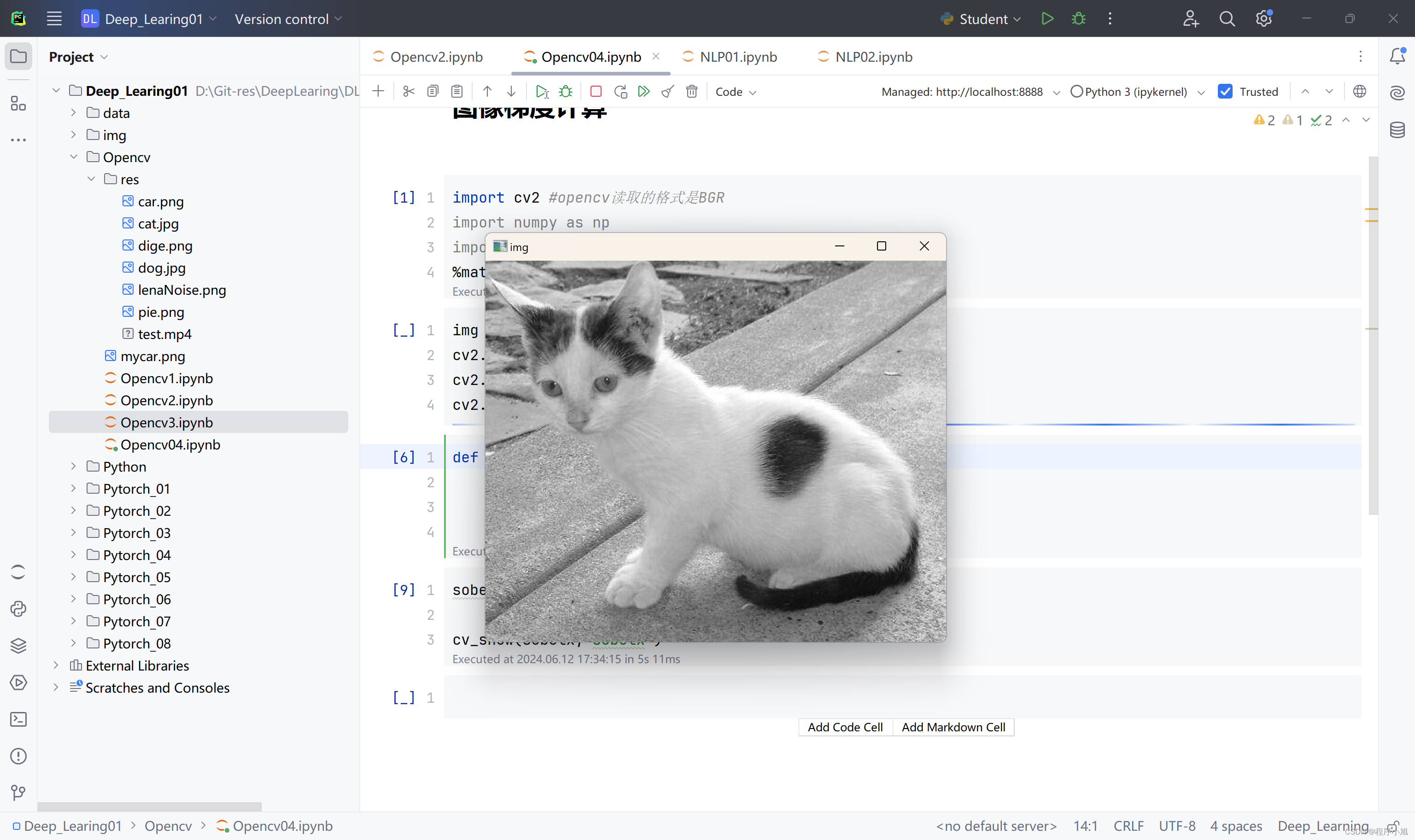
img = cv2.imread('./res/cat.jpg',cv2.IMREAD_GRAYSCALE)
cv2.imshow("img",img)
cv2.waitKey()
cv2.destroyAllWindows()
dst = cv2.Sobel(src, ddepth, dx, dy, ksize)
- ddepth:图像的深度
- dx和dy分别表示水平和竖直方向
- ksize是Sobel算子的大小
def cv_show(img,name):
cv2.imshow(name,img)
cv2.waitKey()
cv2.destroyAllWindows()
#%%
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
cv_show(sobelx,'sobelx')
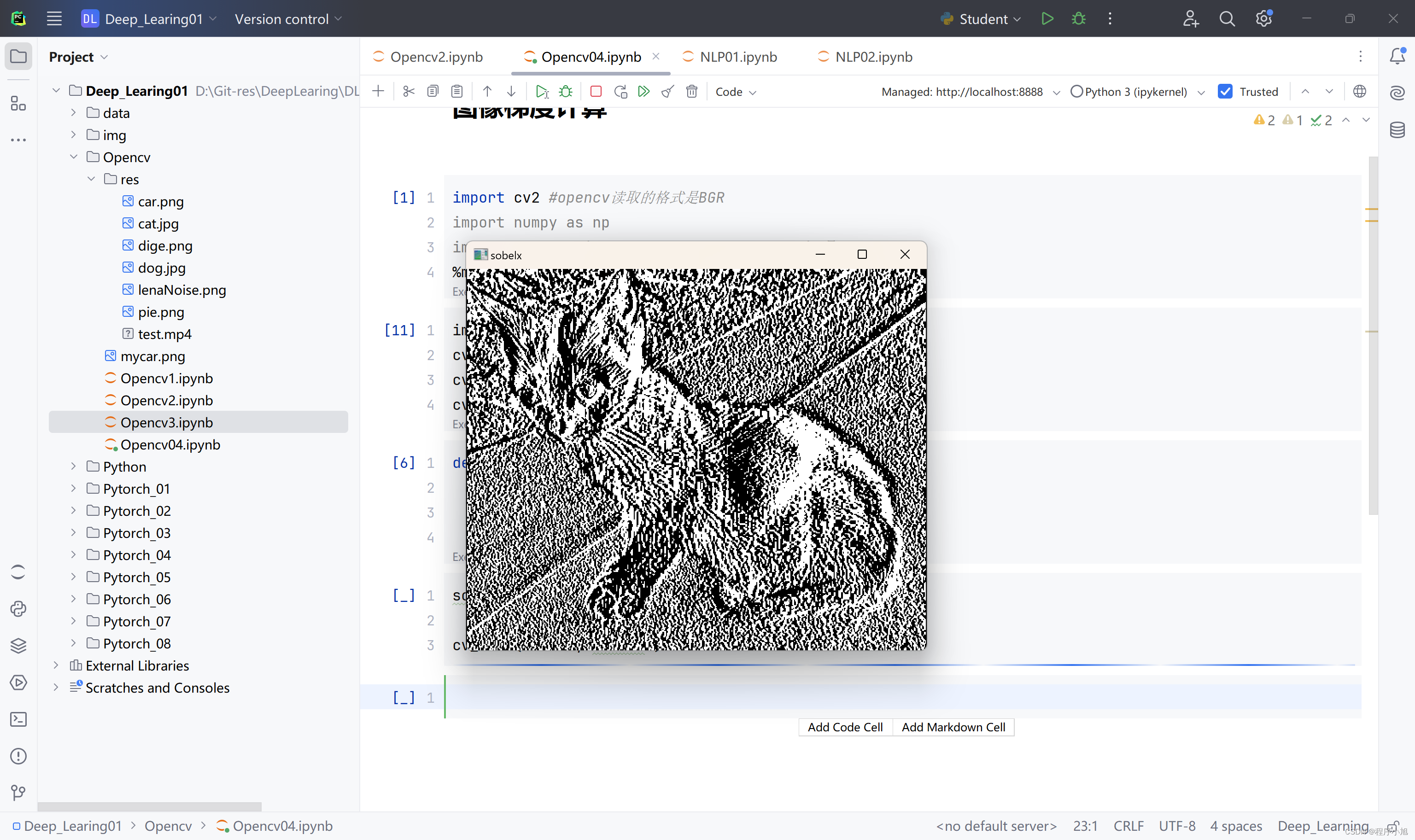
使用Sobel算子进行计算相当于提取边缘的一种方式。白到黑是正数,黑到白就是负数了,所有的负数会被截断成0,所以要取绝对值对右侧区域进行补充
(1,0)代表X轴的方向 (0,1)代表的是Y轴的方向
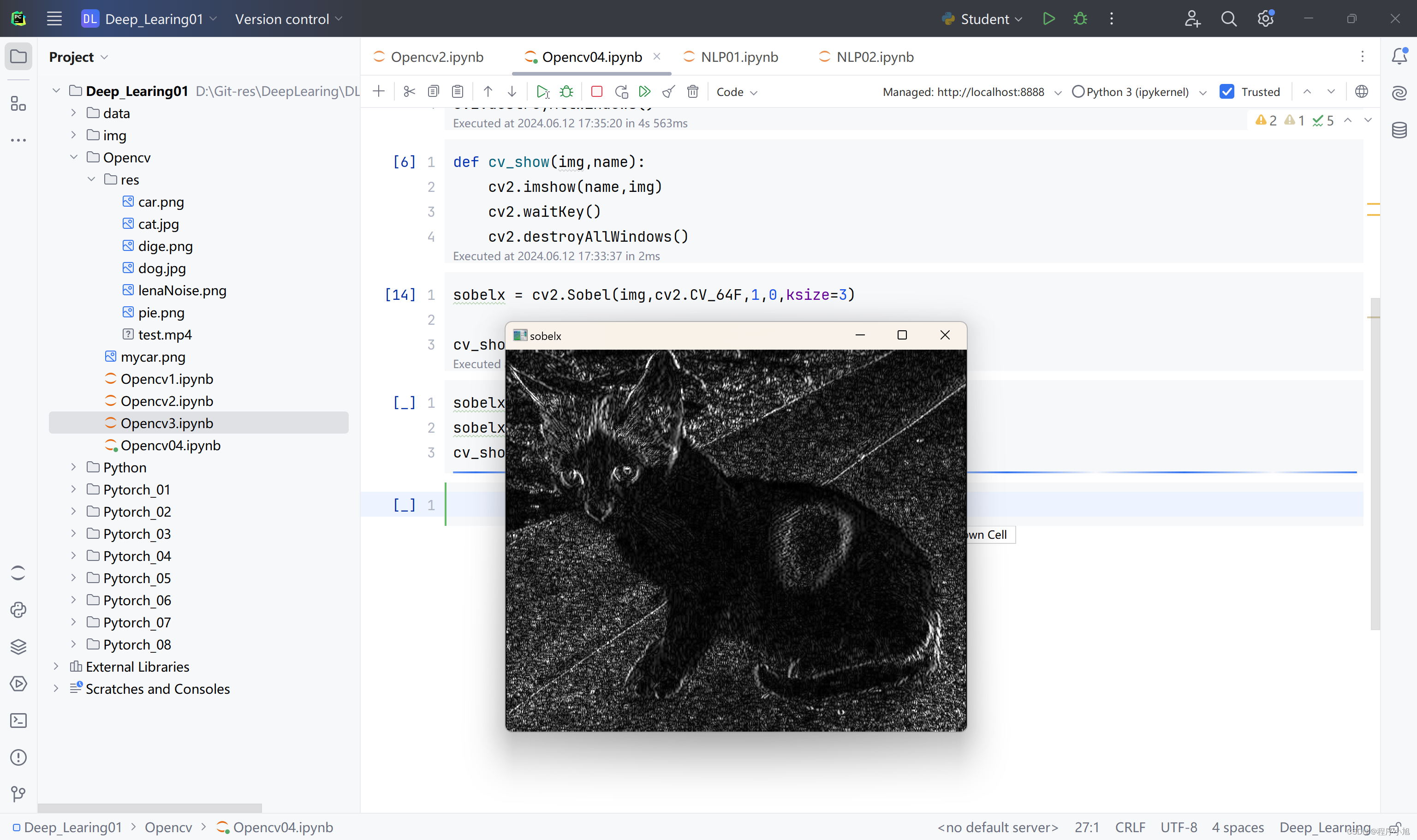
sobelx = cv2.Sobel(img,cv2.CV_64F,1,0,ksize=3)
sobelx = cv2.convertScaleAbs(sobelx)
cv_show(sobelx,'sobelx')
sobely = cv2.Sobel(img,cv2.CV_64F,0,1,ksize=3)
sobely = cv2.convertScaleAbs(sobely)
cv_show(sobely,'sobely')
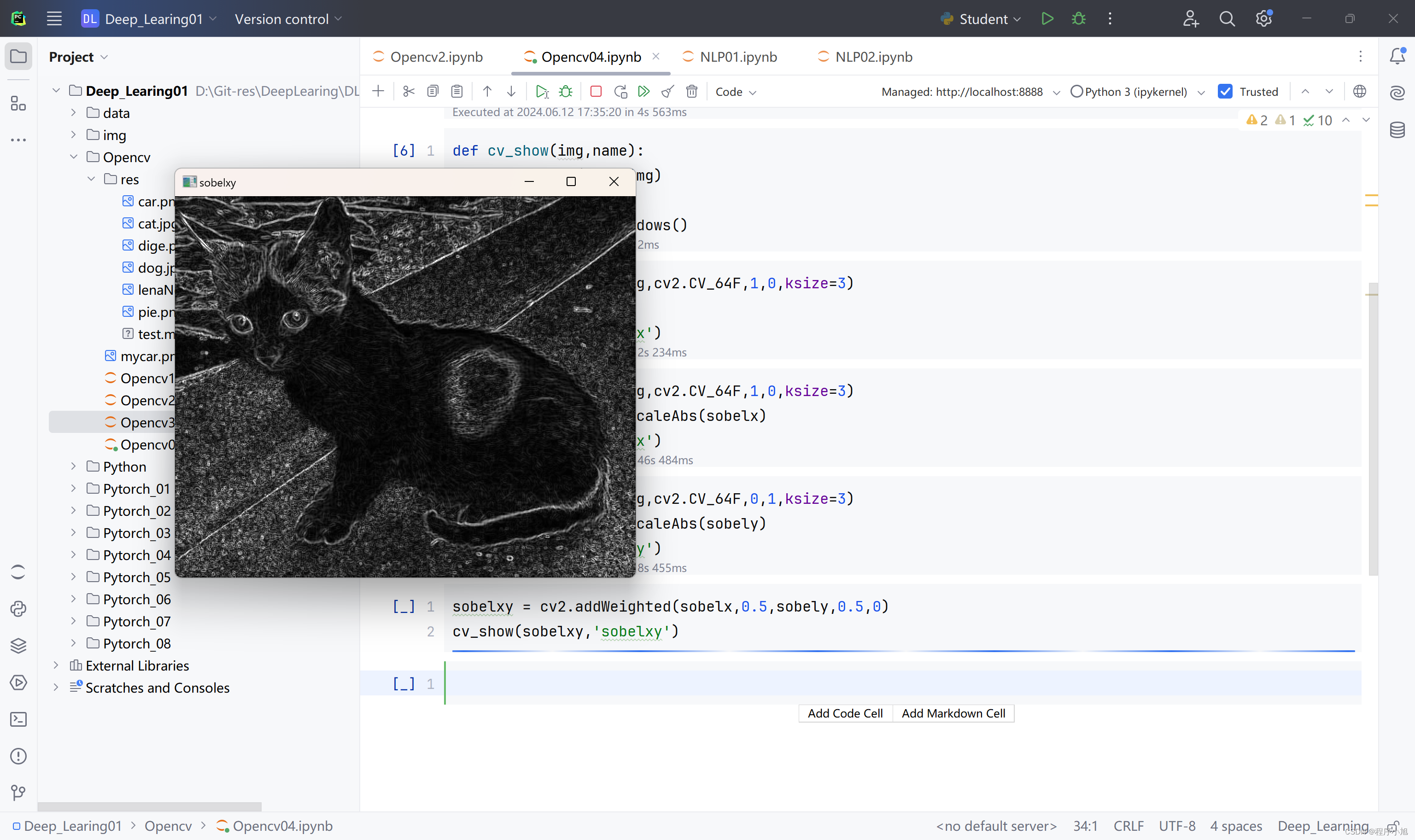
计算综合值:将GX的平方与Gy的平方相加之后开根号进行计算得到最终图像的处理效果。
sobelxy = cv2.addWeighted(sobelx,0.5,sobely,0.5,0)
cv_show(sobelxy,'sobelxy')

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










