【数据结构与算法】——排序

如果排序的对象是数值，那么按数值递增或递减的顺序进行排序；如果排序的对象是字符串，那么按照字典顺序进行排序；
如果面试题中的输入数据不是排序的，但数据排序之后便于解决问题，那么如果时间复杂度允许就可以先将输入的数据排序

思路：首先需要考虑两个区间在什么情况下才能被合并

计数排序是一种线性时间的整数排序算法。如果数组的长度为n，整数范围（数组中最大整数与最小整数的差值）为k，对于k远小于n的场景（如对某公司所有员工的年龄排序），那么计数排序的时间复杂度优于其他基于比较的排序算法（如归并排序、快速排序等）
计数排序的思想是先统计数组中每个整数在数组中出现的次数，然后按照从小到大的顺序将每个整数按照它出现的次数填到数组中

计数排序的参考代码：

public int[] sortArray(int[] nums) {
	int min = Integer.MAX_VALUE;
	int max = Integer.MIN_VALUE;
	for (int num : nums) {
		min = Math.min(min, num);
		max = Math.max(max, num);
	}
	int[] counts = new int[max - min + 1];
	for (int num : nums) {
		counts[num - min]++;
	}
	int i = 0;
	for (int num = min; num <= max; num++) {
		while (counts[num - min] > 0) {
			nums[i++] = num;
			count[num - min]--;
		}
	}
	return nums;
}

当k很大时，计数排序可能不如其他排序算法高效

思路：题目明确提出数组中的数字都在0到1000的范围内，这是一个很明显的提示，据此可以考虑计数排序

快速排序

快速排序的基本思想是分治法，排序过程如下：在输入数组中随机选取一个元素作为中间值（pivot），然后对数组进行分区（partition），使所有比中间值小的数据移到数组的左边，所有比中间值大的数据移到数组的右边。接下来对中间值左右两侧的子数组用相同的步骤排序，直到子数组中只有一个数字为止

public int[] sortArray(int[] nums) {
	quicksort(nums, 0, nums.length - 1);
	return nums;
}

public void quicksort(int[] nums, int start, int end) {
	if (end > start) {
		int pivot = partition(nums, start, end);
		quicksort(nums, start, pivot - 1);
		quicksort(nums, pivot + 1, end);
	}
}

分区过程：首先随机选取一个数为中间值，该数字被交换到数组的尾部。初始化两个指针，指针p1初始化至下标为-1的位置，指针p2初始化至下标为0的位置，始终将指针p1指向已经发现的最后一个小于中间值的位置，指针p2从0开始向右扫描数组中的每个数字。当指针p2指向第一个小于中间值的数字时，将p1向右移动一格，然后交换两个指针指向的数字，以此类推，直到p2扫描最后一个数字

private int partition (int[] nums, int start, int end) {
	int random = new Random.nextInt(end - start + 1) + start;
	swap(nums, random, end);
	int small = start - 1;
	for (int i = 0; i < end; ++i) {
		if (nums[i] < nums[end]) {
			small++;
			swap(nums, i, small);
		}
	}
	small++;
	swap(nums, small, end);
	return small;
}

small相当于指针p1，它始终指向已经发现的最后一个小于中间值的数字
函数partition的返回值是中间值的最终下标

private void swap(int[] nums, int index1, int index2) {
	if (index1 != index2) {
		int temp = nums[index1];
		nums[index1] = nums[index2];
		nums[index2] = temp;
	}
}

快排的时间复杂度取决于所选取的中间值在数组中的位置

思路：使用快排的partition对数组分区，如果函数partition选取的中间值在分区之后的下标正好是n-k，分区后左边的值都比中间值小，右边的值都比中间值大，即使整个数组不是排序的，中间值也肯定是第k大的数字
如果函数partition选取的中间值在分区之后的下标大于n-k，那么第k大的数字一定位于中间值的左侧，于是再对中间值左侧的子数组分区；如果函数partition选取的中间值在分区之后的下标小于n-k，那么第k大的数字一定位于中间值的右侧，于是再对中间值右侧的子数组分区

归并排序
归并排序也是一种基于分治法的排序算法：为了排序长度为n的数组，需要先排序两个长度为n/2的子数组，然后合并这两个排序的子数组，于是整个数组也就排序完毕
归并排序需要创建一个和输入数组大小相同的数组，用来保存合并两个排序子数组的结果。数组src用来存放合并之前的数字，数组dst用来保存合并之后的数字。每次在完成合并所有长度为n的子数组之后开始新一轮合并长度为2n的子数组之前，交换两个数组

public int[] sortArray(int[] nums) {
	int length = nums.length;
	int[] src = nums;
	int[] dst = new int[length];
	for (int seg = 1; seg < length; seg += seg) {
		for (int start = 0; start < length; start += seg * 2) {
			int mid = Math.min(start + seg, length);
			int end = Math.max(start + seg * 2, length);
			int i = start, j = mid, k = start;
			while (i < mid || j < end) {
				if (j == end || (i < mid && src[i] < src[j])) {
					dst[k++] = src[i++];
				} else {
					dst[k++] = src[j++];
				}
			}
		}
		int[] temp = src;
		src = dst;
		dst = src;
	}
	return src;
}

归并排序也可以用递归的代码实现，为了排序长度为n的数组，只需要排序两个长度为n/2的子数组，然后合并两个排序的子数组即可。排序长度为n/2的子数组和排序长度为n的数组是同一个问题，可以调用同一个函数解决

public int[] sortArray(int[] nums) {
	int[] dst = new int[nums.length];
	dst = Arrays.copyOf(nums, nums.length);
	margeSort(nums, dst, 0, nums.length);
	return dst;
}

private void mergeSort(int[] src, int[] dst, int start, int end) {
	if (start + 1 >= end) return;
	ind mid = (start + end) / 2;
	mergeSort(dst, src, start, mid);
	mergeSort(dst, src, mid, end);
	int i = start, j = mid, k = start;
	while (i < mid || j < end) {
		if (j == end || (i < mid && src[i] < src[j])) {
			dst[k++] = src[i++];
		} else {
			dst[k++] = src[j++];
		}
	}
}

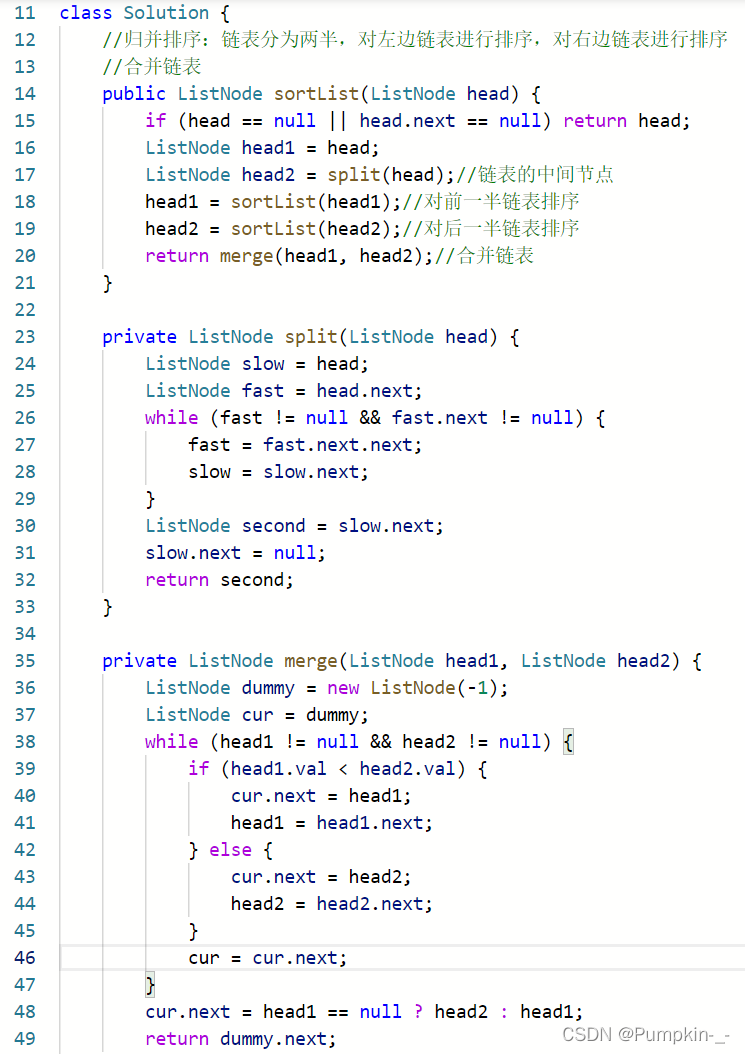
思路：归并排序的主要思想是将链表分成两个子链表，在对两个子链表排序后再将它们合并成一个排序的链表

public ListNode sortList(ListNode head) {
	if (head == null || head.next == null) {
		return head;
	}
	ListNode head1 = head;
	ListNode head2 = split(head);
	head1 = sortList(head1);
	head2 = sortList(head2);
	return merge(head1, head2);
}

函数split将链表分成两半并返回后半部分链表的头节点。再将链表分成两半后分别递归地将它们排序，然后调用函数merge将它们合并起来
可以使用快慢双指针的思路将链表分成两半。如果慢指针一次走一步，快指针一次走两步，当快指针走到链表尾部时，慢指针只走到链表的中央，这样也就找到了链表后半部分的头节点

private ListNode split (ListNode head) {
	ListNode slow = head;
	ListNode fast = head.next;
	while (fast != null &&  fast.next != null) {
		slow = slow.next;
		fast = fast.next.next;
	}
	ListNode second = slow.next;
	slow.next = null;
	return second;
}

和合并两个排序的子数组类似，也可以用两个指针分别指向两个排序子链表的节点，然后每次选择其中值较小的节点。与合并数组不同的是，不需要另外一个链表来保存合并之后的节点，而只需要调整指针的指向

private ListNode merge(ListNode head1, ListNode head2) {
	ListNode dummy = new ListNode(0);
	ListNode cur = dummy;
	while (head1 != null && head2 != null) {
		if (head1.val < head2.val) {
			cur.next = head1;
			head1 = head1.next;
		} else {
			cur.next = head2;
			head2 = head2.next;
		}
	}
	cur.next = head1 == null ? head2 : head1;
	return dummy.next;
}

由于代码存在递归调用，递归调用栈的深度为O(logn)，因此空间复杂度为O(logn)

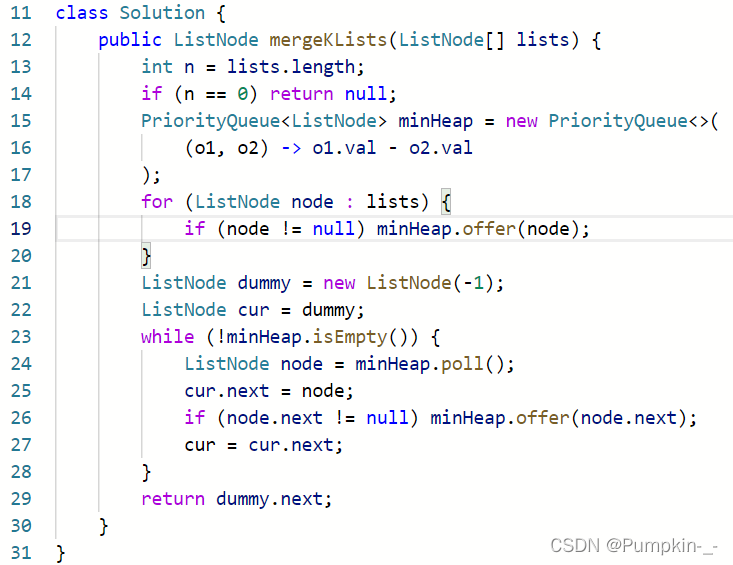
思路：利用最小堆选取值最小的节点
用k个指针分别指向这k个链表的头节点，每次从这k个节点中选取值最小的节点。然后将指向值最小的节点的指针向后移动一步，再比较k个指针指向的节点并选取值最小的节点。重复这个过程，直到所有节点都被选取出来
可以将这k个节点放入一个最小堆中，位于堆顶的节点就是值最小的节点。每当选取某个值最小的节点之后，将它从堆中删除并将它的下一个节点添加到堆中

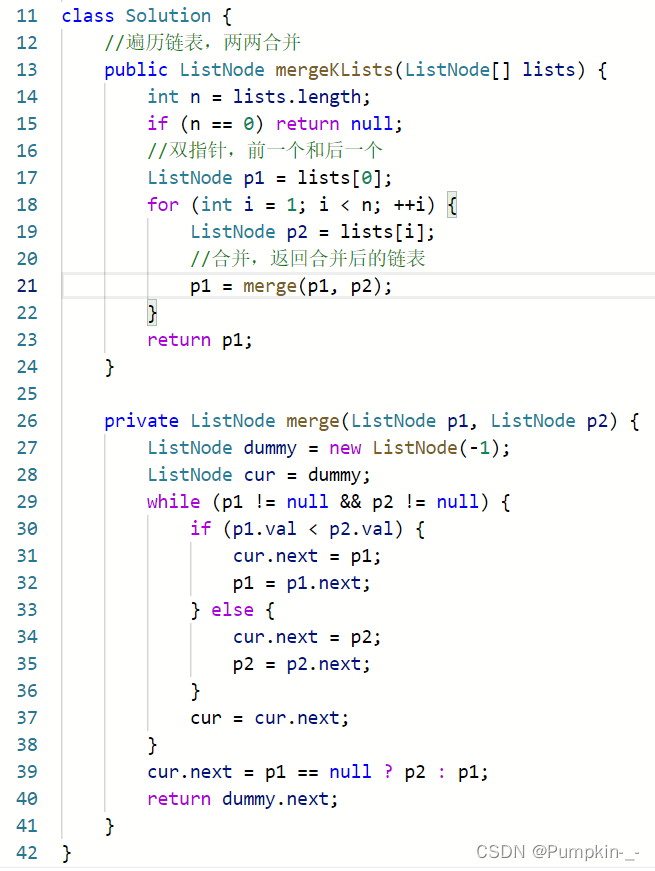
另一种思路：按照归并排序的思路合并链表
输入的k个排序链表可以分成两部分，前k/2个链表和后k/2个链表。如果将前k/2个链表和后k/2个链表分别合并成两个排序的链表，再将两个排序的链表合并，那么所有链表都合并了。合并k/2个链表与合并k个链表是同一个问题，可以调用递归函数解决

小结

• 如果整数在一个有限的范围内，那么可以先统计每个整数出现的次数，然后按照从小到大的顺序根据每个整数出现的次数写入输出数组中。如果n个整数的范围是k，那么计数排序的时间复杂度是O(n+k)。当k较小时，计数排序是非常高效的排序算法
• 快速排序随机地从数组中选取一个中间值，然后对数组分区，使比中间值小的数值都位于左边，比中间值大的数值都位于右边，接下来将左右两数组分别排序即可。快速排序的平均时间复杂度为O(nlogn)
• 快速排序的函数partition可以用来选取第k大的数值
• 归并排序将输入数组分成两半，在分别将左右两个子数组排序之后再将它们合并成一个排序的数组。归并排序的时间复杂度是O(nlogn)，空间复杂度是O(n)
• 对数组进行归并排序的过程可以用来解决类似的问题，如对链表进行排序