【力扣一刷】代码随想录day14（二叉树理论基础、 递归遍历 、 迭代遍历、统一迭代）

已于 2024-03-26 15:59:05 修改
阅读量739 收藏 19
点赞数 8
分类专栏： 力扣一刷打卡日记 文章标签： 深度优先 宽度优先 算法
于 2024-03-20 01:49:36 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/weixin_46135891/article/details/136824602
版权
本文详细介绍了二叉树的基本概念，包括满二叉树、完全二叉树和二叉搜索树的定义，以及顺序存储和链式存储两种方式。重点讲解了递归和迭代遍历方法，特别是统一迭代在前序、中序和后序遍历中的应用，以及Java中二叉树节点的定义和实现。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

【二叉树理论基础】

一、二叉树的形式

1、满二叉树

2、完全二叉树

3、二叉搜索树（有序树）

4、平衡二叉搜索树

二、二叉树的存储方式

1、顺序存储

2、链式存储

三、二叉树的遍历方式

四、二叉树节点定义的Java实现

【递归遍历】

144. 二叉树的前序遍历

94. 二叉树的中序遍历

145. 二叉树的后序遍历

【迭代遍历】

144. 二叉树的前序遍历

94. 二叉树的中序遍历

145. 二叉树的后序遍历

【统一迭代】

144. 二叉树的前序遍历

方法一  学完中序的统一迭代后，自己写的（进步很大拉！），但思路有点不太一样。

方法二  按照统一迭代思路（更简单）

94. 二叉树的中序遍历

145. 二叉树的后序遍历

【二叉树理论基础】

一、二叉树的形式

1、满二叉树

  • 定义：只有度为0的结点和度为2的结点，并且度为0的结点在同一层上，则这棵二叉树为满二叉树。
  • 深度：k
  • 节点个数：2^k-1

2、完全二叉树

定义：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。

3、二叉搜索树（有序树）

规则：

  • 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
  • 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
  • 它的左、右子树也分别为二叉排序树

4、平衡二叉搜索树

规则：

  • 它是一棵空树或它的左右两个子树的高度差的绝对值不超过1；
  • 左右两个子树也都是一棵平衡二叉树。

二、二叉树的存储方式

1、顺序存储

  • 介绍：顺序存储实际上就是用数组存储。
  • 节点和数组下标的关系：如果根节点的数组下标是 i，那么它的左节点就是 i * 2 + 1，右节点就是 i * 2 + 2。

2、链式存储

三、二叉树的遍历方式

  • 深度优先遍历
    • 前序遍历（递归法，迭代法）
    • 中序遍历（递归法，迭代法）
    • 后序遍历（递归法，迭代法）
  • 广度优先遍历
    • 层次遍历（迭代法）

深度优先遍历：中间节点的顺序 = 所谓的遍历方式

  • 前序遍历：中左右
  • 中序遍历：左中右
  • 后序遍历：左右中

四、二叉树节点定义的Java实现

public class TreeNode{
    int val;
    TreeNode left;
    TreeNode right;

    // 无参构造器
    public TreeNode(){}

    // 只有值的构造器
    public TreeNode(int val) this.val = val;
    
    // 全参构造器
    public TreeNode(int val, TreeNode left, TreeNode right){
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

【递归遍历】

144. 二叉树的前序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        preorder(root, result); // 需要传入根节点和记录遍历结果的数组，不需要返回值
        return result;
    }

    public void preorder(TreeNode node, List<Integer> result){
        if (node == null) return; // 终止条件
        result.add(node.val);  // 中
        preorder(node.left, result);  //左 
        preorder(node.right, result);  // 右
    }
}

94. 二叉树的中序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        postorder(root, result);
        return result;
    }

    public void postorder(TreeNode node, List<Integer> result){
        if (node == null) return;

        postorder(node.left, result);  // 左
        result.add(node.val);  // 中
        postorder(node.right, result);  // 右
    }
}

145. 二叉树的后序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        inorder(root, result);
        return result;
    }

    public void inorder(TreeNode node, List<Integer> result){
        if (node == null) return;

        inorder(node.left, result);  // 左
        inorder(node.right, result);  // 右 
        result.add(node.val);  // 中
    }
}

【迭代遍历】

144. 二叉树的前序遍历

思路：中前后，先记录中间节点，再将右节点和左节点依次压入栈

注意：右节点比左节点先入栈，是为了先让左节点弹出

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<TreeNode> stack = new ArrayDeque<>();
        
        // 必须判断root是否为空，否则后续会报错
        if (root == null) return result;

        TreeNode cur = root;
        stack.push(root);  // 先将中节点压入栈
        while (!stack.isEmpty()){
            cur = stack.pop();
            result.add(cur.val); // 先记录中节点
            if (cur.right != null) stack.push(cur.right); // 将右节点压入栈
            if (cur.left != null) stack.push(cur.left);  // 再将左节点压入栈（为了先弹出左节点）
        }
        return result;
    }
}

94. 二叉树的中序遍历

思路：左中右，只要不为空就先访问左子树

1、当前节点不为空，则压入栈，继续访问左子树（左）

2、当前节点为空，栈弹出元素并保存到result集合（中），继续访问右子树（右）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<TreeNode> stack = new ArrayDeque<>();

        TreeNode cur = root;
        
        // 开始状态：stack的初始为空，要多增加一个条件（cur != null）才能让循环开始
        // 结束状态：stack为空，且cur为空，则无法继续弹出栈顶，需要结束循环
        while (cur != null || !stack.isEmpty()){
            // 1、当前节点不为空，则压入栈，继续访问左子树
            if (cur != null){
                stack.push(cur);
                cur = cur.left;  // 继续访问左子树
            }
            // 2、当前节点为空，栈弹出元素并保存到result集合，继续访问右子树
            else{
                cur = stack.pop();
                result.add(cur.val);  // 存储中间节点
                cur = cur.right;  // 继续访问右子树
            }
        }
        return result;
    }
}

145. 二叉树的后序遍历

思路：左右中（出栈顺序），反过来就是中右左（出栈顺序），那么入栈顺序就是中左右。

技巧：将中右左的出栈结果反过来就是左右中（后序遍历）的结果

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<TreeNode> stack = new ArrayDeque<>();

        // 必须判断root是否为null，否则压入栈会报错，栈的元素必须为TreeNode类型
        if (root == null) return result;

        TreeNode cur = root;
        stack.push(cur);
        // 入栈：中左右    出栈：中右左
        while (!stack.isEmpty()){
            cur = stack.pop();
            result.add(cur.val);  // 中
            if (cur.left != null) stack.push(cur.left);  // 左
            if (cur.right != null) stack.push(cur.right);  // 右
        }
        Collections.reverse(result);  // 中右左 -> 左右中
        return result;
    }
}

【统一迭代】

使用原因：迭代法中前序遍历（中左右）和后序遍历（左右中）有相似之处，比较容易实现，但是中序遍历（左中右）还需要引入指针进行元素访问，复杂度较高。通过统一迭代的方式，可以将三种遍历方式的遍历方法进行统一。

主要思路：按指定遍历方式的反向将元素入栈，null只标记cur节点

144. 二叉树的前序遍历

方法一  学完中序的统一迭代后，自己写的（进步很大拉！），但思路有点不太一样。

思路：null标记的是要继续遍历的节点

1、要把root节点当作要继续遍历的节点，后面压入null，作为stack的初始情况。

2、while循环

  • cur为null时，弹出要继续遍历的节点，再按照【right -> left -> null -> cur】的方式入栈。
  • cur不为null时，将当前节点存入数组。
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();

        if (root == null) return result;
        TreeNode cur = root;
        stack.push(cur);
        stack.push(null);
        while (!stack.isEmpty()){
            cur = stack.pop();
            if (cur == null){
                if (!stack.isEmpty()){
                    cur = stack.pop();
                    if (cur.right != null) stack.push(cur.right);
                    if (cur.left != null) stack.push(cur.left);
                    stack.push(null);
                    stack.push(cur);
                }
                else{
                    break;
                }

            }
            else{
                result.add(cur.val);

            }
        }
        return result;
    }
}

方法二  按照统一迭代思路（更简单）

思路：null标记的是要存入数组的元素

  • cur不为null，按照【right -> left -> cur -> null】的顺序入栈
  • cur为null时，弹出栈顶元素，将元素存入数组
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();

        if (root == null) return result;
        TreeNode cur = root;
        stack.push(cur);

        while(!stack.isEmpty()){
            cur = stack.pop();
            if (cur != null){
                if (cur.right != null) stack.push(cur.right);
                if (cur.left != null) stack.push(cur.left);
                stack.push(cur);
                stack.push(null);
            }
            else{
                cur = stack.pop();
                result.add(cur.val);
            }
        }
        return result;
    }
}

94. 二叉树的中序遍历

思路：

  • cur不为null时，按照【right -> cur -> null -> left】的顺序入栈
  • cur为null时，弹出栈顶元素，将元素存入数组
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        if (root == null) return result;
        TreeNode cur = root;
        stack.push(cur);
        while (!stack.isEmpty()){
            cur = stack.pop();
            // cur不为null时，遍历以cur为中间节点的子树（right, cur, null, left）
            // 关键:让入栈顺序（右中左）=存入数组数据顺序（左中右）的反方向
            if (cur != null){
                if (cur.right != null) stack.push(cur.right);  // 右
                stack.push(cur);  // 中
                stack.push(null); // 此处放null是因为处理完左节点后，应该处理中节点
                if (cur.left != null) stack.push(cur.left);  // 左
            }
            // cur为null时，证明下一个弹出的元素就是该存入数组的元素
            else{
                cur = stack.pop();
                result.add(cur.val);
            }
        }
        return result;
    }
}

145. 二叉树的后序遍历

思路：

  • cur不为null时，按照【cur -> null -> right -> left】的顺序入栈
  • cur为null时，弹出栈顶元素，将元素存入数组
/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        if (root == null) return result;
        TreeNode cur = root;
        stack.push(cur);

        while(!stack.isEmpty()){
            cur = stack.pop();
            if (cur != null){
                stack.push(cur);
                stack.push(null);
                if (cur.right != null) stack.push(cur.right);
                if (cur.left != null) stack.push(cur.left);
            }
            else{
                cur = stack.pop();
                result.add(cur.val);
            }
        }
        return result;
    }
}

【现象：三种遍历方式只在cur!=null的if分支内代码不同】

前序

中序

后序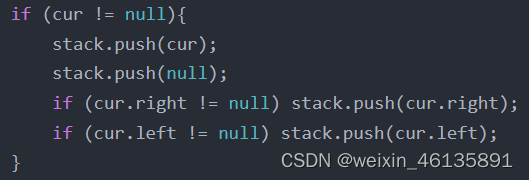

总结：

1、ArrayDeque不支持存入null元素，但LinkedList支持存入null元素。此处要存入null元素，因此只能用LinkedList。

2、统一迭代法在访问节点时，入栈顺序和指定遍历顺序相反

  • 前序遍历（中-左-右）：入栈顺序 = cur.right -> cur.left -> cur -> null（右-左-中）
  • 中序遍历（左-中-右）：入栈顺序 = cur.right -> cur -> null -> cur.left（右-中-左）
  • 后续遍历（左-右-中）：入栈顺序 = cur -> null -> cur.right -> cur.left（中-右-左）

注意：null只标记cur节点

评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值