机器学习笔记-16

无监督学习

监督学习的训练样本可能会是{$(x^{(1)},y^{(1)})、(x^{(2)},y^{(2)})...(x^{(i)},y^{(i)})$}。但是无监督学习的训练样本是{$x^{(1)}、x^{(2)}...x^{(i)}$}，没有$y$的存在。

在无监督学习的过程中我们要做的就是将这些没有标签的数据输入到算法中，让算法找到一些隐含在数据中的结构。

1.聚类算法(clustering algorithm)
聚类学算法是一个无监督学习算法，要学习不带标签的数据而不是之前带标签的数据，聚类算法将一些无标签的数据自动分类成有紧密关系的子集或者簇。K均值(K-Means)算法是现在最热门、最为广泛应用的聚类算法。

2.K-Means

K-Means算法是一个迭代算法，主要会做两件事情：簇分配和移动聚类中心(Cluster Centroids)。K-Means算法每次内循环的第一步是进行簇分配，也就是遍历每个样本，将样本根据与哪个聚类中心更近就分给哪个聚类中心（几个聚类中心就分几类）的原则进行分类。随后是移动聚类中心，

假设有一组样本如下图，要对其使用K-Means算法将其分成两类。

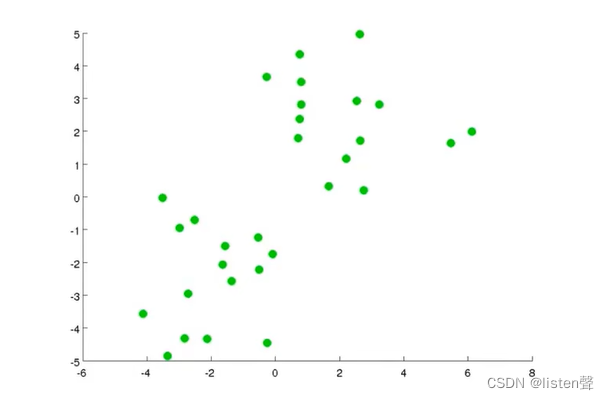
step1:随机生成两点，这两点就叫聚类中心。

选取两点的原因是因为想将数据分成两类。

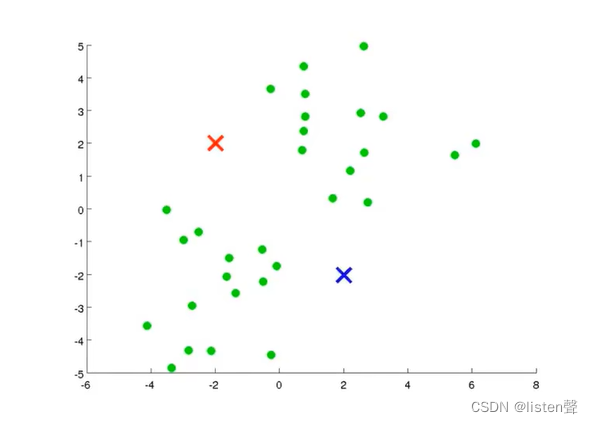
step2:进行簇分配：遍历所有样本（图上的绿点），看他们与哪个聚类中心（红叉和蓝叉）距离更近。如果与红色聚类中心更近，就分配给红叉；如果与蓝色聚类中心更近就分配给蓝叉。
通俗来讲就是遍历数据集将绿点染色染成蓝色和红色。

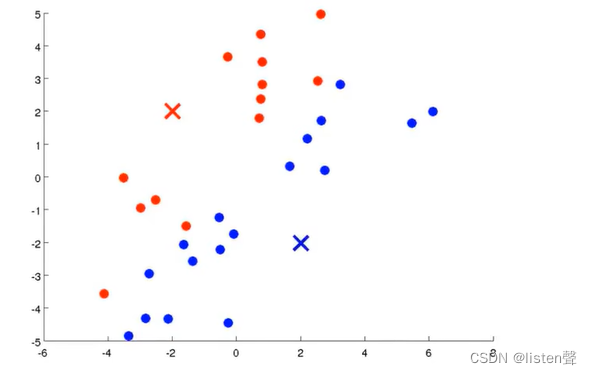
step3:移动聚类中心：找出所有红色的点算出均值，找出所有蓝色的点算出均值，然后将红叉和蓝叉移动到和他们同色的点的均值处。

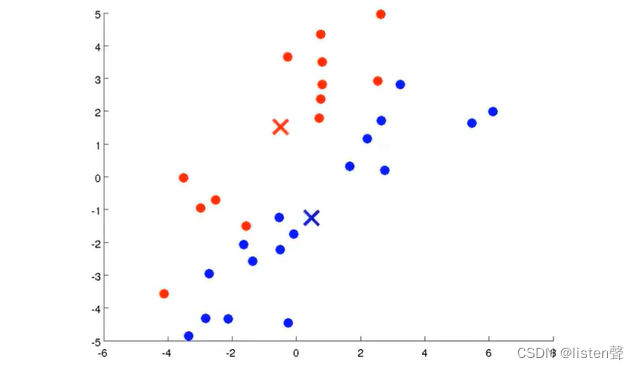
重复step2和step3，直到聚类中心不再需要移动，算法结束。

标准定义：

输入K(要分几类)和训练集。

第一个for循环在进行簇分配，随机初始化K个聚类中心${\mu }_K，c^{(i)}$是将训练样本分类后的类别序号；
第二个for循环在移动聚类中心，求出均值移动聚类中心。

比如$x^{(3)}$被划分为第五个簇，那么$c^{(3)}=5$，${\mu }_{c^{(3)}}={\mu }_5$表示第五个簇的聚类中心。

如果到最后有一个没有点的聚类中心，可以扔掉或者重新随机初始化一个。

K-Means算法的优化目标：

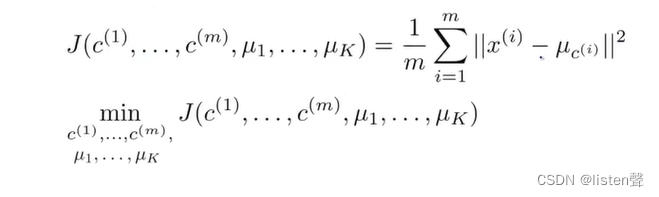
也叫失真代价函数或K-Means算法的失真。求所有样本与其所在类的聚类中心的最小值。
实际上进行簇分配和移动聚类中心的过程也就是在最小化失真函数的过程。

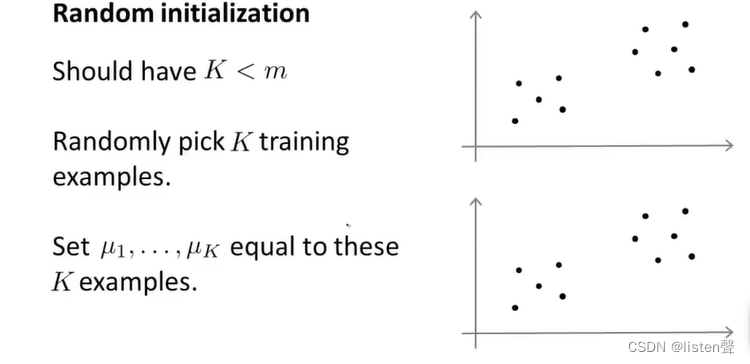
3.K-Means算法的随机初始化

聚类中心数量K应该小于样本数量m，随机选择K个样本的位置做聚类中心的位置。

K-Means算法的收敛结果随着随机初始化结果的变化而变化，可能会出现局部最优的情况。

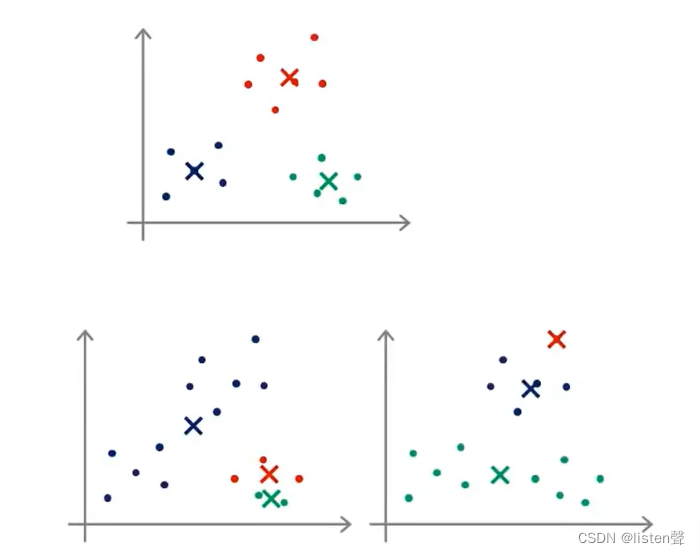
第一个图是全局最优，第二个和第三个就是局部最优，可以直观的看出并么有很好的分类。

为了避免局部最优的情况出现我们可以进行多次随机初始化，多次运行K-Means算法，具体如下：

执行100次后会得到100组数据，选择最小的

当K非常大的时候这种多次随机初始化的方法通常不会有特别大的改善，但是会有一些改善可以帮助找到合理的初始聚类中心。
对于K比较小的情况下这种方法可以帮助找到全局最优。

4.如何选择K的值

法一：
肘部法则(Elbow Method)：通过改变聚类数量计算代价函数。

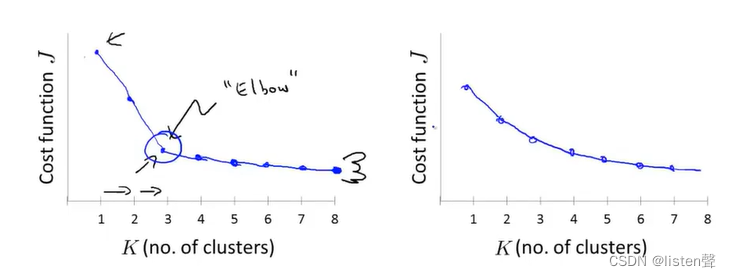
如果得到的是图1这种有清楚的拐点的图像，那么我们可以直接选择3作为聚类数量K的值；但是如果得到的是图2，肘部法则不生效。

法二：
视实际情况而定：通常我们使用聚类算法是为了分完类后用做一些用途，这时我们可以根据要做什么选取K值。