动态规划---最长公共子序列和最长公共子串

说到动态规划，不得不说到经典的最长公共子序列（Longest Common Sequence）问题和最长公共子串（Longest Common Substring），都被称为LCS问题
其中最长公共子串是最长公共子序列的衍生问题，我们今天来重点讨论一下这两个问题。
首先我们先区分一下最长公共子序列和最长公共子串，直接举一个例子就能明白。比如给你两个字符串分别数adminos和admins,请问它们的最长公共子序列和最长公共子串分别是什么嘞？
最长公共子序列：admins
最长公共子串：admin
通过比较，我们发现最长公共子序列是不考虑字符之间是否是连续的，中间就算隔了好几个其他字符，只要存在公共字符，就算在公共子序列里面。反之，最长公共子串因为要求的是一个字符串，所谓公共字符串那么所有的公共字符都必须是连续出现的。所以，上题中adminos和admins，‘a’,‘d’,‘m’,‘i’,‘n’,'s’都是公共字符，按照要求我们要达到最长的子序列和最长的子串，则尽量使他们都出现，所以admin是我们的最长公共子串，admins是我们最长公共子序列。
弄懂了这个， 我们就可以把这两个问题，搬到我们程序中去了。
我们重点论述最长公共子序列，由于示意图手画出来不好看，我找了几张清晰的图片来替代

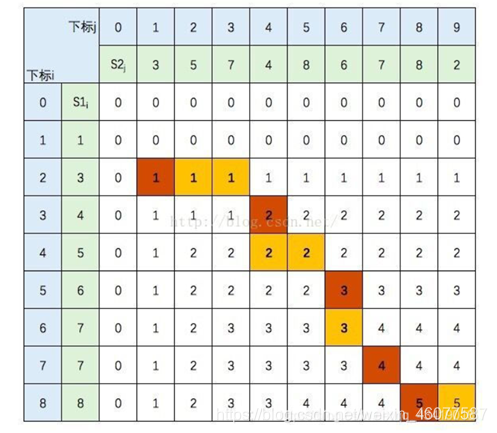
对于动态规划问题，要想写出程序，我们要弄懂写出它的状态转移方程。我们来分析这张图，这张图比较的是“1 3 4 5 6 7 7 8”和“3 5 7 4 8 6 7 8 2”这两个字符串，根据我们前面所讲的，我们凭肉眼可以判断它们的最长公共子序列为3 4 6 7 8，长度为5。
再来看我们的程序应该怎样做才能算出来嘞？
我们可以从下标1开始把两个字符串存储在两个字符串数组a和b中,再初始化一个二维数组dp[maxn][maxn]，我们最后的最长公共子序列的长度就存储在里面。然后逐一比较a数组和b数组中字符是否相等（当然是放在一个双重for循环中)。对于比较情况有两种情况：
1.a[i] == b[j],则最长公共子序列增加1位，就有dp[i][j] = dp[i-1][j-1]+1(因为有i-1和j-1,这就是为什么我们要从下标1开始存储字符串)

如上图，a[2] == b[1] ==3, 那么在二维数组dp中，dp[2][1] = dp[2-1][1-1] = dp[1][0] + 1 (dp[1][0]==0) = 1
2.当a[i]!=b[j]时，则我们的最长公共子序列长度不能再加1，但我们要把我们之前比较的成果，也就是当下最长公共子序列的长度保存下来，如果不这样做的话，那么最后得到的长度肯定不是最长的。我们不妨这样想，dp中那些字符不相等的空间，反正闲着也是闲着不如帮我们把子序列的长度保存下来，就像这样

深橘黄色的部分代表我们相等的字符，而黄色的部分就是字符不相等的空间，我们把它们用来存储当下的最长公共子序列的长度1。可以看到，到下一对相等的字符，正好有一个字符不相等的空间位于其斜上方，然后再加1，我们就成功实现了最长公共子序列长度的传递。但想到这儿还不够，我们的最终目的是要得到最长的公共子序列，我们要尽可能地让我们子序列的长度最大，对于存储的最长公共子序列的长度，我们如何要让它最长，那就可以比较相邻上方和相邻左方（因为我们整个dp是往右下方比较的，所以只需比较相邻上方和相邻左方这两个方向），哪个最大我们就存哪个。如图

分析到这个我们就可以得到我们它的状态转移方程了

还需要的注意的是，我们初始化一个二维dp[i][j]数组时,由于字符串是从下标1开始的，那么我们要把dp[i][0]和dp[0][j]都赋值为0，这样保证最大公共子序列的长度从0开始的。
完整代码：

#include<bits/stdc++.h>
using namespace std;
const int maxn = 20;
int dp[maxn][maxn