机器学习回归与聚类算法

线性回归

        回归问题：

                目标值  -  连续型的数据

线性回归的原理

        什么是线性回归

             函数关系   特征值和目标值

        广义线性模型

                线性关系：自变量为一次

                非线性关系

                线性模型

                        自变量一次

                                y = w1x1   +   w2x2  +  w3x3  +   ...  + wnxn    +  b

                          参数一次(参数就是w1，w2...)

                                y = w1x1 + w2x1^2 + w3x1^ 3  +  ... + b 

                线性关系一定是线性模型，但是线性模型不一定是线性关系

        线性回归的损失和优化原理

                目标：求模型参数

                         模型参数能够使得预测准确

                损失函数

                           又名最小二乘法

                优化损失

                        优化方法（去求模型中的参数 ，使得损失最小）（找到最小损失对应的参数）

                                1.正规方程

                                        直接求解w

                                2.梯度下降         

                                        试错、改进

        线性回归API

        回归性能评估

        

        正规方程和梯度下降对比

                

        

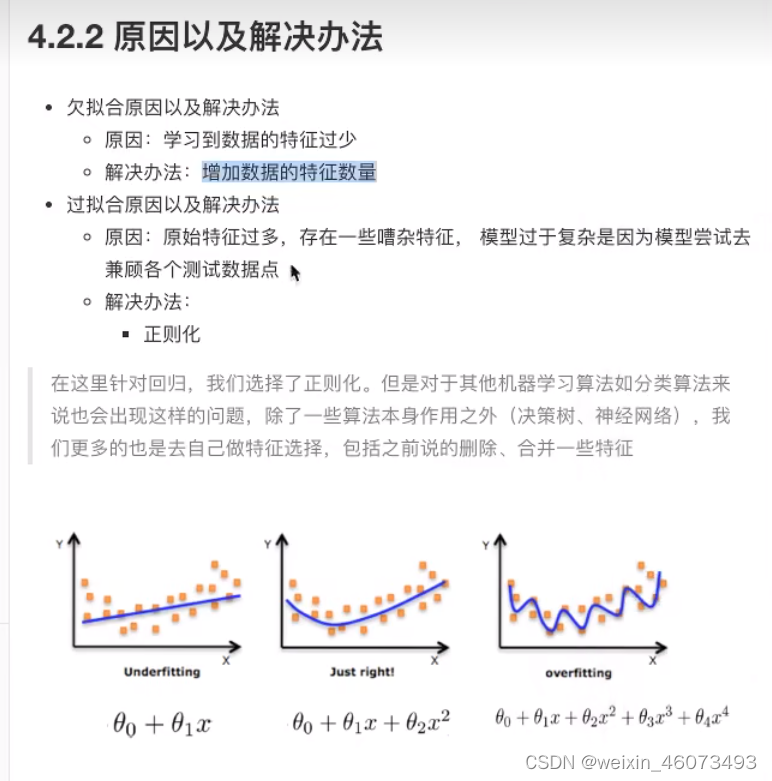
  过拟合与欠拟合

                                在训练集上表现的很好，但是在测试集上表现不好 -- 过拟合

                        原因与解决方法

                        

分类算法-逻辑回归与二分类

        逻辑 回归的应用场景

                广告点击率         是否会被点击

                金融诈骗             是否为金融诈骗

                虚假账号              是否为虚假账号

                正例 / 反例

        逻辑回归的原理

                

        逻辑回归的输入就是线性回归的输出

        怎么进行分类

                        将线性回归的输出代入到 激活函数中 （可以得到0到1区间的数[可以理解为概率值] 设置一个阈值，如果大于该阈值就认为属于该类别，如果小于这个阈值就认为不属于该类别）

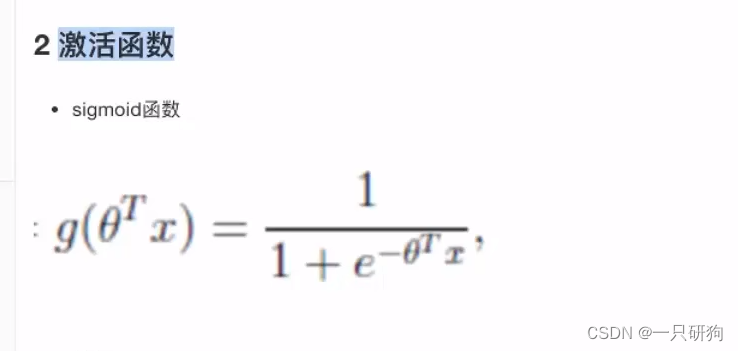
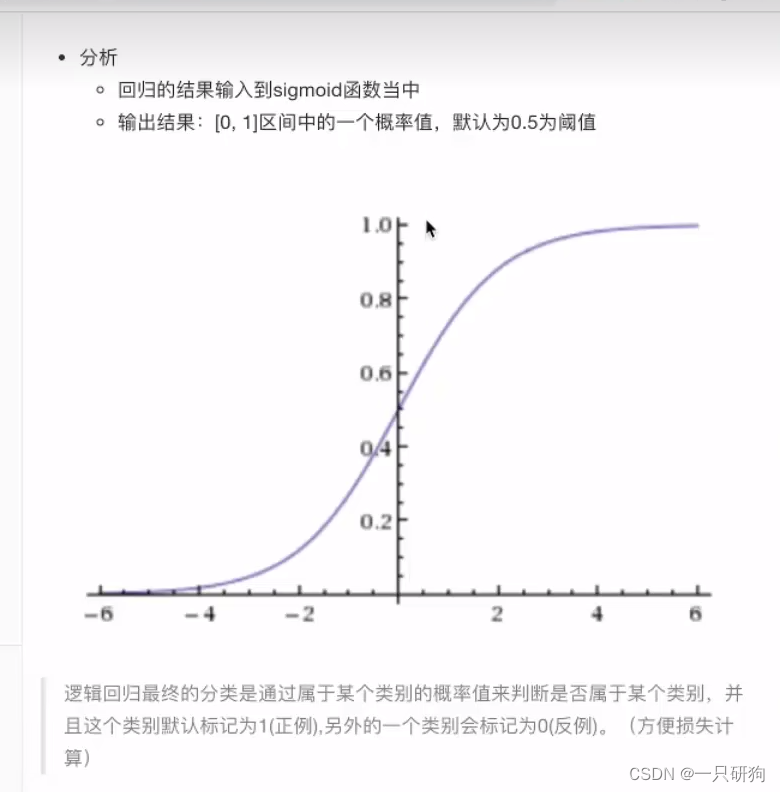        如果大于0.5就属于该类别，如果小于0.5就不属于该类别

                如何得出一组权重和偏置使得该模型可以进行准确的分类预测

                

                构建一个损失函数，用一种优化方法使得损失函数取得最小值，此时会得到一组权重和偏置，这种权重和偏置就是要求的权重和偏置。

           损失以及优化

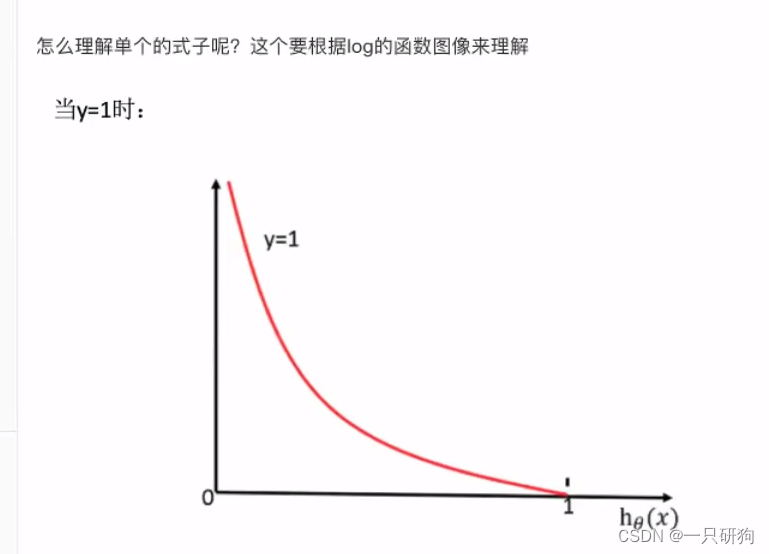
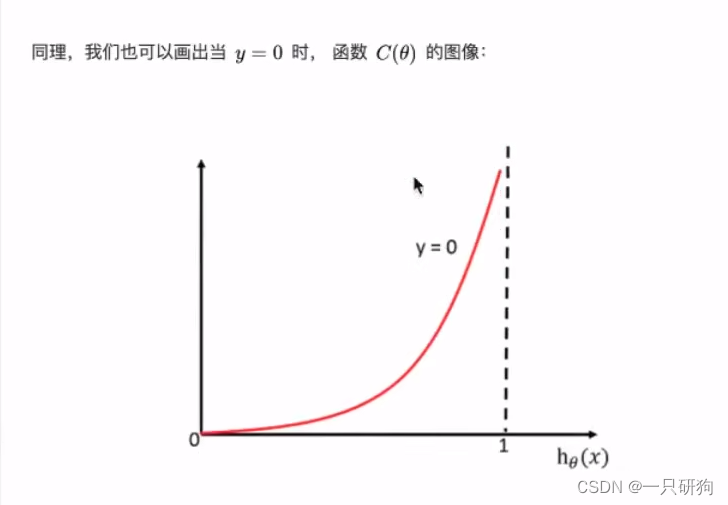
                如何确定该损失函数

                 使用(y_predict - y_true)/总数

                逻辑回归的真实值/预测值   是否属于某个类别  所以无法使用均方误差

       

        分类的评估方法

                         精确率与召回率

       

                精确率：预测结果为正例样本中的真实为正例的比例

                召回率：真实为正例的样本中预测结果正例的比例

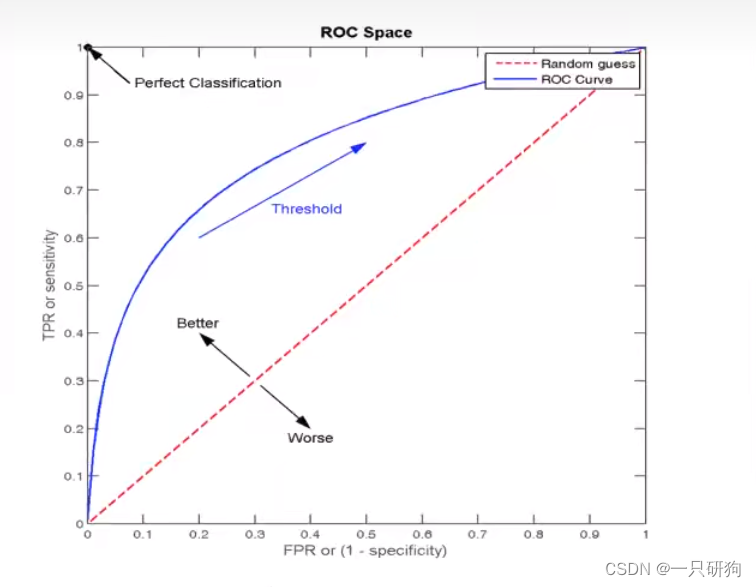
                        ROC曲线与AUC指标

                                        防止样本不均衡

                                        例如：总共100个人，如果有99个样本癌症，1个样本非癌症 -- 样本不均衡

                AUC只能用来评价二分类

                AUC非常适合评价样本不平衡中的分类器性能

无监督学习包含算法

        聚类----K-means（K均值聚类）

        降维 --- PCA

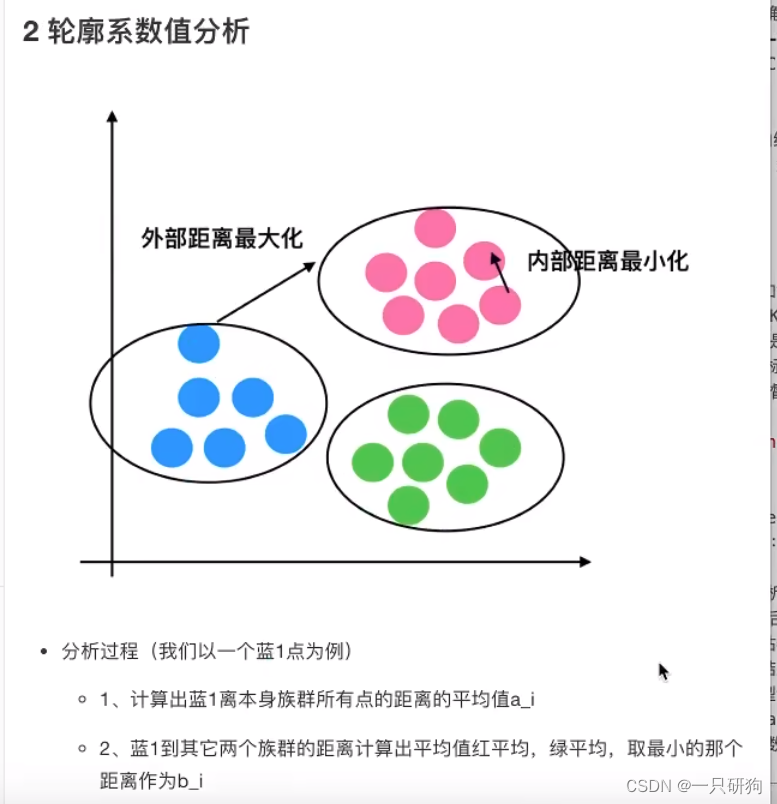
        KMeans性能评估指标

                轮廓系数