高精度加法

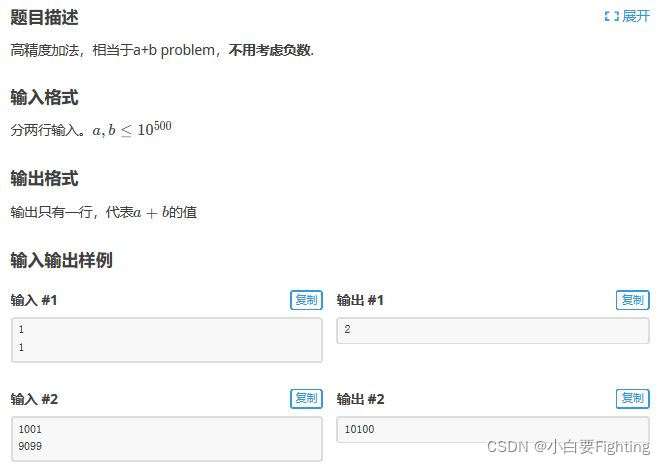
用数组存储数据，以下题为例：

A+B Problem（高精） - 洛谷

算法描述可参考：（可以在草稿本上依据该描述模拟两个数相加的过程来理解其思想）

 

思路：

①读取字符串，并将字符串转为整数数组，个位在整数数组第0位，以947+34为例

整数数组A：

7

4

9

整数数组B：

4

3

#include <bits/stdc++.h>

using namespace std;

int A[100000], B[100000], C[10000000];
//以947 + 34 为例：
int main(){
    string a,b;
    cin >> a; //以字符串存储加数 a
    cin >> b;  //以字符串存储被加数 b
    int lena = a.size(); //获取a的长度
    int lenb = b.size(); //获取b的长度
    int k = lena - 1;
    int m = lenb - 1;
    //将a转换为整数数组A，个位即A[0]
    // 9 4 7----->  A[0] = 7 = a[2]        A[1] = 4 = a[1]    A[2] = 9 = a[0]
    //A的下标以a下标的关系: A的下标 = a字符串的长度 - 1 - a的下标
    for(int i = lena-1; i >= 0; i--){
        A[k-i] = a[i] - '0';  
    }
    //将b转换为整数数组B，个位即B[0]
    for(int i = lenb - 1; i >= 0; i--){
        B[m-i] = b[i] - '0';
    }
    // 输出A， B进行验证
   /* for(int i = 0; i < lena; i++){
        cout << A[i] << " ";
    }
    cout << endl;
    for(int i = 0; i < lenb; i++){
        cout << B[i] << " ";
    }*/

② 令temp = 0，x 表示两个数对应为相加再加上进位的和，x = A[i] + B[i] + temp；

如果x >= 10, 即x 为两位数， 整数数组C表示和，C的对应位为 x % 10, temp = 1;

    int temp = 0; //表示进位
    int c = lena >= lenb ? lena : lenb; //获取a，b两者的最大长度
    //得到C数组
    for(int i = 0; i < c; i++){
        int x = A[i] + B[i] + temp; 
        C[i] = x % 10; 
        temp = x / 10;
    }

以947 + 34为例：

i = 0 : A[0] = 7, B[0] = 4, x = 7 + 4 + 0 = 11, C[0] = 1, temp = 1;

i = 1 : A[1] = 4, B[1] = 3, x = 4 + 3 + 1 = 8, C[0] = 8, temp = 0;

i = 2 : A[2] = 9, B[2] = 0, x = 9 + 0 + 0 = 9, C[0] = 9, temp = 0;

③ 输出结果

如果temp = 0，直接输出C数组

如果temp = 1，C[c] = 1, 再输出C数组

    if(temp == 0){
        for(int i = c-1; i >= 0; i--){
            cout << C[i];
        }
    }
    if(temp == 1){
        C[c] = temp;
        for(int i = c; i >= 0; i--){
            cout << C[i];
        }
    }

总的代码：

#include <bits/stdc++.h>

using namespace std;

int A[100000], B[100000], C[10000000];

int main(){
    string a,b;
    cin >> a;
    cin >> b;
    int lena = a.size();
    int lenb = b.size();
    int k = lena - 1;
    int m = lenb - 1;
    for(int i = lena-1; i >= 0; i--){
        A[k-i] = a[i] - '0';
    }
    for(int i = lenb - 1; i >= 0; i--){
        B[m-i] = b[i] - '0';
    }
   /* for(int i = 0; i < lena; i++){
        cout << A[i] << " ";
    }
    cout << endl;
    for(int i = 0; i < lenb; i++){
        cout << B[i] << " ";
    }*/
    int temp = 0;
    int c = lena >= lenb ? lena : lenb;
    for(int i = 0; i < c; i++){
        int x = A[i] + B[i] + temp;
        C[i] = x % 10;
        temp = x / 10;
    }
    if(temp == 0){
        for(int i = c-1; i >= 0; i--){
            cout << C[i];
        }
    }
    if(temp == 1){
        C[c] = temp;
        for(int i = c; i >= 0; i--){
            cout << C[i];
        }
    }
    return 0;
    
}