数据结构——二叉树

一、满二叉树

1. 定义： 在一棵二叉树中，如果所有分支结点都存在左子树和右子树，并且所有叶子都在同一层。
2. 特点： 叶子只能出现在最下一层；只有度为0和度为2的结点。

二、完全二叉树

1. 定义： 对一棵具有n个结点的二叉树按层序编号，如果编号为i（1<= i <=n）的结点与同样深度的满二叉树中编号为i的结点在二叉树中的位置完全相同。
2. 满二叉树，是特殊的完全二叉树。

三、二叉树的基本性质

• 如果叶子结点的个数为n₀，度为2的结点个数为n₂，则n₀=n₂+1。
• 二叉树的第i层上最多有 2^i-1 结点（i>=1)。
• 在一棵深度为k的二叉树中，最多有2^k-1个结点。
• 具有n个结点的完全二叉树的深度为[log₂n]+1。（[ ]符号表示“下取整”）
• 对一棵具有n个结点的完全二叉树从1开始按层序编号，则对于编号为i（1<= i <= n)的结点（简称为结点i），有如下关系成立：
  1）如果i>1,则结点 i 的双亲的编号为 [i/2] ；否则结点 i 是根节点，无双亲。
  2）如果2i <= n,则结点 i 的左孩子的编号为2i;否则结点 i 无左孩子。
  3）如果2i+1 <= n,则结点 i 的右孩子的编号为2i+1;否则结点 i 无右孩子。

四、二叉树的遍历操作

1. 前序遍历（前根遍历）：

• 访问根结点；
• 前序遍历根结点的左子树；
• 前序遍根结点的右子树。
• eg : 求下图前序遍历的顺序？

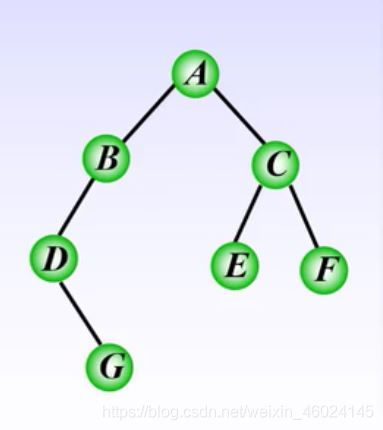
前序遍历的序列为：A-B-D-G-C-E-F

2. 中序遍历（中根遍历）：

• 中序遍历根结点的左子树；
• 访问根结点；
• 中序遍根结点的右子树。
• eg : 求下图中序遍历的顺序？

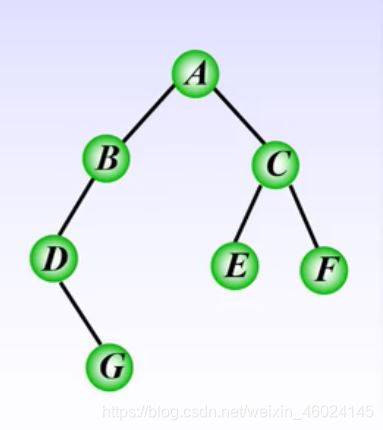
中序遍历的序列为：D-G-B-A-E-C-F

3. 后序遍历（后根遍历）：

• 后序遍历根结点的左子树；
• 后序遍根结点的右子树；
• 访问根结点。
• eg : 求下图后序遍历的顺序？

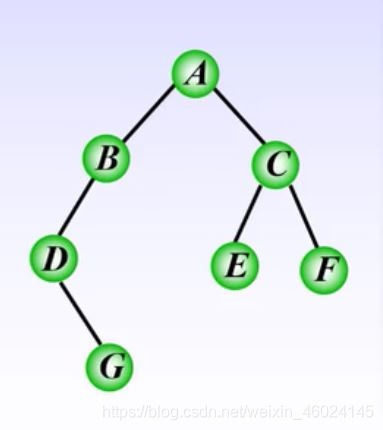
后序遍历的序列为：G-D-B-E-F-C-A

五、二叉树性质的习题解析

1. 一棵二叉树的第i （i>=1）层最多有（ ）个结点？

当二叉树为满二叉树时，第i层的结点最多，因此，答案为：2^i-1

2. 一棵有n（n>0)个结点的满二叉树共有（ ）个叶子结点 和 （ ）个非叶子结点。

根据满二叉树推算得出，“叶子节点”总是比“非叶子结点”多一个，因此 :
叶子结点的个数为：（n+1）/2 ;
非叶子结点的个数为：（n-1）/2

3. 具有100个结点的完全二叉树的“叶子结点”数为（ ）。

完全二叉树结点为100，是个偶数，可以推出缺了一个叶子结点，又根据满二叉树叶子结点总是比非叶子结点多一个，由此推出：该题中叶子结点 = 非叶子结点，因此，答案为：50

4. 深度为k的完全二叉树至少有（ ）个结点，至多有（ ）个结点。

深度为k的完全二叉树，结点最少（说明最后一层只有一个叶子，即 k-1 层的满二叉树加一个结点），k-1 层的满二叉树的结点数为 2^k-1-1, k 层的满二叉树的结点数为 2^k-1, 因此：
深度为k的完全二叉树，至少有2^k-1-1+1（k-1 层的满二叉树加一）
深度为k的完全二叉树，至多有2^k-1（k 层为满二叉树）

5. 具有n个结点的完全二叉树按层序从1开始编号，则编号最小的叶子的序号是（）。

完全二叉树，如果一个结点有左孩子和右孩子，则左孩子是该结点的两倍，右孩子是该结点的两倍加一。最小的叶子结点，就是最后一个叶子结点n的双亲结点n/2加一，因此，答案为：[n/2]+1

6. 某二叉树的前序遍历序列是ABCDEFG，中序遍历序列是CBDAFGE,则其后续遍历序列是（ ）。

第一步：找出根结点

• 前序遍历序列是ABCDEFG (根据前序序列可以判断出A为根结点)
• 中序遍历序列是CBDAFGE（A的左边CBD为左子树，A的右边FGE为右子树）
  
  
  第二步：确定A左子树
• 前序遍历序列是ABCDEFG (根据前序序列可以判断出B为左子树的根结点)
• 中序遍历序列是CBDAFGE（B的左边C为左子树，B的右边D为右子树）
  
  
  第三步：确定A右子树
• 前序遍历序列是ABCDEFG (根据前序序列可以判断出E为右子树的根结点)
• 中序遍历序列是CBDAFGE（E的左边FG为左子树，E的右边为空，代表E没有右子树）
  
  
  第四步：确定A右子树中，E的左子树
• 前序遍历序列是ABCDEFG (根据前序序列可以判断出F为E左子树下面的根结点)
• 中序遍历序列是CBDAFGE（F的左边为空，代表F没有左子树，F的右边G为右子树）
  
  
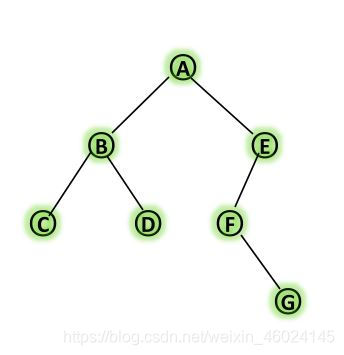
  第五步：画出二叉树
  
  
  
  第六步：根据二叉树图，写出该二叉树的后续遍历序列：C-D-B-G-F-E-A