逻辑斯蒂回归

最新推荐文章于 2024-12-19 05:00:00 发布

原创最新推荐文章于 2024-12-19 05:00:00 发布

· 142 阅读

1 ·

版权

数据分析和机器学习专栏收录该内容

21 篇文章

订阅专栏

knn 是一个非解析得方法（地推）
我们期望找到一个回归问题得解析解

在这里插入图片描述

假如我们有两坨可分得数据
我们可以在他们之间画一条直线y=x,如果x>y 就是1类，x<y 就是2类
这根线叫向量超平面
离这个线多远算好，多近算好

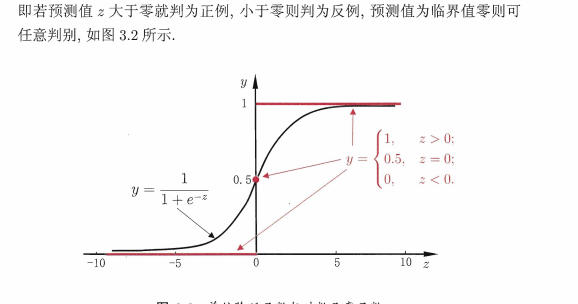
在这里插入图片描述

于是把他映射到0-1区间，如果1就认为你特别好，0也特别好，中间就不是很好

逻辑斯蒂函数

把我们没有标准的一个距离分界面映射到0-1的概率区间可以判断
0，和1都是百分百

解析方法模型

在这里插入图片描述

最大自然估计损失函数

用样本值估计参数

#条件概率公式

后叶概率 (一般无法直接计算)      通过先叶概率进行推断(你见过的进行推断)
							似然函数
P = (性别=?|学计算机)		=	(学计算机|性别=男)*p(性别=男)

贝叶斯公式
我们要计算P(A|B)

#联合概率
P(AB) = P(A|B)P(B) = P(B|A)P(A)

没办法直接算
P(A|B) ！！可能性函数

				P(AB)			p(B|A)P(A)
	P(A|B) = ———————————— 	= ————————————
				P(B)			P(B)


P(小偷?|鬼鬼祟祟) = P(鬼鬼祟祟|小偷) * P(小偷)

在这里插入图片描述

x，y 为我们看到得值
θ

在这里插入图片描述

混淆矩阵

横项是真实数据纵项是正实数据
交叉验证
横项代表召回率
纵向代表精确度

在这里插入图片描述

在这里插入图片描述
一共30 条数据

				 预测结果
				一		二		三	
		   一	[14		0		0]  
			
真实结果	   二	[0		9		1]
			
		   三	[0		0		6]

第一类鸢尾花实际有14朵   预测结果也是14朵正确率100

第二类鸢尾花有10朵    预测了9朵是第二类，有一朵第二类被预测成第三类 正确率90

第三类鸢尾花有6朵 		预测了6朵是第三类

算法认为第三类花一共有1+6=7朵
实际上只有6朵 

算法精确率 = 6/7

例二

在这里插入图片描述

在医疗体系中

一台机器有几个任务
做检查机器是经可能提高召回率还是尽可能提高精确度

召回率代表经可能把有病得都找出来

精确度代表有病就判有病

  实验条件  1000 样本
  机器认为 100 个人有病   ——》99真有病 精确度百分之99
  潜在有病200 人     			——》 漏判101人  召回率不搞

算法精确率 = 120 / 1648

召回率（查全率)  =   120/147

例子三

from sklearn.datasets import load_iris,load_digits

from sklearn.model_selection import train_test_split


li = load_digits()


train_data,test_data   ,train_target,test_target    =    train_test_split(li.data,li.target,test_size=0.2)



# 逻辑斯蒂回归
from sklearn.linear_model import LogisticRegression
            #逻辑回归得混淆矩阵
from sklearn.metrics import confusion_matrix

# 有一个参数C  正则化强度得倒数
# 越大正则化强度越弱   太小和瞎猜一样
# 越小正则化强度越强    太大容易学到噪声  默认1.0


lr_class = LogisticRegression(C=1.0)
lr_class.fit(train_data,train_target)

# 混淆矩阵会自动帮我们对比真实值和预测值得结果  不同得找出来
print(confusion_matrix(test_target,lr_class.predict(test_data)))