L2-013 红色警报 (25分)【并查集】

题目描述
战争中保持各个城市间的连通性非常重要。本题要求你编写一个报警程序，当失去一个城市导致国家被分裂为多个无法连通的区域时，就发出红色警报。注意：若该国本来就不完全连通，是分裂的k个区域，而失去一个城市并不改变其他城市之间的连通性，则不要发出警报。

输入格式：
输入在第一行给出两个整数N（0 < N ≤ 500）和M（≤ 5000），分别为城市个数（于是默认城市从0到N-1编号）和连接两城市的通路条数。随后M行，每行给出一条通路所连接的两个城市的编号，其间以1个空格分隔。在城市信息之后给出被攻占的信息，即一个正整数K和随后的K个被攻占的城市的编号。

注意：输入保证给出的被攻占的城市编号都是合法的且无重复，但并不保证给出的通路没有重复。

输出格式：
对每个被攻占的城市，如果它会改变整个国家的连通性，则输出Red Alert: City k is lost!，其中k是该城市的编号；否则只输出City k is lost.即可。如果该国失去了最后一个城市，则增加一行输出Game Over.。

输入样例：

5 4
0 1
1 3
3 0
0 4
5
1 2 0 4 3

输出样例：

City 1 is lost.
City 2 is lost.
Red Alert: City 0 is lost!
City 4 is lost.
City 3 is lost.
Game Over.

这又是一道并查集的题，关键是去计算每次操作之后的连通分量个数。因为他是去除节点，所以我的初始思路是直接从并查集中删除该节点，但发现实际操作起来很困难，与该节点相关的节点不知道怎么去处理。于是就去上网搜题解，发现别人的思路是每次操作之后都重新再初始化建立一个新的并查集，并计算连通分量进行比较。

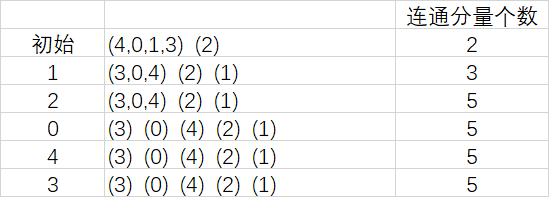
这里需要注意的是连通分量如何进行比较，格外需要强调的是，攻破一个城市之后，并不是删除该城市，而是将它单独划分出来为一个连通分量。 设原连通分量个数为cnt，新连通分量个数为cnt2；如果cnt == cnt2，说明连通性未改变，直接输出City k is lost.；如果cnt2 - cnt == 1，表明被攻占的城市是一个外围城市，删除它之后，它本身独立出来增加一个连通分量，其余城市连通性不改变，故也是输出City k is lost.；只有当cnt2 - cnt > 1的时候，才改变其他城市连通分量，输出Red Alert: City k is lost!

#include <iostream>
using namespace std;
int fa[505];
void init() {      //初始化
	for(int i = 0; i < 505; i++) {
		fa[i] = i;
	}
}
int find(int x) {     //寻找根节点
	if(fa[x] == x) return x;
	return fa[x] = find(fa[x]);
}
void merge(int x, int y) {    //合并
	int fx = find(x), fy = find(y);
	if(fx != fy) fa[fx] = fy;
}
int count(int x) {    //计算连通分量
	int cnt = 0;
	for(int i = 0; i < x; i++) {
		if(fa[i] == i) cnt++;
	}
	return cnt;
}
struct node{
	int a, b;
};
int main() {
	int n, m;
	cin >> n >> m;
	init();
	node node[m];
	for(int i = 0; i < m; i++) {
		cin >> node[i].a >> node[i].b;
		merge(node[i].a, node[i].b);
	}
	int cnt = count(n);
	int vis[n] = {0};
	int k;
	cin >> k;
	for(int i = 0; i < k; i++) {
		int t;
		cin >> t;
		vis[t] = 1;
		init();      //初始化,重新建立并查集求连通分量
		for(int i = 0; i < m; i++) {
			if(vis[node[i].a] || vis[node[i].b]){
				continue;
			}
			else {
				merge(node[i].a, node[i].b);
			}
		}
		int cnt2 = count(n);
		if(cnt == cnt2 || cnt2 == cnt+1) printf("City %d is lost.\n", t);
		else printf("Red Alert: City %d is lost!\n", t);
		cnt = cnt2;
	}
	if(cnt == n) {
		printf("Game Over.");
	}
}