数据结构之栈和队列

一.栈和队列

1.栈

栈（Stack）：是只允许在一端进行插入或删除的线性表。首先栈是一种线性表，但限定这种线性表只能在某一端进行插入和删除操作。

栈顶：数据从栈顶进栈，也从栈顶出去；
栈底：固定的，不能做栈顶的操作；
空栈：里面没有任何元素。

栈又称为后进先出（Last In First Out）的线性表，简称LIFO结构

1.1栈的常见操作

• InitStack(&S)：初始化一个空栈S。
• StackEmpty(S)：判断一个栈是否为空，若栈为空则返回true，否则返回false。
• Push(&S, x)：进栈（栈的插入操作），若栈S未满，则将x加入使之成为新栈顶。
• Pop(&S, &x)：出栈（栈的删除操作），若栈S非空，则弹出栈顶元素，并用x返回。
• GetTop(S, &x)：读栈顶元素，若栈S非空，则用x返回栈顶元素。
• DestroyStack(&S)：栈销毁，并释放S占用的存储空间（“&”表示引用调用）。

1.2栈的存储结构

1.2.1顺序存储结构

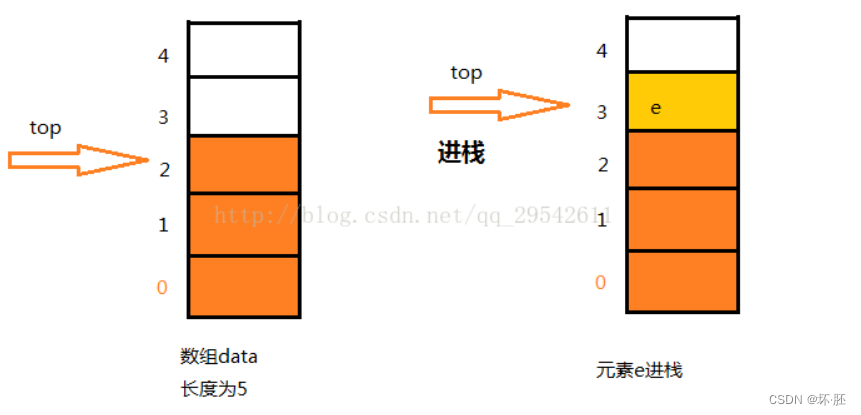
采用顺序存储的栈称为顺序栈，它利用一组地址连续的存储单元存放自栈底到栈顶的数据元素，同时附设一个指针（top）指示当前栈顶元素的位置。
若存储栈的长度为StackSize，则栈顶位置top必须小于StackSize。当栈存在一个元素时，top等于0，因此通常把空栈的判断条件定位top等于-1。
它的特殊之出在于限制了这个线性表的插入和删除位置，它始终只在栈顶进行。这使得：栈底是固定的，最先进栈的只能在栈底。
栈的插入叫 进栈也称 压栈、入栈。
栈的删除叫出栈，也称弹栈。
当然 压栈和出栈是栈最重要的算法。
实际上栈在程序中用的是特别多的，比如浏览器的前进后退，文档的撤销操作等都是用的栈的方式。

1.2.2链式存储结构

栈的链式存储结构，简称链栈。
由于栈只是栈顶在做插入和删除操作，所以栈顶应该放在单链表的头部。另外，都有了栈顶在头部了，单链表中的头结点也就失去了意义，通常对于链栈来说，是不需要头结点的。
对于链栈来说，基本不存在栈满的情况，除非内存已经没有使用空间了。
对于空栈来说，链表原来的定义是头指针指向空，那么链栈的空其实就是top＝NULL。

链栈的进栈push和出栈pop操作都很简单，时间复杂度均为O(1)。

对比一下顺序栈与链栈,它们在时间复杂度上是一样的,均为O(1)。对于空间性能,顺序栈需要事先确定一个固定的长度,可能会存在内存空间浪费的问题,但它的优势是存取时定位很方便,而链栈则要求每个元素都有指针域,这同时也增加了一些内存开销,但对于栈的长度无限制。所以它们的区别和线性表中讨论的一样,如果栈的使用过程中元素变化不可预料,有时很小,有时非常大,那么最好是用链栈,反之,如果它的变化在可控范围内,建议使用顺序栈会更好一些。

2.栈的应用——递归

递归的定义
递归是一种重要的程序设计方法。简单地说,若在一个函数、过程或数据结构的定义中又应用了它自身,则这个函数、过程或数据结构称为是递归定义的,简称递归。
它通常把一个大型的复杂问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的代码就可以描述岀解题过程所需要的多次重复计算,大大减少了程序的代码量但在通常情况下,它的效率并不是太高。

2.1后缀表达式计算结果

表达式求值是程序设计语言编译中一个最基本的问题,它的实现是栈应用的一个典型范例。中缀表达式不仅依赖运算符的优先级,而且还要处理括号。后缀表达式的运算符在操作数后面，在后缀表达式中已考虑了运算符的优先级,没有括号,只有操作数和运算符。例如中缀表达式A + B ∗ ( C − D ) − E / F A+B(C-D)-E/FA+B∗(C−D)−E/F所对应的后缀表达式为A B C D − ∗ + E F / − ABCD-*+EF/-ABCD−∗+EF/−。_

后缀表达式计算规则：从左到右遍历表达式的每个数字和符号，遇到是数字就进栈，遇到是符号，就将处于栈顶两个数字出栈，进项运算，运算结果进栈，一直到最终获得结果。

2.2中缀表达式转后缀表达式

我们把平时所用的标准四则运算表达式,即a + b − a ∗ ( ( c + d ) / e − f ) + g a+b-a*((c+d)/e-f)+ga+b−a∗((c+d)/e−f)+g叫做中缀
表达式。因为所有的运算符号都在两数字的中间,现在我们的问题就是中缀到后缀的转化。

规则:从左到右遍历中缀表达式的每个数字和符号,若是数字就输出,即成为后
缀表达式的一部分;若是符号,则判断其与栈顶符号的优先级,是右括号或优先级低于栈顶符号(乘除优先加减)则栈顶元素依次出栈并输出,并将当前符号进栈,一直到最终输出后缀表达式为止

二.队列

1.定义

它是一个操作受限的线性表，只允许在表的一端（rear，对尾）进行元素的插入，另一端（front，队头）进行元素的删除。

2.常见操作

InitQueue(&Q)：初始化队列，构造一个空队列Q。
QueueEmpty(Q)：判队列空，若队列Q为空返回true，否则返回false。 EnQueue(&Q,
x)：入队，若队列Q未满，将x加入，使之成为新的队尾。 DeQueue(&Q, &x)：出队，若队列Q非空，删除队头元素，并用x返回。
GetHead(Q, &x)：读队头元素，若队列Q非空，则将队头元素赋值给x。

3.队列的存储结构

3.1顺序存储

队列的顺序存储结构又称为顺序队列，它也是利用一块连续的存储单元放队列中的元素的，是一个受限的线性表。

初始状态（队空条件）：Q->front == Q->rear == 0。
进队操作：队不满时，先送值到队尾元素，再将队尾指针加1。
出队操作：队不空时，先取队头元素值，再将队头指针加1。

循环队列：
相较于一般队列来操作，当两个指针插入和删除记录的元素个数相差较大，会造成假溢，而循环队列，相当于一个环状数组，解决了一般数组的空间的浪费。

初始时：Q->front = Q->rear=0。
队首指针进1：Q->front = (Q->front + 1) % MAXSIZE。
队尾指针进1：Q->rear = (Q->rear + 1) % MAXSIZE。
队列长度：(Q->rear - Q->front + MAXSIZE) % MAXSIZE。

为了区分队空还是队满的情况，有三种处理方式：
（1）牺牲一个单元来区分队空和队满，入队时少用一个队列单元，这是种较为普遍的做法，约定以“队头指针在队尾指针的下一位置作为队满的标志”，如图 ( d2 ）所示。

队满条件： (Q->rear + 1)%Maxsize == Q->front
队空条件仍： Q->front == Q->rear
队列中元素的个数： (Q->rear - Q ->front + Maxsize)% Maxsize
（2）类型中增设表示元素个数的数据成员。这样，队空的条件为 Q->size == O ；队满的条件为 Q->size == Maxsize 。这两种情况都有 Q->front == Q->rear
（3）类型中增设tag 数据成员，以区分是队满还是队空。tag 等于0时，若因删除导致 Q->front == Q->rear ，则为队空；tag 等于 1 时，若因插入导致 Q ->front == Q->rear ，则为队满。

3.2链式存储

链队列
队列的链式存储结构表示为链队列，它实际上是一个同时带有队头指针和队尾指针的单链表，只不过它只能尾进头出而已。
通常用一个头指针和一个尾指针唯一确定，也通常把队列的两个指针封装在一起。

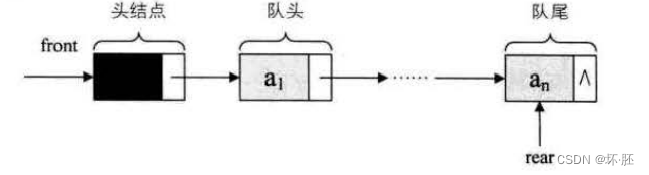
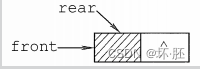
空队列时，front和real都指向头结点。

3.2.1链队列常见算法

（1）链队列存储类型
当Q->front == NULL 并且 Q->rear == NULL 时，链队列为空。

（2）链队列初始化

（3）链队列入队

（4）链队列出队

记得三连，好运连连！！！！！