【数据结构6（2）】第五章 树和二叉树 | 线索二叉树、哈夫曼树的构造、哈夫曼编码、二叉树、树、森林互相转换、树的表示（双亲表示法等四种表示方法）

用于学习

目录

第五章 树和二叉树（2）

问题1:如何可唯一地确定一棵二叉树?

问题2:二叉树的二叉树链表存储结构中，有多少个指针域未利用?

5.5  线索二叉树

问题1∶为什么二叉树中加入线索?

问题2∶如何在二叉树中加入线索?

问题3 :怎样来区分孩子指针域中存放的是左、右孩子信息还是直接前驱或直接后继信息?

1.线索二叉树的分类：（根据遍历的不同要求 ）

2.线索二叉树的链式存储

3.怎么样才能画出中序线索二叉树

怎么看一个结点的前驱和后继：

例2：先序线索二叉树

例3：后序线索二叉树

5.6 哈夫曼树及其应用

1.基本概念

( 1 )路径长度(Path Length) :

( 2 ）【树】的路径长度

( 3 )【结点】的【带权】路径长度：

( 4 )树的带权路径长度WPL

2.哈夫曼树

3.哈夫曼树的构造

4.构造哈夫曼树例题：

5.哈夫曼树应用——哈夫曼树编码

6.构造哈夫曼树编码

例题一：给定权{1,5,7,3}，求哈夫曼树及编码(假定权值就代表该字符名字)。

例题二:哈夫曼编码实现数据压缩，设给出一段报文:CAST CAST SAT AT A TASA

7.什么是前缀编码？【来自百度】

5.7 二叉树、树、森林互相转换

1树的表示法

(1)双亲表示法

(2)孩子表示法

(3)双亲孩子表示

(4)孩子兄弟表示法

2.树、二叉树、森林的转换

(1)树转换成二叉树【步骤】

树转换成二叉树例题：

（2）森林转换成二叉树【步骤】

例题一：森林转换成二叉树

例题二：森林转换成二叉树

（3）二叉树转换成森林【步骤】

例题：二叉树转换成森林

3  树和森林的遍历

（1）先序遍历【树和森林】

（2）后序遍历【树和森林】

 

---

第五章 树和二叉树（2）续：

问题1:如何可唯一地确定一棵二叉树?

答:先序+中序或后序+中序均可唯一地确定一棵二叉树。

问题2:二叉树的二叉树链表存储结构中，有多少个指针域未利用?

答:二叉树的二叉链表存储结构中，有【n+1】个指针域未利用，已经使用的有【n-1】个指针域，共有【2n】个指针域。

5.按层遍历

---

5.5  线索二叉树

☆【原有的孩子指针】指向【前驱、后继】还是【指向左、右孩子】；利用原有的孩子指针指向【直接前驱和后继】，这样的指针称为“线索”。

（1）指向左、右孩子：Itag、rtag为0；（2）指向前驱或者后继：Itag、rtag为1

问题1∶为什么二叉树中加入线索?

答:原来的左、右孩子域有许多空指针又没有利用起来。为了不浪费存存贮空间，【利用原有的孩子指针为空时来存放直接前驱和后继，这样的指针称为“线索”，】

加线索的过程称为【线索化】，加了线索的二叉树，称为线索二叉树，对应的二叉链表称为线索二叉链表。

问题2∶如何在二叉树中加入线索?

答:线索(Thread):指向结点前驱和后继的指针

若结点有左孩子，则Ichild指示其左孩子，否则Ichild中存储该结点的前驱结点的指针;

若结点有右孩子，则rchild指示其右孩子，否则rchild中存储指向该结点的后继结点的指针

 

问题3 :怎样来区分孩子指针域中存放的是左、右孩子信息还是直接前驱或直接后继信息?

答:在二叉链表结点中,增加两个标志域Itag、rtag

1.线索二叉树的分类：（根据遍历的不同要求 ）

( 1 )前序线索二叉树(前序的前驱和后继都要标出)

( 2 )中序线索二叉树(中序的前驱和后继都要标出)

( 3 )后序线索二叉树(后序的前驱和后继都要标出)

2.线索二叉树的链式存储

指向左、右孩子：Itag、rtag为0；

指向前驱或者后继：Itag、rtag为1

3.怎么样才能画出中序线索二叉树

（1）先写出中序遍历的序列

（2）看二叉树结点有没有左、右孩子;有左右孩子Itag、rtag为0；否则，Itag、rtag为1；

（3）无左右孩子的序列，看中序遍历序列的前驱后继.

怎么看一个结点的前驱和后继：

一个结点的前驱和后继：要看遍历后的序列

结点D：前驱是B，后继是A；无左、右孩子

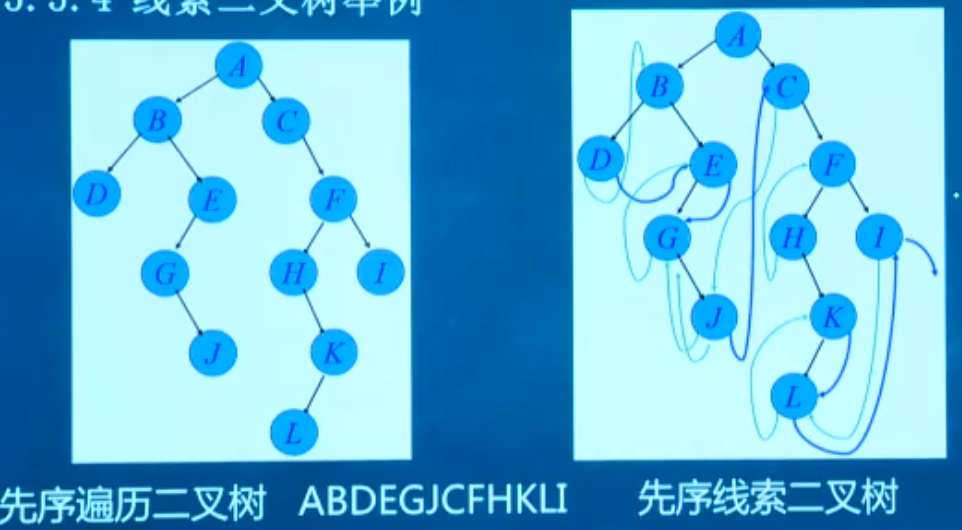
例2：先序线索二叉树

先序遍历：ABDEGJCFHKLI

🔺线索二叉树：把没有左或者右孩子的结点连上它的前驱和后继

例3：后序线索二叉树

5.6 哈夫曼树及其应用

哈夫曼树：是一种最优二叉树

最优二叉树：最优指WPL最小。

1.基本概念

( 1 )路径长度(Path Length) :

【两个结点之间】的路径长度是连接两结点的路径上的【分支数】。

( 2 ）【树】的路径长度

是【各结点】到【根结点】的【路径长度之