Codeforces Round #654 (Div. 2) 题解

最新推荐文章于 2024-08-31 12:42:46 发布

我是个菜鸡.

最新推荐文章于 2024-08-31 12:42:46 发布

阅读量273

点赞数

分类专栏：刷题 FIGHTING

本文链接：https://blog.youkuaiyun.com/weixin_45988242/article/details/107112269

版权

刷题 FIGHTING 专栏收录该内容

20 篇文章

订阅专栏

A题

在这里插入图片描述
题意：给你一个数n，它代表着你有1-n这些数，通过组合（相加的方式），使得相等的数字最多！
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++
思路：想到的肯定就是组合成最大的那一个数啊，但自己第一想法是去算前面的和，这种想法是十分的错误！其实你仔细一想他们不就是收尾对应的数字相加之后就等于那个n嘛？所以呀，代码如下。奇数的时候输出n/2+1，否则输出n/2；

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<string>
#include<iomanip>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
int main()
{
    int t; cin >> t;
    while (t--)
    {
        int n; cin >> n;
        if (n % 2 == 0)
        {
            cout << n / 2 << endl;
        }
        else
        {
            cout << (n + 1) / 2 << endl;
        }
    }
    
}

B题

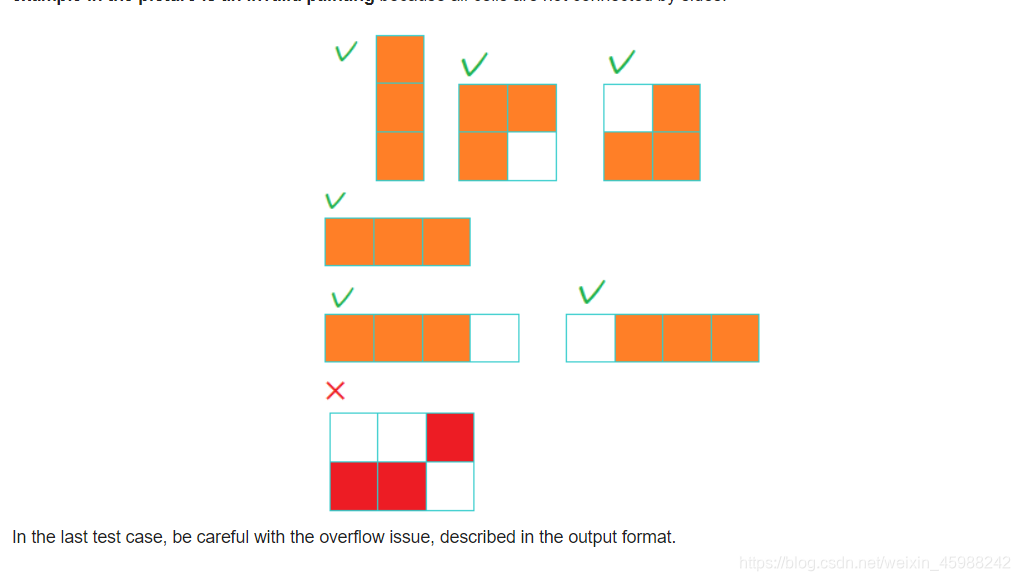
在这里插入图片描述

分析：
B题分析！！

题意：就是相当于给定格子，
让你确定一个起点，画一段连续的天数，超了就下一行
给你一个r,1<=k<=r
问最多有多少种种类的形状
思路：当取到的k>=n时，只有1个，且之后的是重复的
当取到的k<n时，当k为多少时，就有多少个。这样合起来是个等差的求和
比如k=2和k=3，是肯定不会有重复地方的，因为列数不同。因为k<n,所以肯定至少2行，然后把上一行最前面的移到下面的后一位，这样下来有多少个就是当k为一个具体数字的时候的种类数实际上每周的天数决定的是表格的宽度，而表格的长度是无限的。对于天数小于每周天数的情况，那么只能涂在同一行了，总的个数就是1。对于大于每周天数的情况，第一周的选择可以是只涂最后一格、只涂最后两格…涂满整周，每种涂法形状都不同，因此答案就是每周的天数r。那么从1到r，我们只需分类讨论一下就完事了

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<string>
#include<iomanip>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
int main()
{
    int t; cin >> t;
    while (t--)
    {
        ll n, r; cin >> n >> r;
        if (n > r)
        {
            cout << r * (r + 1) / 2 << endl;
        }
        else
        {
            cout << n * (n - 1) / 2 + 1 << endl;
        }
    }
    
}

C题

在这里插入图片描述
题意：两种糖果和两种人，数量分别是 a,b,n,m;吃糖果有条件
第一种人：若第一种糖果数量>第二种，它吃第一种糖果，反之吃第二种糖果；
第二种人：先吃最少的糖果，然后再去吃多的。
思路：首先你的糖果数量必须得多于人的数量！你仔细分析想一下，第一种人，它可以先吃多的再吃少的，所以他可以一直保持糖果平衡，就是只要糖果数量大于第一种人，那么第一种人全都有糖果，所以不用管他，但是第二种人是吃最少的糖果，所以这就要求糖果最小值不小于第二种人。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<string>
#include<iomanip>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
int main()
{
    int t; cin >> t;
    while (t--)
    {
        ll a, b, n, m;
        cin >> a >> b >> n >> m;
        if ((a + b) < (m + n))
        {
            cout << "No" << endl;
        }
        else
        {
            if (m > min(a, b))
            {
                cout << "No" << endl;
            }
            else cout << "Yes" << endl;
        }
    }
    
}

D题

题意:
给你k个1，让你构造出一个n*n的二维数组，使得数组中列和的最大值-列和的最小值的平方 + 行和的最大值 - 行和的最小值的平方最小。
思路：首先你考虑他的输出的那个F是多少，如果k%n==0 那么F=0；
否则一定是F=2；就这两种，问题是那个表怎么输出其实就是按照一定的规律去把一些位置变成1就行。平均摊！
在这里插入图片描述
如图所示，设ans=k/n，这代表一行多少个，y=k%n，代表多出来的那几个，多出来的那几个就让前y行都放 ans+1个1就行，然后y以后就每行放ans个就行，然后从第几个开始放1呢，第i行从第i列开始放1就行了，其中你在放1的时候列可能会超过n那你就再从左边放1就行了呀！

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<string>
#include<iomanip>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
int a[302][322];
int main()
{
    int t; cin >> t;
    while (t--)
    {
        
        int n, k; cin >> n >> k;
        int ans = k / n;
        int y = k % n;
        if (y== 0)
            cout << 0 << endl;
        else cout << 2 << endl;
        
        for (int i = 1; i <=y; i++)
        {
            for (int j=i; j <=i+ans; j++)
            {
                if (j<=n)
                {
                    a[i][j] = 1;
                }
                else
                {
                    a[i][j-n] = 1;
                }
            }
        }
        for (int i = y+ 1; i <=n; i++)
            for (int j = i; j <i+ans; j++)
            {
                if (j <= n)
                {

                    a[i][j] = 1;
                }
                else
                {
                    a[i][j - n] = 1;
                }
            }
        for (int i = 1; i <= n; i++)
        {
            for (int j = 1; j <= n; j++)
            {
                cout << a[i][j];
            }
            cout << endl;
        }
        memset(a, 0, sizeof a);
    }
    
}

ps：D题思路https://blog.youkuaiyun.com/jziwjxjd/article/details/107076412

E1题

在这里插入图片描述
题目大意：你有n个敌人，每个敌人手中有a[i]个糖果，你初始的时候有x个糖果，现在你要和敌人对战，你可以决定敌人的排列顺序，其决战的规则为：你手中的糖果大于等于敌人的，则获胜，且额外获得一颗糖果。你要战胜所有的敌人。定义f(x)为当初始有x个糖果时有f(x)中排列使得你全胜，当f(x)modp=0 这个答案是不够优秀的，反之则是优秀的，问你有多少个优秀的答案，并将其输出。
/思路：设 a数组的最大值为 m ,如果 x >=m 随便怎么放都是可行的，所以置换数位 n！，而 n!%p一定等于 0，所以一定不满足。
而如果 x+n-1< m,最后的值达不到 m 是没有满足的置换的，0%p=0 ,所以也不满足。
所以只要枚举 x-n-1 到 m 求出每个 f（x）,看是否满足题意。复杂度（nn）;
求 f(x) ,总共有 n 个位置从 m-n+1 到 m ，对应的值分别为 x到 m 。所以贪心的从大的开始安排，每个 a[i]只能安排到对应值比a[i]大或者等于的位置。把最大的安排到可以满足的位置一共 x+n-a[i] 个第二大的数有 x+n-1-a[i]个位置。当 a[i]<=x 可以随便放。最后看所有可能是否可以整除 p。*/

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<string>
#include<iomanip>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
const int maxn=2e3+7;
typedef long long ll;
int T,n,p;
int a[maxn];
vector < int > ans;

int f(int x){
    int sum=n,ans=1;
    for(int i=1;i<=n;i++){
        if(a[i]<=x){
           ans=(ans*sum)%p;
        }
        else if(x+sum-a[i]<=0) return 0;
        else ans=(ans*(x+sum-a[i]))%p;
        sum--;
    }
    if(ans==0) return 0;
    return 1;
}
int main(){
         cin>>n>>p;
         for(int i=1;i<=n;i++){
             scanf("%d",&a[i]);
         }
         sort(a+1,a+n+1);
         reverse(a+1,a+n+1);
         int m=a[1];
         for(int i=max(1,m-n+1);i<m;i++){
             if(f(i)) ans.push_back(i);
         }
         cout<<ans.size()<<endl;
         for(auto i: ans) cout<<i<<" ";
         cout<<endl;
}