软件设计师备考笔记（十七）数据结构及算法应用

概述

• 主要为了应对下午题；下午题 的难点；

• 要扎实基本功；

• 所以策略不同（稳拿部分分数，其他要求拿高分）

目录

• 分治法

• 回溯法

• 贪心法

• 动态规划法

学习要求

• 算法种类了解覆盖95%以上；

• 问什么算法能答出来；

• 给数据能给结果；

分治法

• 把大问题拆分成多个子问题；

• 能用到递归技术解决的问题；

  • 拆分后要和原来一样结构只是复杂的小些、规模小些；

  • 子问题也要能用同样方式拆分；

• 思路：解决小问题；一步一步合并，得到初始问题的解决方案；

对问题的要求

递归技术

• 辅助理解：

  • 上述算法功能： 求有序数列的第N项值是什么；

  • 上方表示数列的值；下方表示第几位数；

• 关键点：复杂问题要能拆分为同样结构的子问题；

二分查找

回溯法

贪心法

• 判断是否是贪心法：是不是每一步都最优 ，但结果不是最优；

• （b）左边：贪心法；右边：最优解；

• （c）能重复装的情况下最优解；

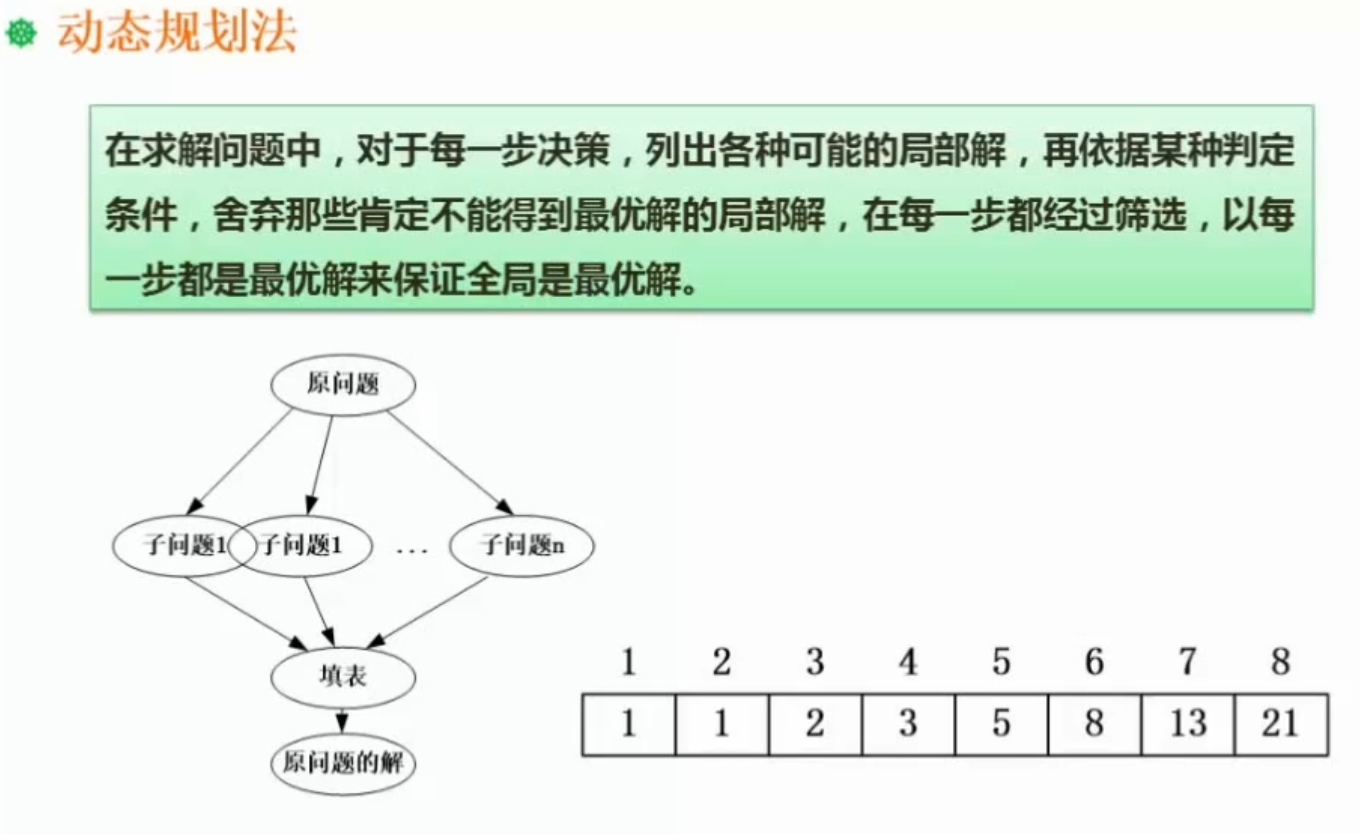
动态规划法

• 和分治法比较像；

• 如何识别？

  • 动态规划都要用查表的方式，把子问题拆分后子问题不一定是独立的，要求更复杂问题解时，通过查找表解决；

例子：

和分治法一样，计算有序数列的第N个数是什么；此时实际上就是存储一张表，如图右下角，计算第N个数时就查找N-1个数和N-2个数的是什么；

试题

试题1

先不填写代码，做其他题目加深理解

问题2：

最先：贪心法，用最小的代价找到能装下的位置；

最优：贪心法；用最小的空间装完所有货物；

时间复杂度：以算法中最高复杂的当作算法的最高复杂的；

左右都是嵌套循环为最高复杂的所以都是O（n^2）

问题1：

（1）j=0；

（2）b[j]=b[j]+S[i[

（3）min=temp;

（4）b[m]=b[m]+s[i]

试题2

问题2：

分治法；

递归式（偏数学化），怎么写？一分为2；所以T(n)=2T(n/2)；全部代码中，最高时间复杂度为O(n)所以为T(n)=2T(n/2)+O(n);这样下来时间复杂度约为O(nlogN);

有多少个元素就涉及多少个交换空间所以 空间复杂度为 O(n)

问题3：必须先解决源码才能做第三题；（做题时分析全部题目再看先后顺序；）

归并排序时，比较次数是n1+n2次；

问题1

（1）k<=r

（2）arr[k]=right[j]

（3）

（4）

void mergeSort函数时归并排序的递归部分；