蓝桥杯真题详细题解——持续更新

目录

一、方格分割

二、组队

---

一、方格分割

题目描述：

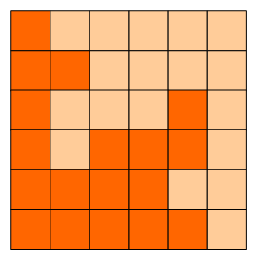
6x6的方格，沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。

如图：p1.png, p2.png, p3.png 就是可行的分割法。

试计算：
包括这3种分法在内，一共有多少种不同的分割方法。
注意：旋转对称的属于同一种分割法。

代码如下：

#include<iostream>
using namespace std;
int ans;
int dire[][2]={{-1,0},{1,0},{0,-1},{0,1}};
int vis[7][7];
void dfs(int x,int y)
{
	if(x==0||x==6||y==0||y==6)
	{
		ans++;
		return;
	}
	vis[x][y]=1;
	vis[6-x][6-y]=1;
	for(int k=0;k<4;k++)
	{
		int nx=x+dire[k][0];
		int ny=y+dire[k][1];
		if(nx<0||nx>6||ny<0||ny>6)
			continue;
		if(!vis[nx][ny])
		{
			dfs(nx,ny);
		}
	}
	vis[x][y]=0;
	vis[6-x][6-y]=0;
}
int main()
{
	dfs(3,3);
	printf("%d\n",ans/4);
	return 0;
}

运行结果：

声明：

此题代码完全搬运于蓝桥学苑，只为日后复习使用。

二、组队

题目描述：

作为篮球队教练，你需要从以下名单中选出 1 号位至 5 号位各一名球员， 组成球队的首发阵容。 每位球员担任 1 号位至 5 号位时的评分如下表所示。请你计算首发阵容 1 号位至 5 号位的评分之和最大可能是多少？

代码如下：

#include<bits/stdc++.h>
using namespace std;
int queen[5],visited[20];
int x[20][5]={
{97,90,0,0,0},
{92,85,96,0,0},
{0,0,0,0,93},
{0,0,0,80,86},
{89,83,97,0,0},
{82,86,0,0,0},
{0,0,0,87,90},
{0,97,96,0,0},
{0,0,89,0,0},
{95,99,0,0,0},
{0,0,96,97,0},
{0,0,0,93,98},
{94,91,0,0,0},
{0,83,87,0,0},
{0,0,98,97,98},
{0,0,0,93,86},
{98,83,99,98,81},
{93,87,92,96,98},
{0,0,0,89,92},
{0,99,96,95,81},};
int maxn;
void dfs(int number)
{
	int i,sum=0;
	if(number==5)				//五位队员选取完毕 
	{
		for(i=0;i<5;i++)		//计算队伍总得分 
		{
			sum+=queen[i];
		}
		if(sum>maxn)			//比较目前最高分和此队伍总得分 
		{
			maxn=sum;
		}
	}
	else
	{
		for(i=0;i<20;i++)
		{
			if(!visited[i])			
			{
				queen[number]=x[i][number];
				visited[i]=1;	//每位选手只能担任一个位置 
				dfs(number+1);	//选区下一号位选手 
				visited[i]=0;	
			}
		}
	}
}
int main()
{
	dfs(0);						//从1号位开始选取 
	printf("%d\n",maxn);	 
	return 0; 
} 

运行结果：

三、完全二叉树的权值

完全二叉树的权值——C++详解