Codeforces Round #736 (Div. 2)题解_codeforces round 736 (div. 2)-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_45948940/article/details/119810703

这篇博客探讨了在信息技术领域中，数学和算法如何解决复杂问题。通过分析不同类型的题目，如同余问题、棋盘游戏策略、图论问题和组合计数等，展示了数学和算法在求解实际问题中的重要作用。文章提供了简洁的代码实现，阐述了如何运用数学思想和贪心策略来优化解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1549/problem/A Gregor and Cryptography
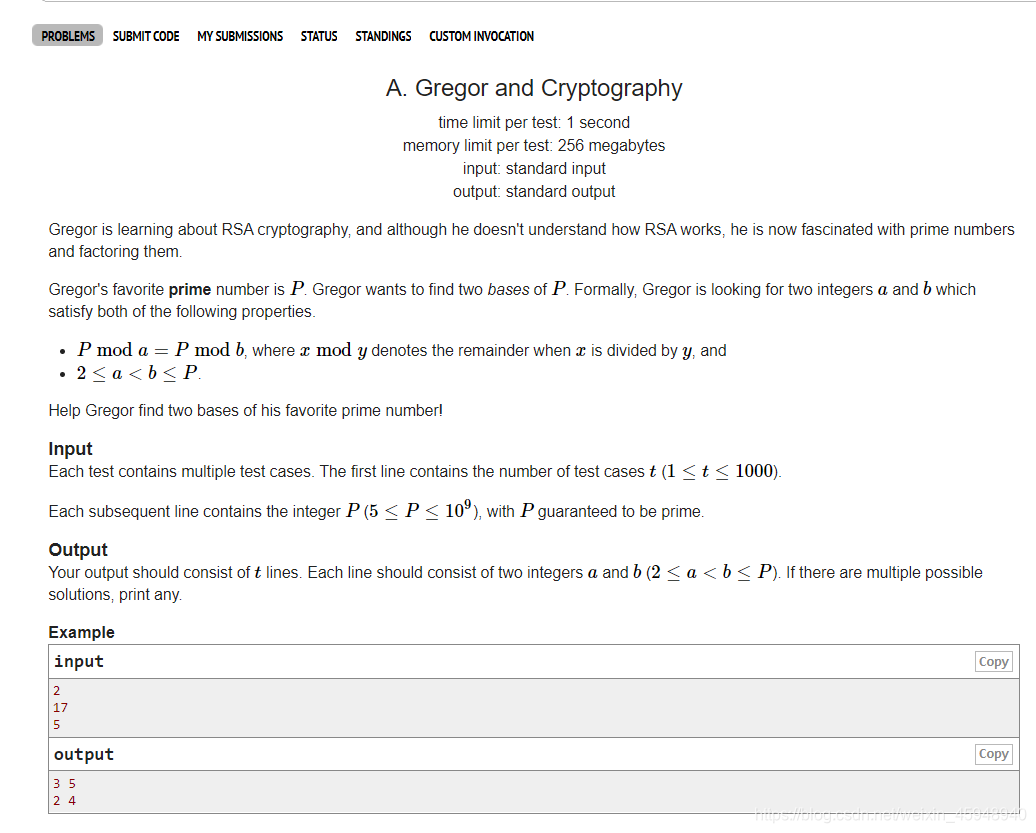
在这里插入图片描述
题意：对于给出的p求解一组a,b满足上述同余条件。输出一组解即可。
分析：我们从奇数偶数的角度来思考。如果p是偶数，那么p模自己和p模2都是整除且合理。如果p是奇数，那么考虑p模2和p模(p-1)都是同余的。


signed main()
{
    ll t;
    read(t);
    while(t--)
    {
        ll p;
        read(p);
        if(p%2==1)
        {
            printf("2 %lld\n",p-1);
        }
        else
        {

            printf("2 %lld\n",p);

        }

    }

}

Gregor and the Pawn Game题目
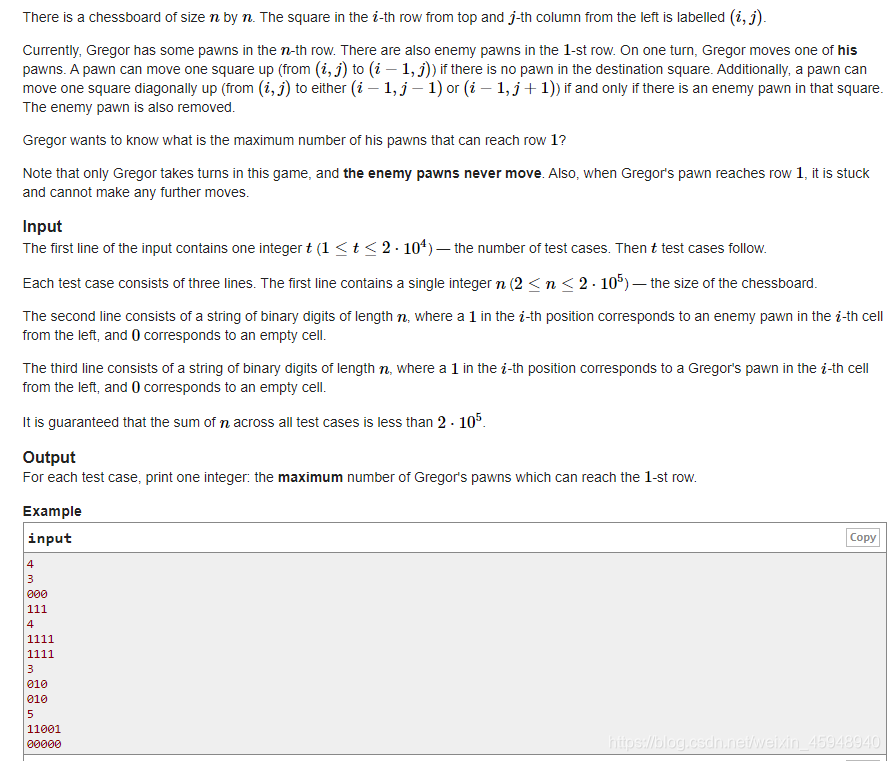
在这里插入图片描述
直接模拟贪心就行了。

char s[222222];
char b[222222];
signed main()
{
    ll t;
    read(t);
    while(t--)
    {
        ll n;
        read(n);
        scanf("%s%s",s+1,b+1);
        ll ans=0;
        for(int i=1; i<=n; i++)
        {

            if(s[i]=='0'&&b[i]=='1')
            {
                ans++;
                s[i]='2';
                continue;
            }
            if(s[i-1]=='1'&&b[i]=='1')
            {
                ans++;
                s[i-1]='2';
                continue;
            }
            if(s[i+1]=='1'&&b[i]=='1')
            {
                ans++;
                s[i+1]='2';
                continue;
            }

        }
        printf("%lld\n",ans);
    }

}

Web of Lies 题目
大概是在讲如果两个点u,v连在一起，那么较大的那个会被杀掉。询问一系列操作后能剩下多少个点。其实每次只需要标记一下每个点的连边情况就行了，如果u,v给小点打上标记。最终没被标记的点就是可以剩下的点。

在这里插入图片描述

ll d[222222];
signed main()
{

    ll n,m;
    ll ans=0;
    read(n);
    read(m);
    for(int i=1; i<=m; i++)
    {
        ll u,v;
        read(u);
        read(v);
        if(u>v)
        {
            d[v]++;
        }
        else
        {
            d[u]++;
        }

    }
    for(int i=1; i<=n; i++)
    {
        if(d[i]==0)
            ans++;
    }
    ll q;
    read(q);
    while(q--)
    {
        ll op;
        read(op);
        if(op==3)
        {
            printf("%lld\n",ans);
            continue;
        }
        ll u,v;
        read(u);
        read(v);
        if(op==1)
        {
            if(u>v)
            {
                if(d[v]==0)
                {
                    ans--;
                }
                d[v]++;
            }
            else
            {
                if(d[u]==0)
                {
                    ans--;
                }
                d[u]++;
            }
            continue;
        }
        if(u>v)
        {
            d[v]--;
            if(d[v]==0)
                ans++;
        }
        else
        {
            d[u]--;
            if(d[u]==0)
                ans++;
        }
    }

}

Integers Have Friends 题目
在这里插入图片描述
题意：求解最长的连续同余序列。
分析：考虑到同余，那么两个数的差一定是该余数的倍数。考虑到求一段连续的，那么只需要给两两数做差分，对差分序列套个区间gcd。枚举起点i，从i+1到n二分第一个gcd为1的点，终止，记录答案。为什么要从i+1开始呢，因为i+1差分才包含第i个数。

ll a[maxn],b[maxn];
ll dp[maxn][60];
void rmq(){
 
    for(int i=1;i<=n;i++){
        dp[i][0]=b[i];
    }
    for(int j=1;(1<<j)<=n;j++){
        for(int i=1;i+(1<<j)-1<=n;i++){
            dp[i][j]=__gcd(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
        }
    }
}
ll query(int l,int r){
    int k=log2(r-l+1);
    return __gcd(dp[l][k],dp[r-(1<<k)+1][k]);
}
int main(){
    int _;cin>>_;
    while(_--){
        cin>>n;
        for(int i=1;i<=n;i++){
            cin>>a[i];
            b[i]=abs(a[i]-a[i-1]);
        }
        rmq();
        int pr=0;
        for(int i=1;i<=n;i++){
            int l=i+1,r=n,ans=i;
            while(l<=r){
                int mid=(l+r)/2;
                if(query(i+1,mid)>1){
                    ans=mid;
                    l=mid+1;
                }else{
                    r=mid-1;
                }
            }
            pr=max(pr,ans-i+1);
        }
        printf("%d\n",pr);
    }
    return 0;
}

The Three Little Pigs 题目
题目大意：

有n min 每分钟会进来三个不同的小猪，大灰狼要吃x个小猪，问大灰狼有多少种吃法。

分析：
对于一个x ，它与x+0 ,x+1 ,x+2 可以划分为一组，该组的计算方式一致，均为Σ C(i3,x+m).记dp[x][m]=Σ C( i * 3+m,x)
易得dp[x][0]+dp[x][1]+dp[x][2]= Σ C( i * 3,x)+ Σ C( i * 3+1,x)+Σ C( i * 3+2,x)
因为 C(a,b)=C(a−1,b−1)+C(a−1,b)
因为dp[x][0]+dp[x][1]+dp[x][2]=Σ_i=0^i=3*n-1C(i,x) =C(3n,x+1)
易得dp[x][1]=dp[x][0]+dp[x-1][0] 同理dp[x][2]=dp[x][1]+dp[x-1][1]
解方程可以求出dp[x][0]

 #include<bits/stdc++.h>
#include<stdlib.h>
#include<algorithm>
#include<stdio.h>
#include<string.h>
#include<queue>
#include<time.h>
#include <cstdio>
#include <iostream>
#include <vector>
#define ll long long
#define int long long
#define inf 0x3f3f3f3f
#define mods 1000000007
#define modd 998244353
#define PI acos(-1)
#define fi first
#define se second
#define lowbit(x) (x&(-x))
#define mp make_pair
#define pb push_back
#define si size()
#define E exp(1.0)
#define fixed cout.setf(ios::fixed)
#define fixeds(x) setprecision(x)
#define IOS ios::sync_with_stdio(false);cin.tie(0)
 using namespace std;
 ll gcd(ll a,ll b){if(a<0)a=-a;if(b<0)b=-b;return b==0?a:gcd(b,a%b);}
template<typename T>void read(T &res){bool flag=false;char ch;while(!isdigit(ch=getchar()))(ch=='-')&&(flag=true);
for(res=ch-48;isdigit(ch=getchar());res=(res<<1)+(res<<3)+ch - 48);flag&&(res=-res);}
ll lcm(ll a,ll b){return a*b/gcd(a,b);}
ll qp(ll a,ll b,ll mod){ll ans=1;if(b==0){return ans%mod;}while(b){if(b%2==1){b--;ans=ans*a%mod;}a=a*a%mod;b=b/2;}return ans%mod;}//快速幂%
ll qpn(ll a,ll b, ll p){ll ans = 1;a%=p;while(b){if(b&1){ans = (ans*a)%p;--b;}a =(a*a)%p;b >>= 1;}return ans%p;}//逆元   (分子*qp(分母,mod-2,mod))%mod;



/*N<=1e6,利用费马小定理*/
#define LL long long
const int MX = 4030000 + 5;
const int mod = 1e9 + 7;
LL F[MX], invF[MX];
LL power(LL a, LL b) {
    LL ret = 1;
    while(b) {
        if(b & 1) ret = (ret * a) % mod;
        a = (a * a) % mod;
        b >>= 1;
    }
    return ret%mod;
}
void init() {
    F[0] = 1;
    for(int i = 1; i < MX; i++){
        F[i] = (F[i - 1] * i) % mod;
}
    invF[MX - 1] = power(F[MX - 1], mod - 2);
    for(int i = MX - 2; i >= 0; i--) {
        invF[i] = invF[i + 1] * (i + 1) % mod; //invF[i]*i!=1,invF[i+1]*i!*(i+1)=1
    }
}

LL C(int n, int m) {
    if(n < 0 || m < 0 || m > n) return 0;
    if(m == 0 || m == n)    return 1;
    return F[n] * invF[n - m] % mod * invF[m] % mod;
}
LL A(int n, int m) {
    if(n < 0 || m < 0 || m > n) return 0;
    return F[n] * invF[n - m] % mod;
}

ll dp[3003010][4];
signed main(){

    init();
    ll n,m;
    read(n);
    read(m);
    dp[0][0]=n;
    dp[0][1]=n;
    dp[0][2]=n;
    ll op=qp(3,mods-2,mods)%mods;
    for(int i=1;i<=3*n-1;i++){

    dp[i][0]=(((C(3*n,i+1)-2*dp[i-1][0]-dp[i-1][1])%mods+mods)%mods*op%mods)%mods;
    dp[i][1]=(dp[i-1][0]%mods+dp[i][0]%mods)%mods;
    dp[i][2]=(dp[i-1][1]%mods+dp[i][1]%mods)%mods;
    }
    while(m--){
        ll x;
        read(x);
        printf("%lld\n",(dp[x][0]%mods+C(3*n,x)%mods)%mods);

    }


}