平衡二叉树
平衡二叉树(Self-Balancing Binary Search Tree 或 Height-Balanced Binary Search Tree)是一种二叉排序树,其中每一个节点的左子树和右子树的高度差至多等于1。
它是一种高度平衡的二叉排序树。它要么是一棵空树, 要么它的左子树和右子树都是平衡二叉树,且左子树和右子树的深度之差的绝对值不超过1。我们将二叉树上结点的左子树深度减去右子树深度的值称为平衡因子BF (Balance Factor) , 那么平衡二叉树上所有结点的平衡因子只可能是-1、0和1。只要二叉树上有一个结点的平衡因子的绝对值大于1,则该二叉树就是不平衡的。
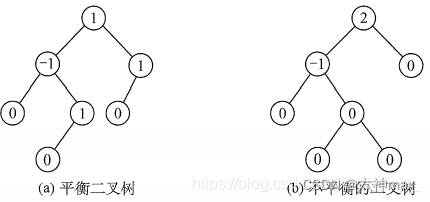
二叉排序树保证平衡的基本思想如下:每当在二叉排序树中插入(或删除)一个结点时,首先检查其插入路径上的结点是否因为此次操作而导致了不平衡。若导致了不平衡,则先找到插入路径上离插入结点最近的平衡因子的绝对值大于1的结点A,再对以A为根的子树,在保持二叉排序树特性的前提下,调整各结点的位置关系,使之重新达到平衡。
失衡的二叉树种类有:
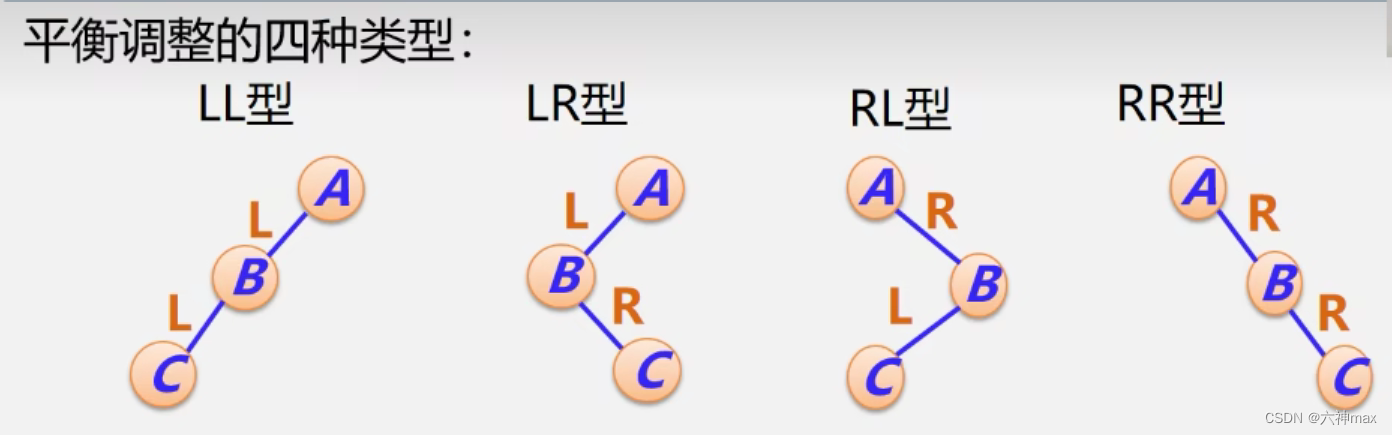
分别调整成如下情况:
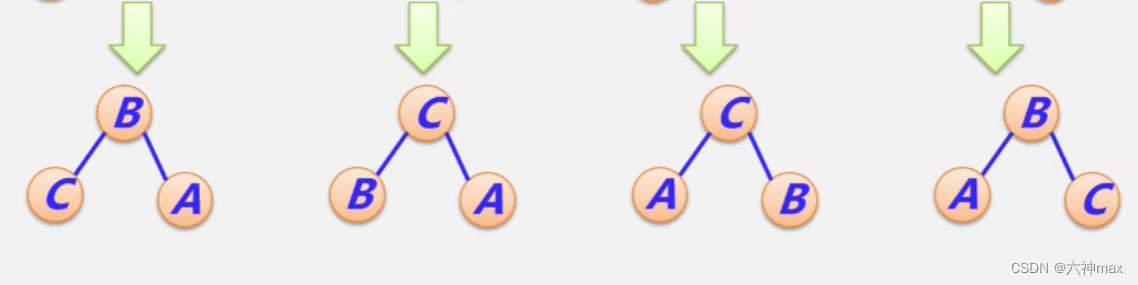
这样就又重新回到了平衡二叉树。
LL型调整过程:
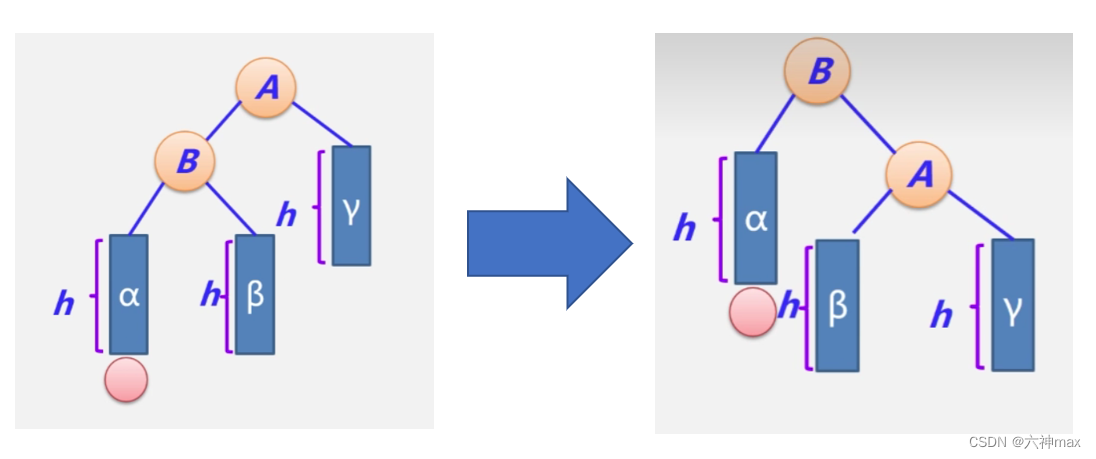
- B结点带左子树α一起上升
- A结点称为B的右孩子
- 原来B结点的右子树β作为A的左子树
RR型调整过程:
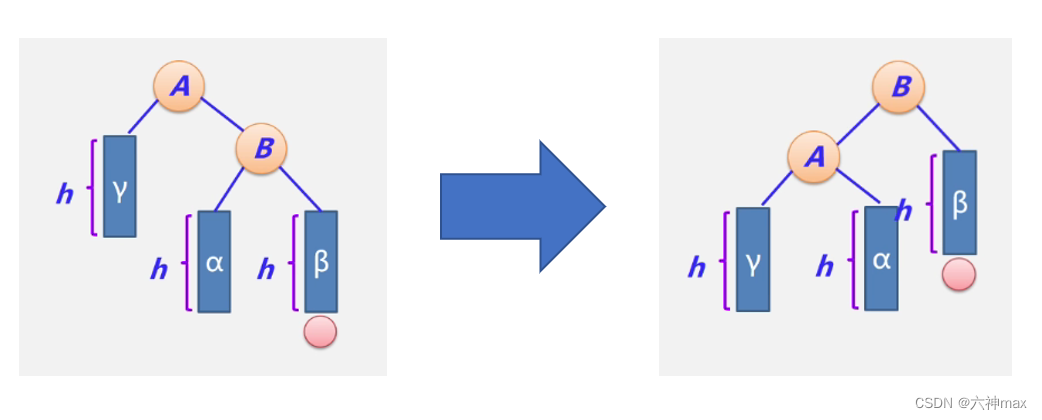
- B结点带右子树β一起上升
- A结点成为B的左孩子
- 原来的B结点的左子树α作为A的右子树
LR型调整过程:
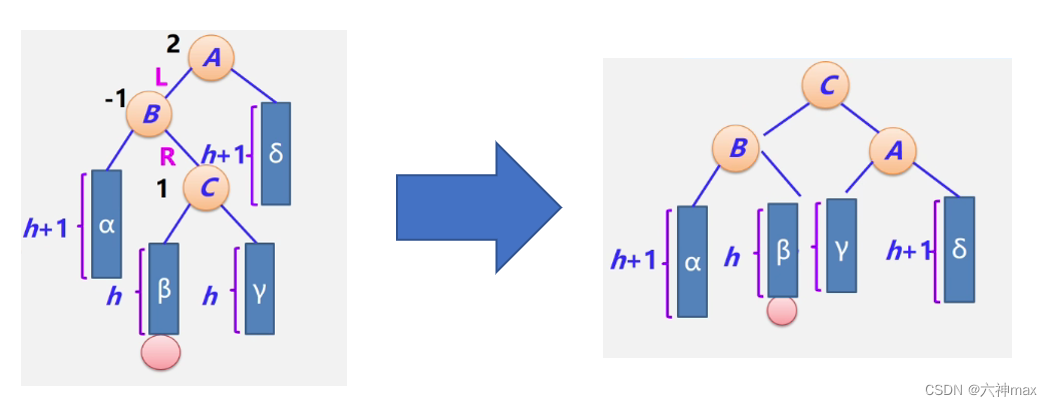
- C结点穿过A、B结点上升
- B结点成为C的左孩子
A结点成为C的右孩子 - 原来C结点的左子树β作为B的右子树
原来C结点的右子树γ作为A的左子树
RL型调整过程:
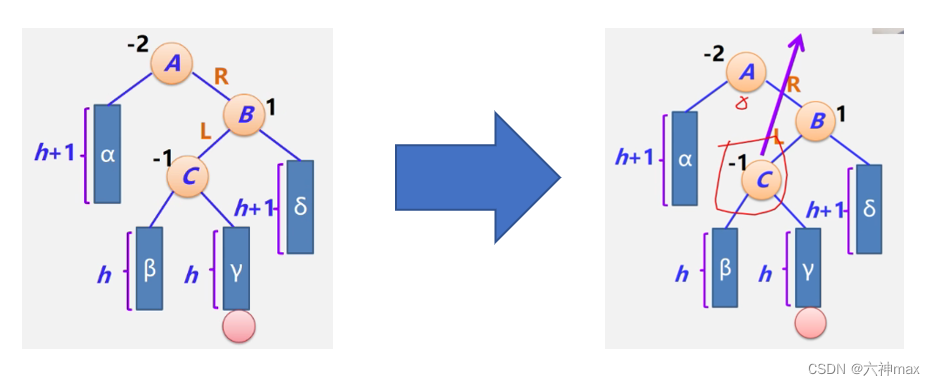
- C结点穿过A、B结点上升
- B结点成为C的右孩子
A结点成为C的左孩子 - 原来C结点的左子树β作为A的右子树
原来C结点的右子树γ作为B的左子树
RL型调整例题:
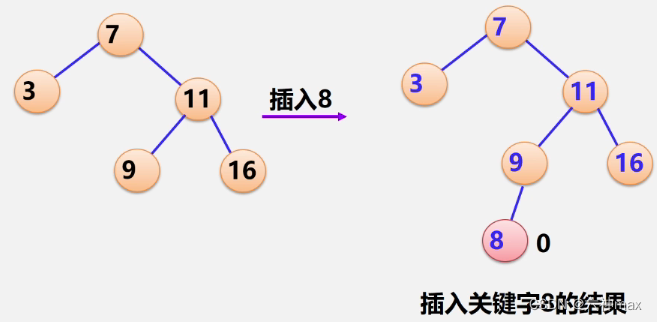
插入之后,会出现失衡的现象,现在就进行平衡二叉树的调整:
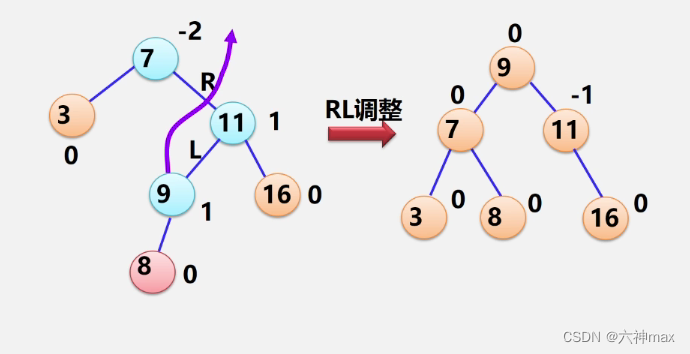





 平衡二叉树是一种特殊的二叉排序树,确保左右子树高度差不超过1,以维持高效查找性能。当插入或删除节点导致不平衡时,通过LL、RR、LR和RL四种调整方式恢复平衡。这些调整策略确保了树的平衡状态,维持了二叉排序树的特性。
平衡二叉树是一种特殊的二叉排序树,确保左右子树高度差不超过1,以维持高效查找性能。当插入或删除节点导致不平衡时,通过LL、RR、LR和RL四种调整方式恢复平衡。这些调整策略确保了树的平衡状态,维持了二叉排序树的特性。

















 424
424

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








