初识反向传播

引入

在单层感知机模型中，对于输入与输出之间的权重调整依赖于预测产生的误差，由于不含隐藏层，误差可以直接计算得到。而对于多层网络来说，由于隐藏层的存在，输入输出之间的权重变得复杂，显然直接计算并不合理，而是需要通过从输出到输入反方向逐层计算。

由于是从输出到输入，所以我们一定需要先有一个正向传播的过程。使得样本从输入层开始，由上至下逐层经隐节点计算处理，最终样本信息被传送到输出层节点，得到预测的结果。再根据正向传播得到的结果也就是预测经行误差计算。

由于有了误差和输出，以及之前传播过来的网络，就有了反向传播的原材料，可以开始进行反向传播了。反向传播无法直接计算隐节点的预测误差，但却可以利用输出节点的预测误差来逐层估计隐节点的误差，也就是将输出节点的预测误差反方向传播到上层隐节点，逐层调整连接权重，直至输入节点和隐节点的权重全部得到调整，使得网络输出值越来越逼近实际值。

细节

每个神经元都由两个单元组成。第一个单元的功能是把每个输入信号和对应权重系数($w_i$)作乘积然后对这些乘积求和。第二个单元实现了一个非线性函数。这个函数也称为神经元激活函数(neuron activation function)。如下图所示，信号$e$是加法器（即第一个单元）的输出信号，而$y=f(e)$是非线性函数（即第二个单元）的输出信号。显然，$y$也同时是这整个神经元的输出信号。

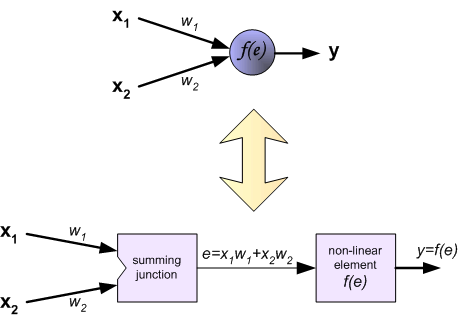
一般这个非线性激活函数采用sigmoid函数。节点的输出被限制在0~1的范围内。对于分类问题，输出节点给出的是预测类别的概率值；对于回归问题，输出节点给出的标准化处理后的预测值，只需还原处理即可。
使用sigmoid的原因：

• 在模型开始训练阶段，由于连接权重的设置要求满足均值为0的均匀分布，所以初期的连接权重在0值附近，使得加法器结果也在0附近。此时sigmoid函数的斜率近似为一个常数，输入输出间呈近似线性关系，模型较为简单；
• 随着模型训练的进行，网络权重不断调整，节点加法器的结果逐渐偏离0值，输入输出逐渐呈现出非线性关系，模型逐渐复杂起来，并且输入的变化对输出的影响程度逐渐减小
• 到模型训练的后期，节点加法器结果远离0，此时输入的变化将不再引起输出的明显变动，输出基本趋于稳定。神经网络的预测误差不再随着连接权重的调整而得到明显改善，预测结果稳定，模型训练结束。

可见，sigmoid激活函数较好的体现了连接权重修正过程中，模型从近似线性到非线性的渐进转变过程。

除此之外，sigmoid激活函数还具有无限次可微的特点，这使得反向传播能够采用梯度下降法来挑战连接权重。

关键过程

由于权重的不同，会导致前置神经元对后续紧邻的后置神经元传递的误差不同，或者说对后置神经元的误差贡献度不同，所以在进行反向传播的时候，不能将误差均分到前置 的神经元，而是应该根据权值对误差进行反向的传递。


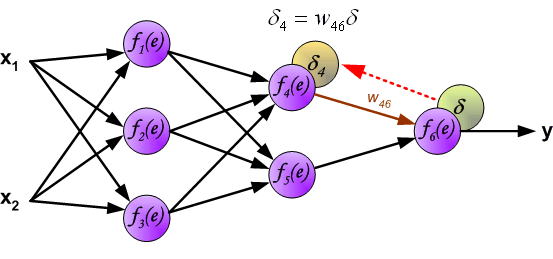
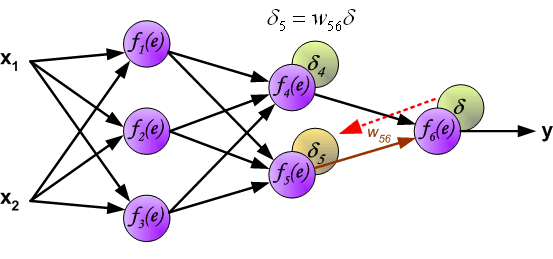
如果前置的神经元对后置多个神经元都传递了误差，那反向传播的时候潜质的误差需要按照权重对后置的误差求和。

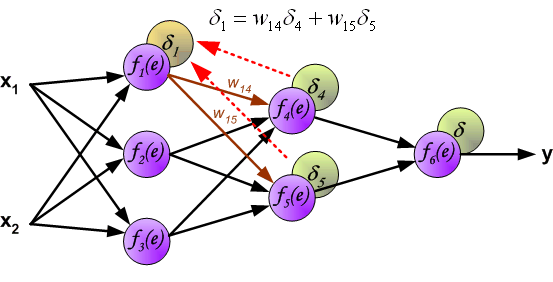
当每个神经元的误差信号都已经被计算出来之后，我们就可以开始修改每个神经元输入结点的权重系数了。在下面的公式中，$\frac{\mathrm{d}{\mathrm{f}}_1(\mathrm{e})}{\mathrm{d}e}$表示对应的神经元激活函数的导数。



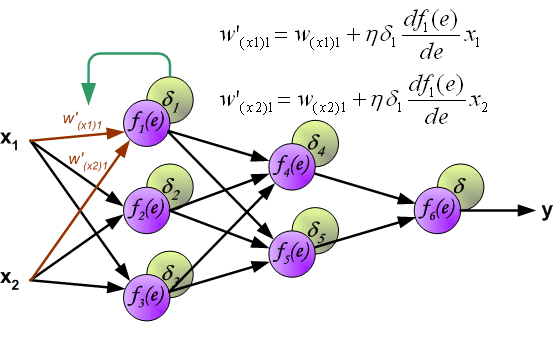
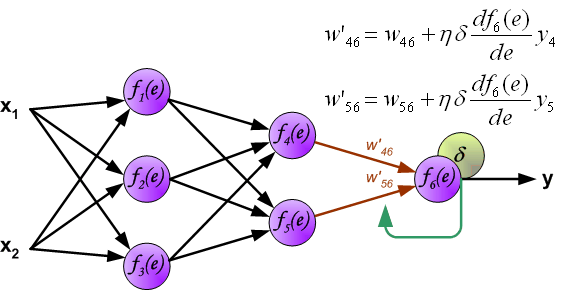
计算是逐层的，这里只展示一条链上（$x_1-->f_{1}e-->f_{4}e-->f_{5}e$）的计算，同层计算方式相同不多描述
具体的调整和计算方法涉及到梯度下降算法
系数$\eta$会影响网络的训练速度。有几种技术可以用于选择系数$\eta$。第一种方法是以较大的参数值开始训练过程。在建立权重系数的同时，参数也逐渐减小。第二种方法更复杂，它以较小的参数值开始训练。在训练的过程中，参数增加，然后在最后阶段参数再次减小。以较小的参数值开始训练使得我们可以确定权重参数的符号。