linear-regression

线性回归

单变量线性回归

• 𝑚 代表训练集中实例的数量
• 𝑥 代表特征/输入变量
• 𝑦 代表目标变量/输出变量
• (𝑥, 𝑦) 代表训练集中的实例 (𝑥 (𝑖) , 𝑦 (𝑖) ) 代表第𝑖 个观察实例
• ℎ 代表学习算法的解决方案或函数也称为假设（hypothesis）

ℎ𝜃 (𝑥) = 𝜃0 + 𝜃1𝑥，因为只含有一个特征/输入变量，因此这样的问题叫作单变量线性回归问题

代价函数cost function

代价函数也被称作平方误差函数，有时也被称为平方误差代价函数。我们之所以要求出 误差的平方和，是因为误差平方代价函数，对于大多数问题，特别是回归问题，都是一个合 理的选择。还有其他的代价函数也能很好地发挥作用，但是平方误差代价函数可能是解决回 归问题最常用的手段了。

梯度下降

梯度下降是一个用来求函数最小值的算法，我们将使用梯度下降算法来求出代价函数 𝐽(𝜃0, 𝜃1) 的最小值。

梯度下降背后的思想是：开始时我们随机选择一个参数的组合(𝜃0, 𝜃1, . . . . . . , 𝜃𝑛 )，计算代 价函数，然后我们寻找下一个能让代价函数值下降最多的参数组合。我们持续这么做直到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确 定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组 合，可能会找到不同的局部最小值。

批量梯度下降（batch gradient descent）算法的公式为：

其中𝑎是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向 向下迈出的步子有多大，在批量梯度下降中，我们每一次都同时让所有的参数减去学习速率 乘以代价函数的导数

有关𝑎的大小

如果𝑎太小了，即我的学习速率太小，结果就是只能这样像小宝宝一样一点点地挪动， 去努力接近最低点，这样就需要很多步才能到达最低点，所以如果𝑎太小的话，可能会很慢， 因为它会一点点挪动，它会需要很多步才能到达全局最低点。

如果𝑎太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移 动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来 机器学习课程-第 1 周-单变量线性回归(Linear Regression with One Variable) 25 越远，所以，如果𝑎太大，它会导致无法收敛，甚至发散。

在梯度下降法中，当我们接近局部最低点时，梯度下降法会自动采取更小的 幅度，这是因为当我们接近局部最低点时，很显然在局部最低时导数等于零，所以当我们接近局部最低时，导数值会自动变得越来越小，所以梯度下降将自动采取较小的幅度，这就是 梯度下降的做法。所以实际上没有必要再另外减小𝑎。

梯度下降的线性回归

“批量梯度下降”，指的是在梯度下降的每一步中，我们都用到了 所有的训练样本，在梯度下降中，在计算微分求导项时，我们需要进行求和运算，所以，在每一个单独的梯度下降中，我们最终都要计算这样一个东西，这个项需要对所有𝑚个训练样本求和。

因此，批量梯度下降法这个名字说明了我们需要考虑所有这一"批"训练样本，而事实上，有时也有其他类型的梯度下降法，不是这种"批量"型的，不考虑整个的训练集，而是机器学习课程每次只关注训练集中的一些小的子集。

小练习

假设你是某公司的CEO，正在考虑在不同的城市开设一家新的分店。连锁店已经在不同的城市有分店，你有数据来自那些城市的利润和人口。您可以使用此数据来帮助您选择要增设分店的城市。

matlab

data = load('ex1data1.txt'); %导入数据
X = data(:,1); %X表示第一列数据即人口
Y = data(:,2); %Y表示第二列数据即利润
m = length(Y);%样本数量
plot(X,Y,'rx','MarkerSize',10); %可以画出人口和利润相关的二维图像
ylabel('profit in $10,000s');
xlabel('population of city in 10,1000s');

X = [ones(m,1),data(:,1)];%在X增设一列全1，用于后续点乘方便
theta = zeros(2,1); %初始化一个1列2行的theta向量
iterations = 1500;%迭代次数
alpha = 0.01;%学习率
 
J = ComputeCost(X, Y, theta); %计算theta为[0,0]时候cost function
fprintf('With theta = [0 ; 0]\nCost computed = %f\n', J);

J = ComputeCost(X, Y, [-1 ; 2]);%计算theta为[-1,2]时候cost function
fprintf('\nWith theta = [-1 ; 2]\nCost computed = %f\n', J);

%梯度下降应用
theta = gradientDescent(X, Y, theta, alpha, iterations);
fprintf('%f\n', theta);

hold on; 
plot(X(:,2), X*theta, 'b-') %在之前的画布上继续画上回归线
legend('Training data', 'Linear regression') %图例
hold off 

predict1 = [1, 3.5] * theta; %预测人口3.5万和7万的利润
predict2 = [1, 7] * theta;


%画图 J与theta0和theta1的Surface plot和Contour plot
theta0_vals = linspace(-10, 10, 100);
theta1_vals = linspace(-1, 4, 100);

J_vals = zeros(length(theta0_vals), length(theta1_vals));
% Fill out J_vals
for i = 1:length(theta0_vals)
    for j = 1:length(theta1_vals)
	  t = [theta0_vals(i); theta1_vals(j)];
	  J_vals(i,j) = ComputeCost(X, Y, t);
    end
end

J_vals = J_vals';
% Surface plot
figure;
surf(theta0_vals, theta1_vals, J_vals)
xlabel('\theta_0'); ylabel('\theta_1');

% Contour plot
figure;
contour(theta0_vals, theta1_vals, J_vals, logspace(-2, 3, 20))
xlabel('\theta_0'); ylabel('\theta_1');
hold on;
plot(theta(1), theta(2), 'rx', 'MarkerSize', 10, 'LineWidth', 2);

function J = ComputeCost(X, y, theta)

m = length(y); 
J = 0;
predictions = X * theta; %m*n维 n*1维 
sqrErrors = (predictions - y) .^ 2; %平方
J = 1 / (2 * m) * sum(sqrErrors);

end

function [theta, J_history] = gradientDescent(X, y, theta, alpha, num_iters)

m = length(y);%先求样本数量
%生成一个初始所有值为0的元素数量为num_iters的向量记录J的变化
J_history = zeros(num_iters,1); 
%进行num_iters次循环算J
for iter = 1:num_iters,
    %生成一个向量记录theta
    theta_temp = theta;
    %对theta每一个元素进行更新
    for j=1:length(theta)
        theta_temp(j) = theta(j)-alpha/m*(X*theta-y)'*X(:,j);
    end
    %更新theta
    theta = theta_temp;
    %计算此次梯度下降的J
    J_history(iter) = ComputeCost(X,y,theta);
end
end

python

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12,8))
plt.show()
# 新增一例，x0
data.insert(0, 'Ones', 1)

cols = data.shape[1]
X = data.iloc[:, 0:cols-1]
Y = data.iloc[:, cols-1:cols]

X = np.matrix(X.values)
Y = np.matrix(Y.values)
theta = np.matrix(np.array([0, 0]))

# 代价函数
def computeCost(X, Y, theta):
    inner = np.power((X * theta.T) - Y, 2)
    return np.sum(inner) / (2 * len(X))

computeCost(X, Y, theta)
#32.072733877455676

# 梯度下降
def gradientDescent(X, Y, theta, alpha, iters):
    temp = np.matrix(np.zeros(theta.shape))
    parameters = int(theta.shape[1])
    cost = np.zeros(iters)
    
    for i in range(iters):
        error = X * theta.T - Y
        
        for j in range(parameters):
            term = np.multiply(error, X[:, j])
            temp[0, j] = temp[0, j] - alpha / len(X) * np.sum(term)
        
        theta = temp
        cost[i] = computeCost(X, Y, theta)
    
    return theta, cost

alpha = 0.01
iters = 1500
g, cost = gradientDescent(X, Y, theta, alpha, iters)
g
#matrix([[-3.63029144,  1.16636235]])

# 计算训练模型的误差
computeCost(X, Y, g)
#4.483388256587726


# 画出拟合图像
x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = g[0, 0] + g[0, 1] * x

plt.figure(figsize=(12, 8))
plt.xlabel('Population')
plt.ylabel('Profit')
l1 = plt.plot(x, f, label='Prediction', color='red')
l2 = plt.scatter(data.Population, data.Profit, label='Traing Data', )
plt.legend(loc='best')
plt.title('Predicted Profit vs Population Size1')
plt.show()

# 画出cost的走势
plt.figure(figsize=(12, 8))
plt.xlabel('Iterations')
plt.ylabel('Cost')
plt.title('Error vs Training Epoch')
plt.plot(np.arange(iters), cost, 'r')
plt.show()	

多变量线性回归

• 𝑛 代表特征的数量
• 𝑥 (𝑖)代表第 𝑖 个训练实例，是特征矩阵中的第𝑖行，是一个向量（vector）。
• 支持多变量的假设 ℎ 表示为：ℎ𝜃 (𝑥) = 𝜃0 + 𝜃1𝑥1 + 𝜃2𝑥2+. . . +𝜃𝑛𝑥𝑛，

这个公式中有𝑛 + 1个参数和𝑛个变量，为了使得公式能够简化一些，引入𝑥0 = 1，则公 式转化为：ℎ𝜃 (𝑥) = 𝜃0𝑥0 + 𝜃1𝑥1 + 𝜃2𝑥2+. . . +𝜃𝑛𝑥𝑛。

此时模型中的参数是一个𝑛 + 1维的向量，任何一个训练实例也都是𝑛 + 1维的向量，特 征矩阵𝑋的维度是 𝑚 ∗ (𝑛 + 1)。 因此公式可以简化为：ℎ𝜃 (𝑥) = 𝜃 𝑇𝑋，其中上标𝑇代表矩阵转置。

多变量梯度下降

特征缩放

在我们面对多维特征问题的时候，我们要保证这些特征都具有相近的尺度，这将帮助梯 度下降算法更快地收敛。

以房价问题为例，假设我们使用两个特征，房屋的尺寸和房间的数量，尺寸的值为 0- 2000 平方英尺，而房间数量的值则是 0-5，以两个参数分别为横纵坐标，绘制代价函数的等 高线图能，看出图像会显得很扁，梯度下降算法需要非常多次的迭代才能收敛。

解决的方法是尝试将所有特征的尺度都尽量缩放到-1 到 1 之间。

学习率

梯度下降算法收敛所需要的迭代次数根据模型的不同而不同，我们不能提前预知，我们 可以绘制迭代次数和代价函数的图表来观测算法在何时趋于收敛。

梯度下降算法的每次迭代受到学习率的影响，如果学习率𝑎过小，则达到收敛所需的迭 代次数会非常高；如果学习率𝑎过大，每次迭代可能不会减小代价函数，可能会越过局部最 小值导致无法收敛。

正规方程

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的： 𝜕 𝜕𝜃𝑗 𝐽(𝜃𝑗) = 0 。 假设我们的训练集特征矩阵为 𝑋（包含了 𝑥0 = 1）并且我们的训练集结果为向量 𝑦，则利 用正规方程解出向量 𝜃 = (𝑋 𝑇𝑋) −1𝑋 𝑇𝑦 。

上标 T 代表矩阵转置，上标-1 代表矩阵的逆。设矩阵𝐴 = 𝑋 𝑇𝑋，则：(𝑋 𝑇𝑋) −1 = 𝐴 −1

对于那些不可逆的矩阵（通常是因为特征之间不独立，如同时包含英尺为单位的尺 寸和米为单位的尺寸两个特征，也有可能是特征数量大于训练集的数量），正规方程方法是 不能用的。

梯度下降和正规方程比较：

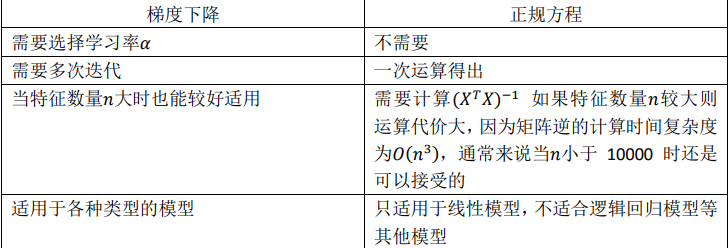
只要特征变量的数目并不大，标准方程是一个很好的计算参数𝜃的替代方法。 具体地说，只要特征变量数量小于一万，我通常使用标准方程法，而不使用梯度下降法。

随着学习算法越来越复杂，例如，分类算法，像逻辑回归算法， 我们会看到，实际上对于那些算法，并不能使用标准方程法。对于那些更复杂的学习算法， 我们将不得不仍然使用梯度下降法。因此，梯度下降法是一个非常有用的算法，可以用在有大量特征变量的线性回归问题。或者以后学到的其他的算法，因为标准方程法不适合或者不能用在它们上。但对于这个特定的线性回归模型，标准方程法是一个 比梯度下降法更快的替代算法。所以，根据具体的问题，以及你的特征变量的数量，这两种算法都是值得学习的。