01 数组_csdn数组排序-优快云博客

本文链接：https://blog.youkuaiyun.com/weixin_45859411/article/details/140080758

数组

1. 数组排序

01 冒泡排序

首先将数组想象是一排「泡泡」，元素值的大小与泡泡的大小成正比。
然后从左到右依次比较相邻的两个「泡泡」：
- 如果左侧泡泡大于右侧泡泡，则交换两个泡泡的位置。
- 如果左侧泡泡小于等于右侧泡泡，则两个泡泡保持不变。
这 1 趟遍历完成之后，最大的泡泡就会放置到所有泡泡的最右侧，就像是「泡泡」从水底向上浮到了水面。

def bubbleSort(nums):
    for i in range(0,len(nums)-1):
        flag = False
        for j in range(0,len(nums)-1-i):
            if nums[j]>nums[j+1]:
                #使用python的多重赋值来进行两个变量的数据交换
                nums[j],nums[j+1] = nums[j+1],nums[j]
                flag = True
            if not flag:
                break
    return nums
nums = [5,4,3,2,1]
print(bubbleSort(nums))

02 选择排序

将数组分为两个区间：左侧为已排序区间，右侧为未排序区间。每趟从未排序区间中选择一个值最小的元素，放到已排序区间的末尾，从而将该元素划分到已排序区间。

def selectionSort(nums):
    for i in range(len(nums)):
        min_index = i
        for j in range(i,len(nums)):
            if nums[min_index] > nums[j]:
                min_index = j
        if i != min_index:
            nums[i],nums[min_index] = nums[min_index],nums[i]
    return nums
nums = [5,4,3,2,1]
print(selectionSort(nums))

03 插入排序

将数组分为两个区间：左侧为有序区间，右侧为无序区间。每趟从无序区间取出一个元素，然后将其插入到有序区间的适当位置。

注意：从第二个元素开始遍历

def insertionSort(nums):
    for i in range(1,len(nums)):
        temp =  nums[i]
        for j in range(i,-1,-1):   #小技巧：这里使用range则j不会像c++的for(j = i;j >0;j--) 循环一样，循环结束后会到0，因此就让range再向后取一位。
            if nums[j-1] > temp:
                nums[j] = nums[j-1]
            else:
                break
        nums[j] = temp
    return nums
print(insertionSort([5,2,3,1,6,4]))

#第二种写法
def insertionSort2(nums):
    for i in range(1,len(nums)):
        temp = nums[i]
        j = i
        while j > 0 and nums[j-1] > temp:
            nums[j] = nums[j-1]
            j -= 1
        nums[j] = temp
    return nums
print(insertionSort2([5,2,3,1,6,4]))

04 希尔排序

基本思想：将整个数组切按照一定的间隔取值划分为若干个子数组，每个子数组分别进行插入排序。然后逐渐缩小间隔进行下一轮划分子数组和对子数组进行插入排序。直至最后一轮排序间隔为1，对整个数组进行插入排序

def shellSort(nums):
    gap = len(nums)//2
    while gap > 0:
        i = gap
        while i < len(nums):
            temp = nums[i]
            j = i
            while j > 0 and nums[j-gap] > temp:
                nums[j] = nums[j-gap]
                j -= gap
            nums[j] = temp
            i += 1
        gap -= 1
    return nums

print(shellSort([5,2,3,1,6,4]))

05. 归并排序

基本思想：采用经典的分治策略，先递归地将当前数组平均分成两半，然后将有序数组两两合并，最终合并成一个有序数组。

def merge(left_nums, right_nums):
    left_i = 0
    right_i = 0
    nums = []

    while left_i < len(left_nums) and right_i < len(right_nums):
        if left_nums[left_i] > right_nums[right_i]:
            nums.append(right_nums[right_i])
            right_i += 1
        else:
            nums.append(left_nums[left_i])
            left_i += 1

    while left_i < len(left_nums):
        nums.append(left_nums[left_i])
        left_i += 1
    while right_i < len(right_nums):
        nums.append(right_nums[right_i])
        right_i += 1
    return nums

def mergeSort(nums):
    if len(nums) <= 1:
        return nums
    mid = len(nums)//2
    #先将左右两个序列分别进行排序
    left_nums = mergeSort(nums[:mid])
    right_nums = mergeSort(nums[mid:])
    #将两个排好序的序列序列进行合并
    return merge(left_nums,right_nums)

print(mergeSort([5,2,3,1,6,4]))

06 快速排序

基本思想：采用经典的分治策略，选择数组中某个元素作为基准数，通过一趟排序将数组分为独立的两个子数组，一个子数组中所有元素值都比基准数小，另一个子数组中所有元素值都比基准数大。然后再按照同样的方式递归的对两个子数组分别进行快速排序，以达到整个数组有序。

每轮确定一个数字的位置

def partition(nums,low,height):
    #以首个元素作为基数，将元素进行左右划分
    temp= nums[low]
    left,right = low,height
    
    while left<right:
        while nums[right] >= temp and left<right: 
            right -= 1
        nums[left] = nums[right]
        
        while nums[left] <= temp and left<right: 
            left += 1
        nums[right] = nums[left]
    nums[left] = temp
    #返回基数的位置
    return left

def quickSort(nums,low,height):
    if low < height:
        #首先划分两个数组
        #划分数组：寻找一个基数，基数的左边为小于该数的值，右边为大于该数的值
        pivot = partition(nums,low,height)
        #接着对划分好的数组进行快速排序
        quickSort(nums,low,pivot-1)
        quickSort(nums,pivot+1,height)
    return nums

nums = [5,2,3,1,6,4]
print(quickSort(nums,0,len(nums)-1))

07 堆排序

堆的定义

堆顶元素

就是首个元素

向堆中插入元素

将新元素插入堆的末尾，也就是存储堆的数组的末尾
从新插入的节点开始，将插入节点与其父节点进行比较，若不满足特性则与父节点进行交换
重复上述步骤直至新节点不再大于其父节点，或者到达了堆的根节点

def push(max_heap,val):
    max_heap.append(val)
    size = len(max_heap)
    shift_heap(max_heap,size-1)
    return max_heap
#新插入节点，向上找到自己的位置 
def shift_heap(max_heap,point):
    i = point
    while i > 0:
        if max_heap[i] > max_heap[(i-1) // 2]:
            max_heap[i],max_heap[(i-1)//2] = max_heap[(i-1)//2],max_heap[i]
            i = (i-1)//2
        else:
            break
max_heap=[9,8,5,1,2,3]
print(push(max_heap,14))

堆父子节点的坐标关系：
父节点为i，子节点为left_j,right_j
left_j = 2 * i + 1
right_j = 2 * i + 2

i = (j-1) // 2

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

删除堆顶元素

将堆顶元素与堆的末尾元素进行交换
移除堆尾元素
从新的堆顶元素开始，将其与其较大的子节点进行比较和交换，将对顶元素下沉到合适的位置
重复上述步骤，知道新的堆顶元素不再小于其子节点，或者到达了底部

def remove(max_heap):
    size = len(max_heap)
    max_heap[0],max_heap[-1] = max_heap[-1],max_heap[0]
    #删除一个元素后，max_heap的元素数量少1,
    shift_heap(max_heap,size-1)
    return max_heap

#删除栈顶元素，最后一个元素被换到栈顶的位置，从上向下找到该元素的位置
def shift_heap(max_heap,size):
   i = 0
   j= 2*i+1 
   temp = max_heap[0]
   while j < size:
       #将栈顶元素与子节点中的最大元素进行比较，如果比栈顶元素大那么就交换
       if max_heap[j] < max_heap[j+1] and j+1 < size: j += 1
       if max_heap[j] > max_heap[i]:
           max_heap[i] = max_heap[j] 
           i = j
       else:
            max_heap[i] = temp
            break 
       j= 2*i+1 
   max_heap.pop()

max_heap = [9,8,5,1,2,3]
print(remove(max_heap))

堆排序

算法思想：借用「堆结构」所设计的排序算法。将数组转化为大顶堆，重复从大顶堆中取出数值最大的节点（取出栈顶元素），并让剩余的堆结构继续维持大顶堆性质

堆排序的算法步骤

构建初始大顶堆
交换元素调整堆
重复交换和调整堆

def push(nums):
    max_heap = []
    size = len(nums)
    for i in range(size):
        if i == 0:
            max_heap.append(nums[i])
        else:
            max_heap.append(nums[i])
            j = i
            #将插入的元素位置进行调整
            while j > 0:
                if max_heap[(j-1)//2] < max_heap[j]:
                    max_heap[(j-1)//2],max_heap[j] = max_heap[j],max_heap[(j-1)//2]
                    j = (j-1)//2
                else:
                    break
    return max_heap

def shift_heap(max_heap,size):
    i = 0
    j = 2*i + 1
    temp = max_heap[0]
    
    while j < size:
        if max_heap[j] < max_heap[j+1] and j+1 < size:
            j += 1
        if max_heap[i] < max_heap[j]:
            max_heap[i] = max_heap[j]
            i = j
            j = 2*i + 1
        else:
            break
    max_heap[i] = temp
                
    
def heapSort(nums):
    #构建初始大根堆
    max_heap = push(nums)
    print("初始大根堆:",max_heap)
    size = len(nums)
    
    #依次输出堆顶元素
    for i in range(size):
        print("堆顶元素：",max_heap[0])
        #将堆顶元素与最后一个元素进行交换
        max_heap[0],max_heap[size-i-1] = max_heap[size-i-1],max_heap[0]
        #调整新的堆
        shift_heap(max_heap,size-1-i)
        
nums = [1,2,3,5,8,9]
print(heapSort(nums))

2. 数组的二分查找

简单的二分查找（模板）记住即可

def search(self, nums, target):
        """
        :type nums: List[int]
        :type target: int
        :rtype: int
        """
        left,right = 0,len(nums)-1
        while left <= right:
            mid = left + (right - left)//2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        return -1

二分查找的细节问题

区间开闭问题
区间应该是[left,right]还是(left,right]
- 实际解题中建议全部使用[left,right]
mid取值问题
mid = (left+right)//2 还是 mid = (left + right + 1)//2

当待查找区间中的元素个数为偶数时，使用 mid = (left + right) // 2 式子我们能取到中间靠左边元素的下标位置，使用 mid = (left + right + 1) // 2 式子我们能取到中间靠右边元素的下标位置。
而对于这两个取值公式，大多数时候是选择第一个公式。不过，有些情况下，是需要考虑第二个公式的，
出界条件的判断
left <= right 还是 left< right

如果判断语句为 left <= right，并且查找的元素不在有序数组中，则while语句的出界条件是left > right,也就是left == right+1，写成区间形式就是[right+1,right],此时待查区间为空，待查区间中没有元素的存在，此时终止循环可以返回-1
当判断语句为left < right 时，出界条件为left == right 也就是区间为[left,right]此时区间中还有一个元素没有被判断。
比如说[2,2]如果元素Nums[2]刚好就是目标元素target，此时终止循环，返回-1就漏掉了这个元素
- 但是如果我们还是想要使用 left < right 的话，怎么办？
  可以在出界之后增加一层判断，判断 left 所指向位置是否等于目标元素，如果是的话就返回 left，如果不是的话返回 −1
搜索范围的选择，有三种写法：
- left = mid + 1 、right = mid -1
- left = mid、right = mid
- left = mid, right = mid -1
  我们到底应该如何确定搜索区间范围呢？
  这是二分查找的一个难点，写错了很容易造成死循环，或者得不到正确结果。这其实跟二分查找算法的两种不同思路和三种写法有关。
思路 1：「直接法」—— 在循环体中找到元素后直接返回结果。

思路 2：「排除法」—— 在循环体中排除目标元素一定不存在区间，判断最后区间中剩余的一个元素是否为目标元素
- 取两个节点中心位置 mid，比较目标元素和中间元素的大小，先将目标元素一定不存在的区间排除。
- 然后在剩余区间继续查找元素，继续根据条件排除目标元素一定不存在的区间。
- 直到区间中只剩下最后一个元素，然后再判断这个元素是否是目标元素。

# 思路1不再做解释，看模板代码即可
#下面对思路2进行解释
#代码1： 
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        # 在区间 [left, right] 内查找 target
        #   这里空间循环后区间中会剩余一个元素，在循环外对该元素做单独的判断
        while left < right:
            # 取区间中间节点
            
            mid = left + (right - left) // 2
            # nums[mid] 小于目标值，排除掉不可能区间 [left, mid]，在 [mid + 1, right] 中继续搜索
            if nums[mid] < target:
                left = mid + 1 
            # nums[mid] 大于等于目标值，目标元素可能在 [left, mid] 中，在 [left, mid] 中继续搜索
            else:
                right = mid
        # 判断区间剩余元素是否为目标元素，不是则返回 -1
        return left if nums[left] == target else -1
#代码2
class Solution:
    def search(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        
        # 在区间 [left, right] 内查找 target
        while left < right:
            # 取区间中间节点，这里采用向上取整的方式
            """
            如果mid = (left+right) // 2
            那么当 right = left + 1，即两个边界相邻时，mid = left，right = right
            当区间取[mid,right]时就会陷入死循环
            将该式子与else的注释联系起来就理解了 
            """ 
            mid = left + (right - left + 1) // 2
            # nums[mid] 大于目标值，排除掉不可能区间 [mid, right]，在 [left, mid - 1] 中继续搜索
            if nums[mid] > target:
                right = mid - 1 
            # nums[mid] 小于等于目标值，目标元素可能在 [mid, right] 中，在 [mid, right] 中继续搜索
            else:
                left = mid
        # 判断区间剩余元素是否为目标元素，不是则返回 -1
        return left if nums[left] == target else -1

3. 双指针

双指针（Two Pointers）简介：
指的是在遍历元素的过程中，不是使用单个指针进行访问，而是使用两个指针进行访问，从而达到相应的目的。如果两个指针方向相反，则称为「对撞指针」。如果两个指针方向相同，则称为「快慢指针」。如果两个指针分别属于不同的数组 \ 链表，则称为「分离双指针」。

在数组的区间问题上，暴力算法的时间复杂度往往是O(n2) 而双指针利用了区间「单调性」的性质，可以将时间复杂度降到O(n)
对撞指针：
指的是两个指针 left、right 分别指向序列第一个元素和最后一个元素，然后 left 指针不断递增，right 不断递减，直到两个指针的值相撞（left==right），或者满足其他要求的特殊条件为止。步骤：
- 使用两个指针 left，right。left 指向序列第一个元素，即：left=0，right 指向序列最后一个元素，即：right=len(nums)−1。
- 在循环体中将左右指针相向移动，当满足一定条件时，将左指针右移left+=1。当满足另外一定条件时，将右指针左移，right−=1。
  -直到两指针相撞（即 left==right），或者满足其他要求的特殊条件时，跳出循环体。
快慢指针
指的是两个指针从同一侧开始遍历序列，且移动的步长一个快一个慢。移动快的指针被称为「快指针（fast）」，移动慢的指针被称为「慢指针（slow）」。两个指针以不同速度、不同策略移动，直到快指针移动到数组尾端，或者两指针相交，或者满足其他特殊条件停止

适合解决数组中的移动、删除元素问题，或者链表中的判断是否有环、长度问题。

步骤：
1. 使用两个指针 slow、fast。slow 一般指向序列第一个元素，即:slow =0，fast 一般指向序列第二个元素，即:fast =1。
2. 在循环体中将左右指针向右移动。当满足一定条件时，将慢指针右移，即 slow+=1。当满足另外一定条件时(也可能不需要满足条件)，将快指针右移，即fast+=1。
3. 到快指针移动到数组尾端(即 fast == len(nums)-1)，或者两指针相交，或者满足其他特殊条件时跳出循环体。

#快慢指针的模板
slow = 0
fast = 1
while 没有遍历完：
    if 满足要求的特殊条件:
        slow += 1
    fast += 1
return 合适的值

分离双指针
两个指针分别属于不同的数组，两个指针分别在两个数组中移动。
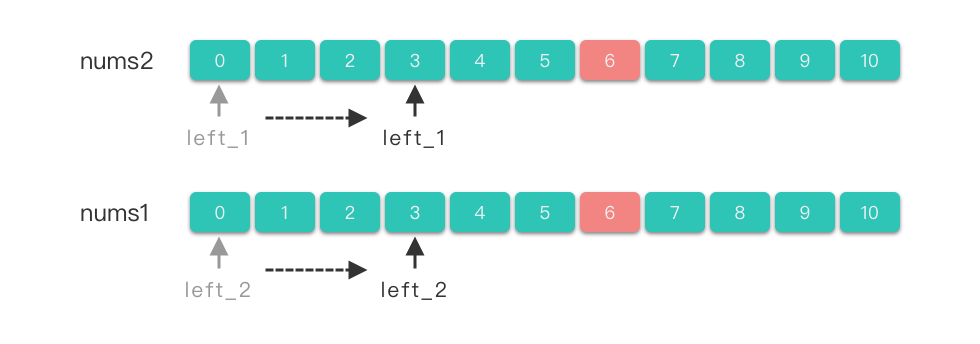
- 步骤：
  1. 使用两个指针 left 1、left 2。left 1指向第一个数组的第一个元素，即:left 1=0，left_2指向第二个数组的第一个元素，即:le.ft 2 =0。
  2. 当满足一定条件时，两个指针同时右移，即 left_1 += 1、left_2 += 1。
  3. 当满足另外一定条件时，将 left_1指针右移，即 left_1 += 1。
  4. 当满足其他一定条件时，将 left_2 指针右移，即 left_2 += 1.
  5. 当其中一个数组遍历完时或者满足其他特殊条件时跳出循环体。
- 使用范围：
  分离双指针一般用于处理有序数组合并，求交集、并集问题。

#模板
left_1 = 0
left_2 = 0

while left_1 < len(nums1) and left_2 < len(nums2):
    if 一定条件 1:
        left_1 += 1
        left_2 += 1
    elif 一定条件 2:
        left_1 += 1
    elif 一定条件 3:
        left_2 += 1

4. 滑动窗口

滑动窗口算法：在给定数组 / 字符串上维护一个固定长度或不定长度的窗口。可以对窗口进行滑动操作、缩放操作，以及维护最优解操作。

滑动操作：窗口可按照一定方向进行移动。最常见的是向右侧移动
缩放操作：对于不定长度的窗口，可以从左侧缩小窗口长度，也可以从右侧增大窗口长度

可以将滑动窗口看做是快慢指针的一种特殊形式

外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

适用范围:解决一些查找满足一定条件的连续区间的性质（长度等）的问题。该算法可以将一部分问题中的嵌套循环转变为一个单循环，因此它可以减少时间复杂度。按照窗口长度的固定情况，我们可以将滑动窗口题目分为以下两种：
1. 固定长度窗口

算法步骤：假设窗口的固定大小为window_size

- 使用两个指针：left、right。 初始时，两个指针都指向同一个元素，即：left = 0,right = 0,区间[left,right]被称为一个窗口
- 当窗口未达到window_size，的时候就right向右移动，先将窗口内的元素数量达到window_size，window.append(nums[right])
- 当窗口达到window_size的时候即：right-left+1 >= window_size
  - 如果满足，再根据要求求最优解
  - 然后left向右移动缩小窗口，使得窗口大小时钟保持window_size
- 向右移动right，将元素填入窗口中

直到right达到数组末尾

```python
left = 0

right = 0

while right < len(nums):

window.append(nums[right])

  #超过窗口大小时，缩小窗口，维护窗口中始终为 window_size 的长度
  if right - left + 1 >= window_size:
    #维护答案
    window.popleft()
 left += 1

  right += 1
```

2. 不定长度窗口

算法步骤：
- left = 0,right = 0.left,right都指向序列的第一个元素
- 将区间最右侧的元素添加入窗口，windows.append(nums[right])
- 向右移动right指针，直到窗口中的连续元素满足要求。
- 停止增加窗口大小，不断将左侧元素溢出窗口。windows.popleft(nums[left])
- 向右移动left，从而缩小窗口长度，直到窗口中的连续元素不再满足要求
- 直到right到达序列末尾，结束

#不定长度窗口模板
left = 0
right = 0

while right < len(nums):
  window.append(nums[right])
    
  while 窗口需要缩小:
    # ... 可维护答案
    window.popleft()
    left += 1
    

    #若是求最小满足条件则这里添加一个最小满足条件的判断

    # 向右侧增大窗口
  right += 1

两种题型：
- 求解最大的满足条件的窗口
- 求解最小的满足条件的窗口

最大的满足条件的窗口：无重复字符的最长子串

 def lengthOfLongestSubstring(self, s):
        """
        :type s: str
        :rtype: int
        """
        left,right = 0,0
        windows = []
        length = 0
        max_length = 0
        while right < len(s):
            windows.append(s[right])
            length += 1
            while windows.count(s[right]) > 1:
                left += 1
                length -= 1
                del windows[0]
            
            if length > max_length: max_length = length

            right += 1
        return max_length

最小的满足条件的窗口：长度最小的子数组

 def minSubArrayLen(self, target, nums):
        """
        :type target: int
        :type nums: List[int]
        :rtype: int
        """
        right,left = 0,0
        sum_nums = 0
        length = 0
        min_length = 999999999999
        k = 0
        flag = 0

        while right < len(nums):
            sum_nums += nums[right]

            while sum_nums >= target:
                sum_nums -= nums[left]
                k = nums[left]
                length -= 1
                left += 1

            if sum_nums + k >= target and min_length > right-left+2:
                min_length = right-left+2
                flag = 1

            right += 1
            
        if flag == 1: 
            return min_length
        else: return 0

乘积小于 K 的子数组

left = 0
right = 0
count = 0
mul = 1

while right < len(nums):
    mul *= nums[right]
    while mul >= k and left <= right:
        mul = mul // nums[left]
        left += 1
    count += right - left + 1
    right += 1
return count


"""
!!!!!!!!注意：以右端点元素为末尾元素的子数组的个数 end-start+1
"""

um_nums + k >= target and min_length > right-left+2:
min_length = right-left+2
flag = 1

        right += 1
        
    if flag == 1: 
        return min_length
    else: return 0


[乘积小于 K 的子数组
](https://leetcode.cn/problems/subarray-product-less-than-k/)


```python
left = 0
right = 0
count = 0
mul = 1

while right < len(nums):
    mul *= nums[right]
    while mul >= k and left <= right:
        mul = mul // nums[left]
        left += 1
    count += right - left + 1
    right += 1
return count


"""
!!!!!!!!注意：以右端点元素为末尾元素的子数组的个数 end-start+1
"""