力扣日记:【回溯算法篇】47. 全排列 II
日期:2023.2.22
参考:代码随想录、力扣
47. 全排列 II
题目描述
难度:中等
给定一个可包含重复数字的序列 nums ,按任意顺序 返回所有不重复的全排列。
示例 1:
输入:nums = [1,1,2]
输出:
[[1,1,2],
[1,2,1],
[2,1,1]]
示例 2:
输入:nums = [1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
提示:
- 1 <= nums.length <= 8
- -10 <= nums[i] <= 10
题解
cppver
class Solution {
public:
#define SOLUTION 2
vector<int> path;
vector<vector<int>> result;
vector<vector<int>> permuteUnique(vector<int>& nums) {
// 排序
sort(nums.begin(), nums.end());
vector<bool> used(nums.size(), false);
backtracking(nums, used);
return result;
}
#if SOLUTION == 1
void backtracking(vector<int>& nums, vector<bool>& used) { // 因为存在重复值,所以不宜用哈希表记录是否使用过
// 终止条件
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
int lastNum = -11;
// for 横向遍历
for (int i = 0; i < nums.size(); i++) {
// 需要标记哪些值已经取过了 used[i]
if (used[i] == true) continue; // 取过了,则跳过该值
// 去重
if (nums[i] == lastNum) continue; // 与for循环的上一次取值重复
// 否则,标记取过,并进行取值与递归
lastNum = nums[i]; // 更新 lastNum
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
#elif SOLUTION == 2
void backtracking(vector<int>& nums, vector<bool>& used) { // 因为存在重复值,所以不宜用哈希表记录是否使用过
// 终止条件
if (path.size() == nums.size()) {
result.push_back(path);
return;
}
// 使用 nums[i] == nums[i-1] 结合 used[i-1] 来判断是树枝重复还是树层重复
// 树层重复的条件为:i > 0 && nums[i] == nums[i-1] && used[i-1] == false (上一个位置的元素未使用,说明是树层)
// 树枝重复的条件为:i > 0 && nums[i] == nums[i-1] && used[i-1] == true
// for 横向遍历
for (int i = 0; i < nums.size(); i++) {
// 树枝(纵向递归):标记哪些值已经取过了 used[i]
if (used[i] == true) continue; // 取过了,则跳过该值
// 树层(用于去重)
if (i > 0 && nums[i] == nums[i-1] && used[i-1] == false) continue; // 与for循环的上一次取值重复
// 否则,标记取过,并进行取值与递归
used[i] = true;
path.push_back(nums[i]);
backtracking(nums, used);
path.pop_back();
used[i] = false;
}
}
#endif
};
复杂度
- 时间复杂度: O(n! * n)
- 空间复杂度: O(n)
思路总结
- 本题与 46. 全排列 的区别在于,集合中可能存在重复元素。因此,需要考虑去重,即在46题的基础上,需要在for循环遍历(横向遍历)中,过滤掉相同的元素(但又不能影响到纵向递归时元素的可重复选取)。
- 不同于 40.组合总和 II 和 90.子集 II,全排列在for循环遍历时不能使用
startindex,即每次for循环遍历都会从头开始遍历,不能直接在for循环中,用if (i > 0 && nums[i] == nums[i-1]) continue;来跳过重复元素,因为这样会使得在纵向递归时也无法选取到重复元素。 - 因此,需要一个只会影响到横向遍历的变量,即代码中在for循环前定义的
lastNum(这样每次for循环前会重置lastNum),用来记录相同层中for循环上次取到的元素——如果当前值与for循环上次取到的值相同,则跳过当前元素。且只有在该值也满足“纵向递归中当前位置未取过”的条件(used[i] == false)才会更新该lastNum(即当前值能进行取值、递归才会更新)。 - 注意:
- 去重 要提前做好排序。
- 由于本题存在重复元素,所以不能使用按值大小记录是否取过的哈希表作为
used,而要使用按位置记录的used(vector<bool> used(nums.size(), false))。 - 去重与是否使用过的if-continue判断条件的前后位置不影响(也可以写在一起),但取值、更新、递归、回溯等(所谓处理节点)一定要放在两者后面。
- 树形结构示意图:
- 代码随想录版本:
- 使用
nums[i] == nums[i-1]结合used[i-1]来判断是树枝重复还是树层重复- 树层重复的条件为:
i > 0 && nums[i] == nums[i-1] && used[i-1] == false(上一个位置的元素未使用,说明是树层) - 树枝重复的条件为:
i > 0 && nums[i] == nums[i-1] && used[i-1] == true - 如图
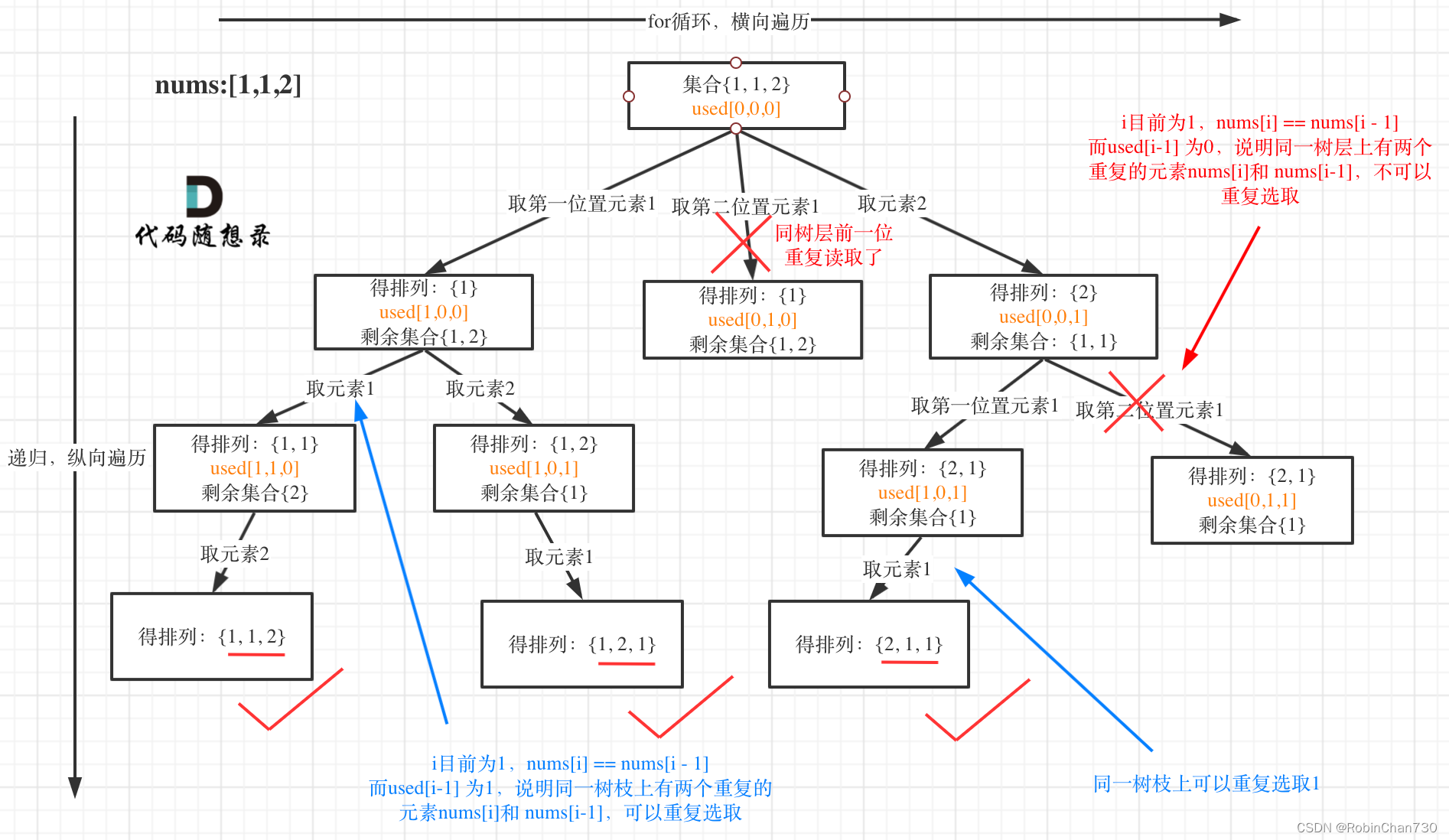
- 树层重复的条件为:
- 所以在for循环中
- 第一个条件用于排列取值
// 树枝(纵向递归):标记哪些值已经取过了 used[i] if (used[i] == true) continue; // 取过了,则跳过该值 - 第二个条件用于树枝去重
if (i > 0 && nums[i] == nums[i-1] && used[i-1] == false) continue;
- 第一个条件用于排列取值
- 使用




 本文详细介绍了如何解决LeetCode47.全排列II的问题,重点在于处理包含重复元素的全排列去重,使用了backtracking算法和vector数据结构,并区分了树层重复和树枝重复的判断条件。
本文详细介绍了如何解决LeetCode47.全排列II的问题,重点在于处理包含重复元素的全排列去重,使用了backtracking算法和vector数据结构,并区分了树层重复和树枝重复的判断条件。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








