力扣日记1.26-【回溯算法篇】40. 组合总和 II

最新推荐文章于 2025-12-26 16:25:00 发布

原创最新推荐文章于 2025-12-26 16:25:00 发布 · 1.1k 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #leetcode #职场和发展

本文解析了如何使用回溯算法解决LeetCode的组合总和II问题，重点讨论了如何通过去重优化，确保每个组合中的数字只使用一次，避免重复组合。通过递归实现并结合剪枝策略，有效降低空间复杂度。

力扣日记：【回溯算法篇】40. 组合总和 II

日期：2023.1.23
参考：代码随想录、力扣

40. 组合总和 II

题目描述

难度：中等

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

注意：解集不能包含重复的组合。

示例 1:

输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]

示例 2:

输入: candidates = [2,5,2,1,2], target = 5,
输出:
[
[1,2,2],
[5]
]

提示:

1 <= candidates.length <= 100
1 <= candidates[i] <= 50
1 <= target <= 30

题解

class Solution {
public:
    vector<vector<int>> results;
    vector<int> path;
    int last_value = 0;
    vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
        sort(candidates.begin(), candidates.end());
        backtracking(candidates, target, 0, 0);
        return results;
    }
    void backtracking(vector<int>& candidates, int target, int startindex, int sum) {
        // 终止条件
        if (sum == target) {
            results.push_back(path);
            return;
        }
        // 每次for遍历前要重置last_value
        last_value = 0;
        for (int i = startindex; i < candidates.size() && sum + candidates[i] <= target; i++) { // 包含了剪枝优化
            // 去重操作
            if (candidates[i] == last_value) {
                // candidates[i] >= 1，如果当前取的值与上次弹出的值一样，则跳过，避免重复
                continue;   // 不能是break，因为后面可能有不重复的值也满足条件，也不能写到for条件中，因为一旦不满足则不会继续遍历
            }
            // 处理节点
            path.push_back(candidates[i]);
            // 递归
            backtracking(candidates, target, i + 1, sum + candidates[i]);
            path.pop_back();
            last_value = candidates[i]; // 更新last_value
        }
    }
};

复杂度

时间复杂度：
空间复杂度：

思路总结

本题关键在于去重
最开始仅考虑题目中 每个数字在每个组合只能使用一次，就只是通过对candidates排序以及startindex = i + 1来满足条件。忽略了candidates存在重复元素，这样会导致解集存在重复的组合。
- 如对示例2，如果不用去重操作，会使得结果包含多个[1,2,2]，如图所示：
  
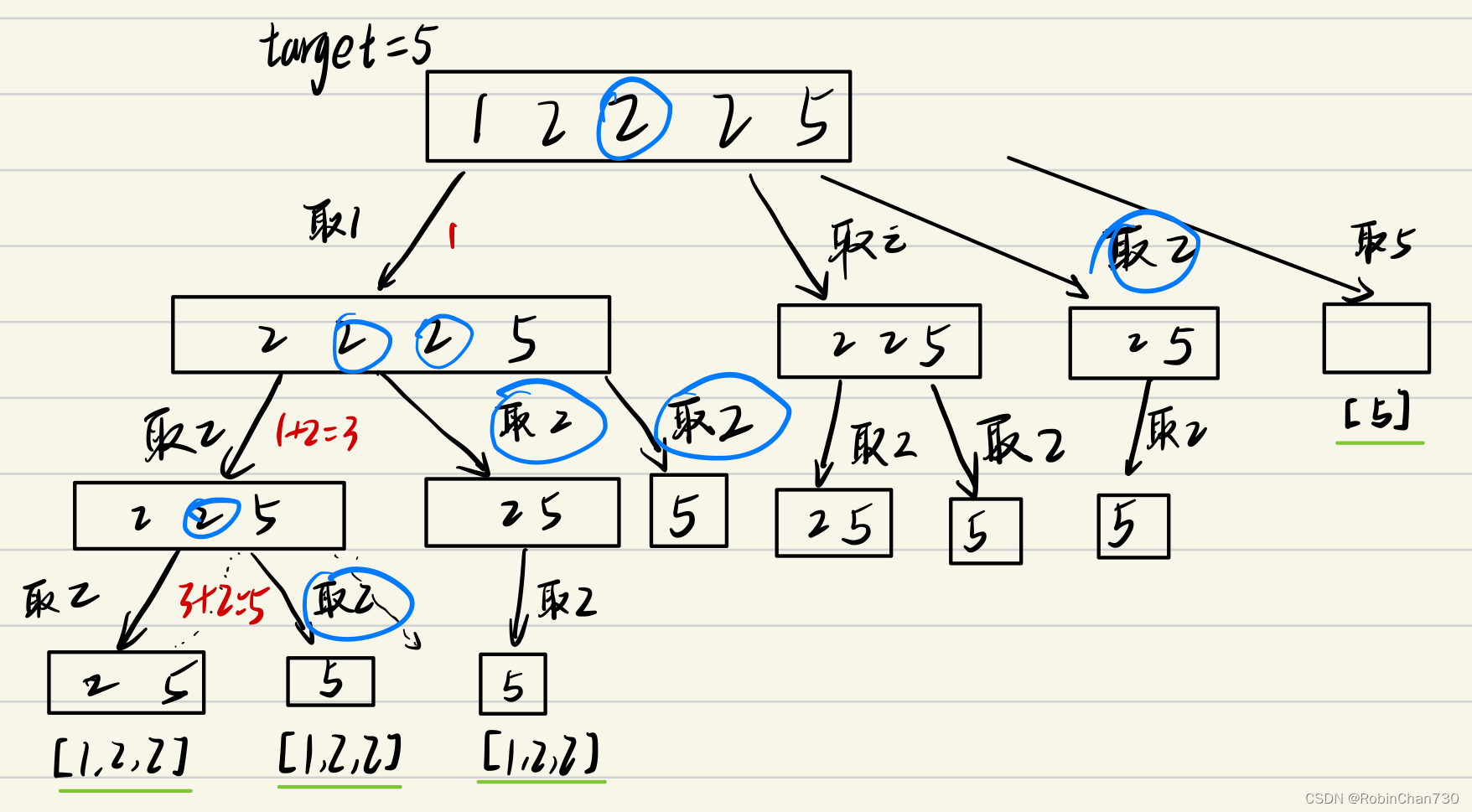
  其中蓝色圈出的2即为重复取当前集合的相同值导致的结果集重复（或无效的重复操作）
  观察可知，如果在每一层for循环的每一次取值，判断获得的值与上一次取的值last_value一样，则跳过本次取值，则可以避免这种情况，即
```
if (candidates[i] == last_value) {
	// candidates[i] >= 1，如果当前取的值与上次弹出的值一样，则跳过，避免重复
    continue;
}
```
  - 但要注意这里比较上一次取值，必须是在同一层循环（同一个for循环），所以每层for循环前都要重置last_value=0
  - 同时continue也不能是break，因为后面可能有不重复的值也满足条件，也不能写到for条件中，因为这样一旦不满足条件则会结束for循环
  - 代码随想录的操作是，通过条件i > startindex && candidates[i] == candidates[i - 1]来判断，则可以避免对for循环起始值的判断，本质也是同理
注意，去重前一定要先对数组进行排序
如果把所有组合求出来，再用set或者map去重，这么做很容易超时！所以要在搜索的过程中就进行去重。
代码随想录中关于“树枝去重”和“树层去重”的区别可以帮助理解“去重”。

所谓去重，其实就是使用过的元素不能重复选取。
组合问题可以抽象为树形结构，那么“使用过”在这个树形结构上是有两个维度的，一个维度是同一树枝上使用过，一个维度是同一树层上使用过。
回看一下题目，元素在同一个组合内是可以重复的，怎么重复都没事，但两个组合不能相同。
所以我们要去重的是同一树层上的“使用过”(for循环时要去重），同一树枝上的都是一个组合里的元素，不用去重。
……
强调一下，树层去重的话，需要对数组排序！

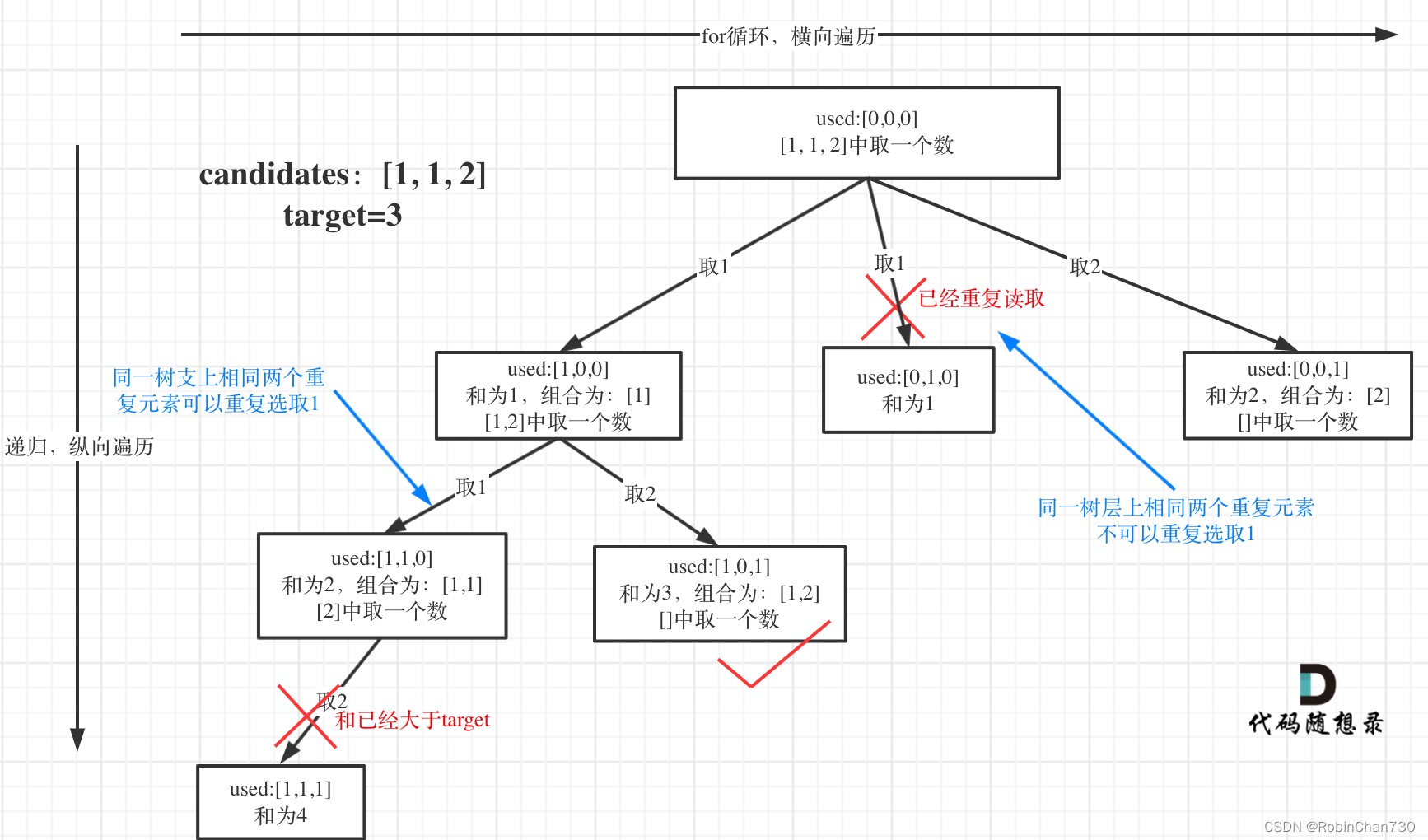
注：这里的used数组没有理解（），不用到也可以