目录
一. 基本概念
1.灰度直方图的定义
数字图像中各级灰度级与其出现的频数间的统计关系,可表示为:

且:

其中,k为图像的第k级灰度值,是中灰度值为k的像素个数;
n是图像的总像素个数;
L是灰度级数。
2.灰度直方图的性质
①直方图的位置缺失性;
②直方图与图像的一对多特性;
③直方图的可叠加性。
3.直方图与图像清晰性的关系
直方图反映了图像的清晰程度,当直方图均匀分布时,图像最清晰。
由此,我们可以利用直方图来达到使图像清晰的目的。
二.直方图均衡化
1.定义
通过原始图像的灰度非线性变换,使其直方图变成均匀分布,以增加图像灰度值的动态范围,从而达到增强图像整体对比度,使图像变清晰的效果。
2.图像灰度变换函数条件
①对0≤r≤1,s=T[r]是单调增函数;
②对0≤r≤1,0≤s=T[r]≤1。
同理,反变换r=T-1[s]应也满足单调增。
3.直方图均衡化的计算过程
①列出原始图像和变换后图像的灰度级:i,j=0,1,…,L-1,其中L是灰度级数;
②统计原图像各灰度级的像素个数ni;
③计算原始图像直方图:P(i)=ni / n,其中n为原始图像像素总个数;
④计算累积直方图:

⑤利用灰度变换函数计算变换后的灰度值,并四舍五入取整:

⑥确定灰度变换关系f(m,n)=i,据此将原图像的灰度值修正为:
g(m,n)=j;
⑦统计变换后各灰度级的像素个数nj;
⑧计算变换后图像的直方图:P(j)=nj / n
/*直方图均衡化*/
void Histogram_equalization(Mat& src, Mat& dst)
{
CV_Assert(src.depth() == CV_8U); //仅接受uchar图像
src.copyTo(dst);
int nr = src.rows;
int nc = src.cols;
int pixnum = nr * nc;
//灰度图像
if (src.channels() == 1)
{
//统计直方图
int gray[256] = { 0 };
for (int i = 1; i < nr; i++)
{
const uchar* ptr = src.ptr<uchar>(i);
for (int j = 0; j < nc; j++)
{
gray[ptr[j]]++;
}
}
//计算分布函数
int LUT[256];
int sum = 0;
for (int k = 0; k < 256; k++)
{
sum += gray[k];
LUT[k] = 255 * sum / pixnum;
}
//灰度变换(赋值)
for (int i = 1; i < nr; i++)
{
const uchar* ptr_src = src.ptr<uchar>(i);
uchar* ptr_dst = dst.ptr<uchar>(i);
for (int j = 0; j < nc; j++)
{
ptr_dst[j] = LUT[ptr_src[j]];
}
}
}
//彩色图像
else
{
//统计直方图
int B[256] = { 0 };
int G[256] = { 0 };
int R[256] = { 0 };
for (int i = 0; i < nr; i++)
{
for (int j = 0; j < nc; j++)
{
B[src.at<Vec3b>(i, j)[0]]++;
G[src.at<Vec3b>(i, j)[1]]++;
R[src.at<Vec3b>(i, j)[2]]++;
}
}
//计算分布函数
int LUT_B[256], LUT_G[256], LUT_R[256];
int sum_B = 0, sum_G = 0, sum_R = 0;
for (int k = 0; k < 256; k++)
{
sum_B += B[k];
sum_G += G[k];
sum_R += R[k];
LUT_B[k] = 255 * sum_B / pixnum;
LUT_G[k] = 255 * sum_G / pixnum;
LUT_R[k] = 255 * sum_R / pixnum;
}
//灰度变换
for (int i = 0; i < nr; i++)
{
for (int j = 0; j < nc; j++)
{
dst.at<Vec3b>(i, j)[0] = LUT_B[src.at<Vec3b>(i, j)[0]];
dst.at<Vec3b>(i, j)[1] = LUT_B[src.at<Vec3b>(i, j)[1]];
dst.at<Vec3b>(i, j)[2] = LUT_B[src.at<Vec3b>(i, j)[2]];
}
}
}
}

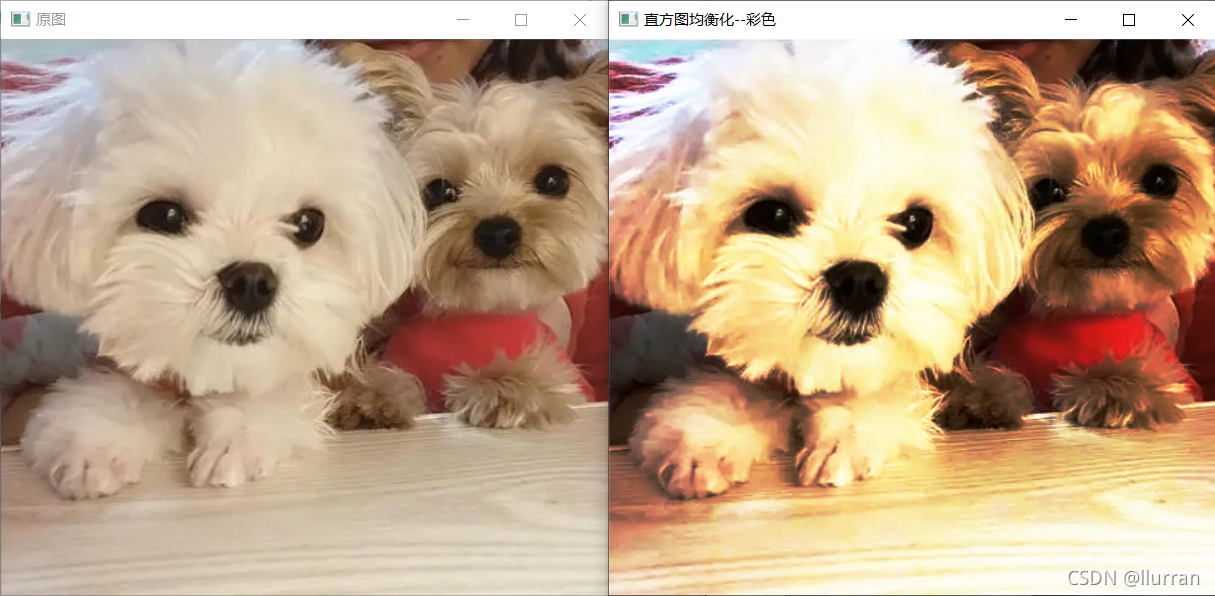
三.直方图规定化
1.定义
直方图均衡化能自动增强整个图像对比度,结果得到全局均匀化直方图,但实际应用中有时要求突出感兴趣灰度范围,即修正直方图使其具有要求的形式。

2.直方图规定化的步骤:
①对原直方图均衡化,即求其累积直方图P~i~: 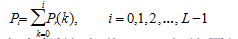 ②对规定直方图均衡化,即求其累计直方图P~j~: 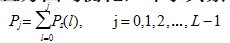 ③按 P~j~ --> P~i~ 最靠近的原则进行 i --> j 的变换; ④求出 i-->j 的变换函数,对原图像进行灰度变换 j=T[i]。 其中,P~r~(i)为原数字图像的直方图,P~r~(j)为规定直方图,i 和 j 分别为原图像和期望图像的灰度级,且具有相同的取值范围,即i,j=0,1,2,....,L-1。四.自适应直方图均衡化(AHE)
1.定义
AHE是一种用来改善图像对比度的图像处理技术,它与传统的直方图均衡化相比,不同点主要在于,AHE通过计算图像每一个显著区域的直方图,来重新分布图像的亮度值,因此它更适合用于来改善图像的局部对比度,以及增强图像边缘信息,利于分割。

2.缺点
AHE在增强对比度的同时会增强图像同质(均匀)区域的噪声,因此作为AHE的改进,CLAHE可以有效降低这种噪声的增强。
3.CLAHE
CLAHE与AHE最大的不同在于前者对对比度进行了限制,这一特性也可以被应用到全局的直方图均衡中,即Contrast Limited HE,简称CLHE,但实际中他很少被用到。
CLAHE中,每一个像素邻域都要进行对比度限制,从而得到对应的变换函数,被用来降低AHE中噪声的增强,这主要是通过限制AHE中的对比度增强来实现的。

























 1032
1032

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










