ADMM的运用主要在于处理含线性等式约束的优化问题,现在也被大量运用在深度学习等领域。其核心在于将原始的优化问题拆解成一些更好解决的子问题,进而解决最原始的优化问题。
基本模型
ADMM是通过对偶上升法推导延申的算法,最基础原始的问题是解决存在两个优化变量,并且只含等式约束的凸优化问题,其形式一般为:
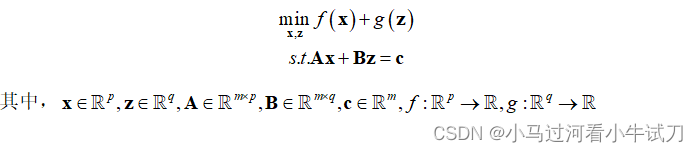
可通过拉格朗日乘数法将该问题转化为无条件极值问题,同时还进行了增广处理,得到增广拉格朗日函数:
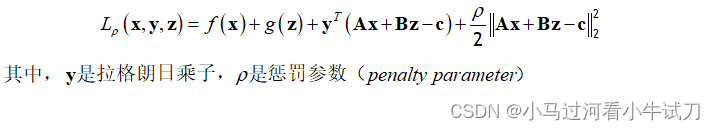
在这之后,通过固定其他变量,每次只更新其中一个变量的办法来拆解原问题,进行迭代计算,直至满足迭代停止条件完成求解:
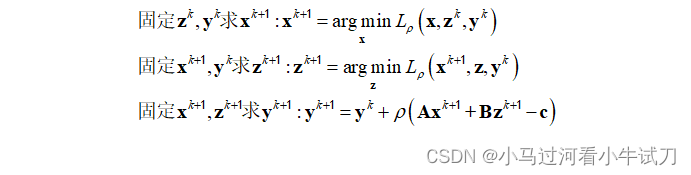
在此基础上可以进行一个缩放,令,以达到简化拉格朗日函数的效果:
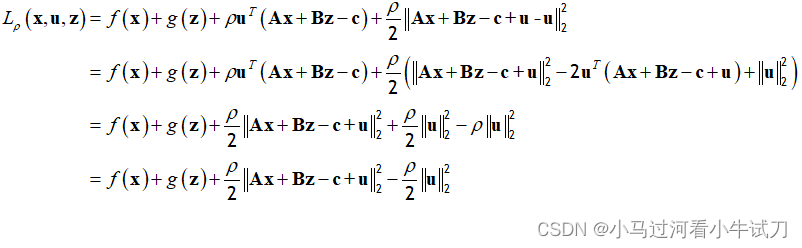
这时的更新也就简化了:
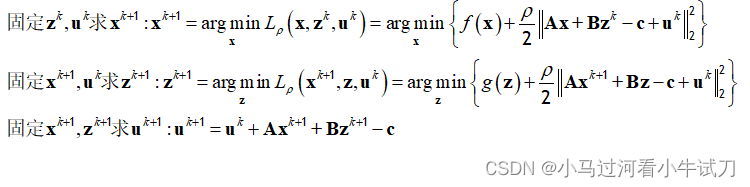








 ADMM(交替方向乘子法)主要用于解决含线性等式约束的优化问题,它通过拆解问题为可单独优化的子问题进行迭代求解。这一方法在深度学习领域有广泛应用,通过增广拉格朗日函数和交替更新变量的方式逐步逼近最优解。通过调整参数,可以简化更新步骤,提高求解效率。
ADMM(交替方向乘子法)主要用于解决含线性等式约束的优化问题,它通过拆解问题为可单独优化的子问题进行迭代求解。这一方法在深度学习领域有广泛应用,通过增广拉格朗日函数和交替更新变量的方式逐步逼近最优解。通过调整参数,可以简化更新步骤,提高求解效率。
















 3585
3585

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








