1.决策树的损失函数
在《统计学习方法》5.1.4决策树学习这一节中,书中有提到:决策树的损失函数通常是正则化的极大似然函数。
在决策树学习算法的过程中,为了尽可能正确分类训练样本,结点划分过程将不断重复,有时会造成决策树分支过多,这时就可能因为训练样本学得“太好”了,以至于把训练集自身的一些特点当作所有数据都具有的一般性质而导致过拟合。所以我们采用剪纸对其进行处理。
决策树的剪枝类似一种参数正则化的过程,其选择正则化的参数是树的叶子节点的个数。
设决策树
T
T
T的叶子节点个数为
∣
T
∣
|T|
∣T∣,
t
t
t 是树
T
T
T 的叶子节点,该叶节点有
N
t
N_t
Nt个样本点,其中
k
k
k类的样本点有
N
t
k
N_{tk}
Ntk个,
H
t
(
T
)
H_t(T)
Ht(T) 为叶节点
t
t
t上的经验熵,α⩾0 为正则化系数,则包含剪枝的决策树的损失函数可以定义为:
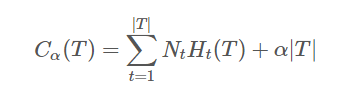
经验熵为:
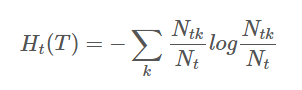
右边第一项表示误差大小,第二项表示模型的复杂度,也就是用叶节点表示,防止过拟化。
损失函数中的第一项表示模型对训练数据的预测误差,也就是模型的拟合程度,第二项表示模型的复杂程度,通过参数 α 控制二者的影响力。一旦 α 确定,那么我们只要选择损失函数最小的模型即可。
2.对决策树损失函数的理解
- 首先问一个问题,Ht(T)代表的是什么?你肯定会说是经验熵,那什么是经验熵,你肯定会说是不确定度,到这里都没错,那这个不确定度是什么的不确定度呢?
- 我的理解是,这个叶子节点内部取k个类的不确定度,注意是节点【内部】的不确定度,每个叶子节点可以看作是独立的,既然是内部的事情,凭什么暴力的将各个内部的不确定度相加,我们至少到同一个级别的平台再加吧。
- 不知道你现在有没有感觉暴力的相加确实少了点什么,我的理解是,少了该节点的样本数,也就是Nt。不知道你有没有注意到,信息熵只用到了概率,而忽略了样本数,也就是只关注内部各个类别的比例,而不在乎整体数量的多少,那么乘以Nt后,我们把它叫做不确定次数,不确定程度就是不确定次数归一化后的东西。
- 既然都这么暴力了,就更暴力一点,你把Ht(T)理解成频率,Nt*Ht(T)对应地理解成次数吧。比如有A股B股两支股票,A股买了10次,赚了7次,B股买了100次,赚了50次,赚的频率分别是0.7和0.5,那么计算你投资的能力,是0.7+0.5更有意义呢还是7+50更有意义呢?我觉得7+50更有意义吧。
虽然不确定性和不确定次数并非频率和次数,但它们的相对关系就这么理解吧。





















 2421
2421

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








