队列 广度优先搜索（BFS）

数据结构（先入先出FIFO）

自定义队列(循环队列)

class Queue {
    //存取数据的数组
    Object[] obj;

    //指向最后一次入队的位置
    int last = -1;

    //指向最后一次出队的位置
    int first = -1;

    //当前队列长度(目前想法是舍去该变量，实现循环队列)
    int count = 0;

    //队列可容纳元素长度,默认为10
    int number = 10;

    //构造
    public Queue() {
        this.obj = new Object[number];
    }

    public Queue(int number) {
        this.number = number;
        this.obj = new Object[number];
    }

    //入队
    boolean offer(Object e) {
        //当队列已满，不能入队
        if (count >= number) return false;
        //未满则入队
        //入队前先判断last是否在队列的边界
        if (last == number - 1) last = -1;
        obj[++last] = e;
        count++;
        return true;
    }

    //出队
    Object poll() {
        //判断队列是否为空
        if (count == 0) return null;
        //队列不空进行以下操作
        //判断first是否在队列的边界,若是则指向0
        if (first == number - 1) first = 0;
        else first++;
        count--;
        return obj[first];
    }

    //当前队列长度
    int size() {
        return count;
    }
}

广度优先搜索(BFS)：

思想：绝不深入探索，除非已经访问过当前层级的所有节点。

Queue<xxx> queue = new LinkedList<>();
queue.add(..);//入队：尾部插入
while(!queue.isEmpty()){
	int size = queue.size();
	for (int i = 0; i < size; ++i){
		xx = queue.poll();//出队：头部取出
		...
		if(...) queue.add(...);//添加其子节点入队
	}
	//若是解决最短路径等相关问题，需添加步长变量
	count++;
}

模型

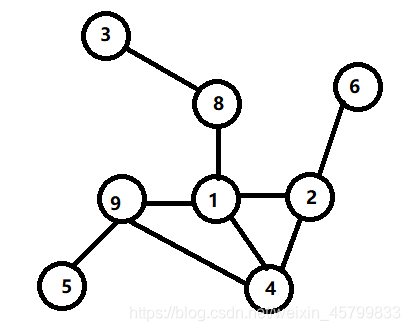
推导

依据代码及模型进行分析：(解决节点8到节点4的最短路径)

1. 将节点8入队
2. 进入while循环，条件：队列不空（队列为空，意味着已遍历所有节点）
3. 获取当前队列长度，进行for循环，循环次数即队列长度
4. 通过循环将队列元素从头部取出，暂命名为X
5. 通过X判断其是否为我们需要的节点4{ false：将其子节点入队，即其相邻节点（3，9，1，2） true：返回步长}
6. 当for循环结束，意味着旧队列里不存在要找的节点，则步长+1，且当前队列为【3，9，1，2】
7. 重复以上流程，直到找到节点4，并返回步长，或者队列为空，结束循环，表示没有该节点。
8. 以上推导存在bug，即其将会陷入闭环，队列永远不会为空，当我们要找的节点存在则会造成重复查找以致效率低下，若不存在，则程序永远不会出结果。

优化

思想：以空间换时间

• 推荐使用Set集合辅助，借助Set集合的特性（不存储相同元素），避免访问重复节点。
• 流程：将访问过的节点添加进集合，之后需要判断将要入队的节点是否存在于Set集合里。若有，则说明是已访问过的节点，不入队。反之，入队。

Queue<xxx> queue = new LinkedList<>();
Set<xxx> set = new LinkedList<>();
queue.add(..);//入队：尾部插入
while(!queue.isEmpty()){
	int size = queue.size();
	for (int i = 0; i < size; ++i){
		xx = queue.poll();//出队：头部取出
		set.add(xx);
		...
		if(... && set.contains(...)) queue.add(...);//添加其子节点入队
	}
	//若是解决最短路径等相关问题，需添加步长变量
	count++;
}

补充

举一个问题

• 当我们利用BFS在一个二维数组中寻找两点之间最短路径时，需要将当前节点位置的相邻位置全部入队，那么由于是二维数组就需要存储两个数值来确定一个坐标（x,y）。那么该怎样存储呢？

解决方案

1. 面向对象思想，将两个数值封装成一个坐标对象，最后将之入队。
2. 数学，在二维数组中，我们其实可以通过一个数字确定其位置：保证唯一性并反向推出下标。

Integer[][] num; int i = 2, h = 4; 
int m = num.length;//假设行数为4，因此m=4
int n = num[0].length;//假设列数为5，因此n=5
int x = i * n + j;//得到我们需要的数字了
此时x = 14
接下来反向推导
i == x / n;为 true
j == x % n;为 true