深度学习——激活函数（激励函数）理论学习

1. 什么是激活函数

f(z)函数会把输入信号的总和转换为输出信号，这种函数一般称为激活函数。如下图：

简化后：

2. 激活函数作用

如果不用激活函数，每一层输出都是上层输入的线性函数，无论神经网络有多少层，输出都是输入的线性组合，这种情况就是最原始的感知机。
如果使用的话，激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。
没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。

3. 常见的几种激活函数

3.1 Sigmoid激活函数

数学表达式如下：e约等于2.7182

函数图像如下：

优点：
把输入的连续实值变换为0和1之间的输出；平滑、容易求导。

缺点：

1. 在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。函数导数的图像如下：
   

如果我们初始化神经网络的权值为[0,1]之间的随机值，由反向传播算法的数学推导可知，梯度从后向前传播时，每传递一层梯度值都会减小为原来的0.25倍，如果神经网络隐层特别多，那么梯度在穿过多层后将变得非常小接近于0，即出现梯度消失现象；当网络权值初始化为( 1 , + ∞ )区间内的值，则会出现梯度爆炸情况。

2. 含有幂运算，随着网络层数增多，消耗的时间也会增加。

3.2 step function（阶跃函数）

函数图像如下：

数学表达式如下：

由图可以看出，阶跃函数的导数在绝大多数地方（除了0之外）的导数都是0。所以用它做激活函数的话，参数们的微小变化所引起的输出的变化就会直接被阶跃函数抹杀掉，在输出端完全体现不出来，训练时使用的损失函数的值就不会有任何变化，这是不利于训练过程的参数更新的。

3.3 Tanh(双曲正切函数)激活函数

数学表达式：

函数图像：

函数导数图像：

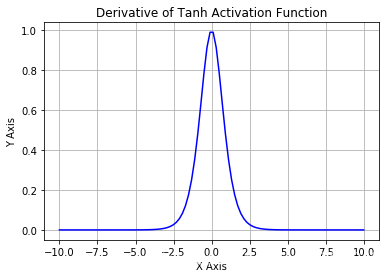
优点：

1. 解决了Sigmoid的输出不关于零点对称的问题；
2. 也具有Sigmoid的优点平滑，容易求导。

缺点：
梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

3.4 ReLU函数

函数图像如下：

数数表达式如下：

函数导数图像如下：

ReLU函数其实就是一个取最大值函数，注意这并不是全区间可导的。

优点：

1. 计算量小；
2. 收敛速度远快于sigmoid和tanh
3. 缓解了在深层网络中使用sigmoid和Tanh激活函数造成了梯度消失的现象（右侧导数恒为1）；
4. 缓解过拟合的问题。由于函数的会使小于零的值变成零，使得一部分神经元的输出为0，造成网络的稀疏性，减少参数相互依赖的关系缓解过拟合的问题。

缺点：

1. 造成神经元的**“死亡”**；
2. ReLU的输出不是0均值的。

对于ReLU神经元“死亡”解决方案：

1. 优化函数，使用Leaky ReLU函数；
2. 用较小的学习速率；
3. 采用momentum based优化算法，动态调整学习率。

3.5 Leaky ReLU函数（PReLU）

数学表达式：一般α=0.01

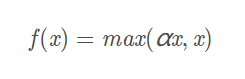
函数图像（左）函数导数图像（右）：

从函数图像来看，它和ReLU的区别在于负数那边的斜率不是0，而是0.01，非常接近0。一般α=0.01，也可由方向传播算法学出来。

3.6 ELU (Exponential Linear Units) 函数

数学表达式：

函数图像（左）及函数导数图像（右）：

ELU也是为解决ReLU存在的问题而提出，显然，ELU有ReLU的基本所有优点。

1. 不会有Dead ReLU问题
2. 输出的均值接近0，zero-centered

4. 如何选择合适的激活函数

1. 这个问题目前没有确定的方法，凭一些经验吧。
2. 深度学习往往需要大量时间来处理大量数据，模型的收敛速度是尤为重要的。所以，总体上来讲，训练深度学习网络尽量使用zero-centered数据 (可以经过数据预处理实现) 和zero-centered输出。所以要尽量选择输出具有zero-centered特点的激活函数以加快模型的收敛速度。
3. 如果使用ReLU，那么一定要小心设置learning rate，而且要注意不要让网络出现很多 “dead” 神经元，如果这个问题不好解决，那么可以试试Leaky ReLU、PReLU或者Maxout。
4. 最好不要用 sigmoid，你可以试试tanh，不过可以预期它的效果会比不上ReLU和Maxout.

参考资料：

https://blog.youkuaiyun.com/tyhj_sf/article/details/79932893
https://blog.youkuaiyun.com/neo_lcx/article/details/100122938
https://blog.youkuaiyun.com/colourful_sky/article/details/79164720
https://fuhailin.github.io/activation-functions/