对协方差矩阵 与 PCA(主成分分析) 的理解

协方差矩阵 与 主成分分析

一、协方差矩阵

我们知道，一个向量的方差的求法为：

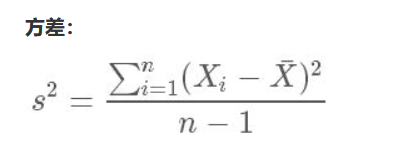
至于为什么分母为n-1，这里需要用到无偏估计的知识。

协方差矩阵就是描述两两维度间关系的矩阵：

两个维度的关系为：

那么一个三维矩阵数据集{x,y,z}的协方差矩阵就为：

因此，协方差矩阵是一个对称的矩阵，且对角线是各个维度的方差。

协方差矩阵还可以这样计算，先让样本矩阵中心化，即每一维度减去该维度的均值，使每一维度上的均值为0，然后直接用新的到的样本矩阵乘上它的转置，然后除以(N-1)即可。

二、主成分分析

主成分分析就是一个降维的过程。通过求得样本矩阵S的投影矩阵P1，然后通过投影矩阵求得协方差矩阵S1.

首先、我们需要求得样本矩阵的协方差矩阵C

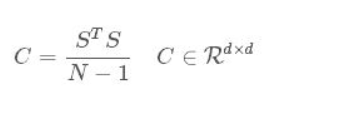
然后对该协方差矩阵进行对角化得到正交矩阵P和特征值矩阵Λ：

然后我们从Λ中取最大的前p个特征值构成新得对角阵Λ1，对应的p个特征向量构成了新的特征向量矩阵P1.

P1就为投影矩阵。假设PCA降维后的矩阵为S1，则根据PCA的目的，降噪与消灭冗余。各个维度间的协方差为0，也就是说S1的协方差矩阵为Λ1.

学习于：再谈协方差矩阵之主成分分析PCA