《深入掌握以太坊核心技术》--16-MPT

原创已于 2025-04-07 15:48:19 修改

· 1.4k 阅读

版权

文章标签：

于 2024-05-30 20:17:43 首次发布

14 篇文章

订阅专栏

某数树的问题
数据校验

基数树节点之间的连接方式是指针，一般是用32位或64位的内存地址作为指针的值，比如C语言就是这么做的。但这种直接存地址的方式无法提供对数据内容的校验，而这在区块链这样的分布式系统中非常重要。

访问效率

基数树的另一个问题是低效。如果我们只想存一个bytes32
类型的键值对，访问路径长度就是64(在以太坊定义的Hex字符集下);每一级访问的节点都至少需要存储16个字节，这样就需要至少1k
字节的额外空间，而且每次查找和删除都必须完整地执行 64 次下探访问。

梅克尔-帕特里夏树是梅克尔树和帕特里夏树的结合
以太坊中的实现，对key采用Hex编码，每个Hex字符就是一个nibble(半字节)
遍历路径时对一个节点只访问它的一个nibble，大多数节点是一个包含17个元素的数组;其中16个分别以hex字符作为索引值，存储路径中下一个nibble的指针;另一个存储如果路径到此已遍历结束，需要返回的最终值。这样的节点叫做“分支节点”(branch node)
分支节点的每个元素存储的是指向下一级节点的指针。与传统做法不同，MPT是用所指向节点的hash来代表这个指针的;每个节点将下个节点的hash作为自己存储内容的一部分，这样就实现了Merkel树结构，保证了数据校验的有效性

MPT 中的节点有以下几类

对于64个字符的路径长度，很有可能在某个节点处会发现，下面至少有一段路径没有分叉;这很难避免
我们当然可以依然用标准的分支节点来表示，强制要求这个节点必须有完整的16个索引，并给没有用到的那15个位置全部赋空值;但这样有点蠢
通过设置“扩展节点”，就可以有效地缩短访问路径，将几长的层级关系压缩成一个键值对，避免不必要的空间浪费
扩展节点(extensionnode)的内容形式是[encodedPath,key],其中
encodedPath包含了下面不分叉的那部分路径，key是指向下一个节点的指针(hash，也即在底层db中的存储位置)
叶子节点(leafnode):如果在某节点后就没有了分又路径，那这是一个叶子节点，它的第二个元素就是自己的value

路径压缩的处理相当于实现了压缩前缀树的功能;不过路径表示是Hex字符串(nibbles)，而存储却是以字节(byte)为单位的，这相当于浪费了一倍的存储空间
我们可以采用一种紧凑编码(compactcoding)方式，将两个nibble整合在一个字节中保存，这就避免了不必要的浪费
这里就会带来一个问题:有可能nibble总数是一个奇数，而数据总是以字节形式存储的，所以无法区分nibble1和nibbles01;这就使我们必须分别处理奇偶两种情况
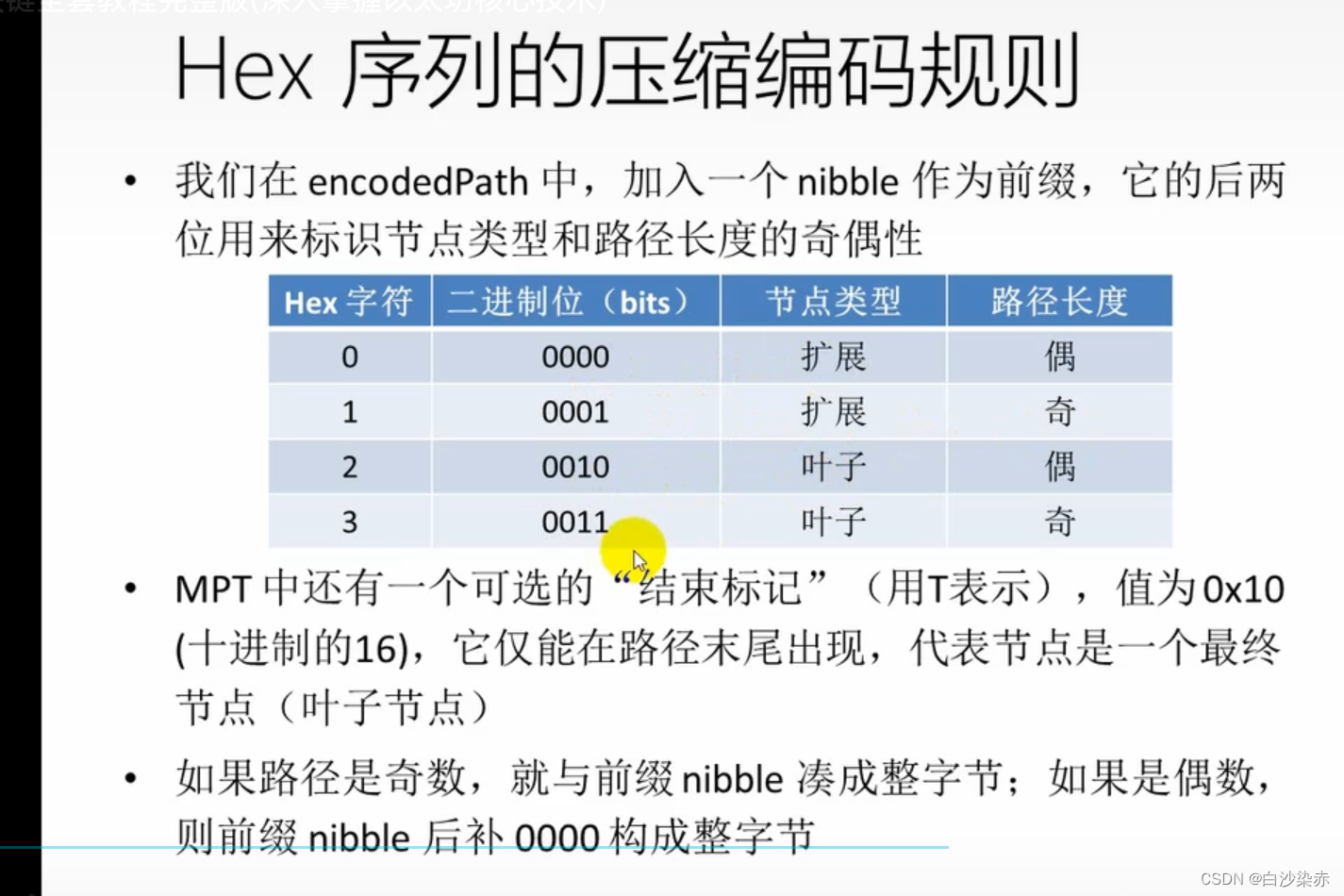
为了区分路径长度的奇偶性，我们在encodedPath中引入标识位

在这里插入图片描述

以太坊中所有的merkel树都是MPT
在一个区块的头部(blockhead)中，有三颗MPT的树根:
- stateRoot
  - 状态树的树根
- transactionRoot
  - 交易树的树根
- receiptsRoot
  - 收据树的树根
状态树(state trie)
- 世界状态树，随时更新;它存储的键值对(path,value)可以表示为(sha3(ethereumAddress),rlp(ethereumAccount))
- 这里的 account是4个元素构成的数组:[nonce,balance,storageRoot,codeHash]
存储树(storage trie)
- 存储树是保存所有合约数据的地方;每个合约账户都有一个独立隔离的存储空间
交易树(transaction trie)
- 每个区块都会有单独的交易树;它的路径(path)是rlp(transactionIndex)，只有在挖矿时才能确定;一旦出块，不再更改
收据树(receipts trie)
- 每个区块也有自己的收据树;路径也表示为rp(transactionIndex)