机器学习——回归分析和线性回归

一、机器学习

1.1机器学习的概念

• 从数据中寻找规律、建立关系，根据建立的关系去解决问题

1.2机器学习的学习框架

• 训练数据x,y 自动求解x,y的关系 新数据预测

1.3机器学习的四大学习方法类别

1.31监督学习

• 有正确的标签
• 价格预测，图像识别，语言翻译
• 线性回归，逻辑回归，决策树，朴素贝叶斯，KNN

1.32无监督学习

• 没有正确的标签
• 客户划分，新闻聚类，数据降维
• 聚类算法，PCA降维，异常检测

1.33半监督学习

• 有少量正确标签
• 混合学习应用

1.34强化学习

• 建立奖惩机制
• OpenAi Five ,AiphaGo

1.35场景

• 任务复杂、采集大量数据有难度
• 解决办法：大部分场景都需要监督学习，条件允许的情况下尽可能收集足够的样本，无法收集足够样本的条件下，考虑标签样本+无标签样本实现监督学习与无监督学习的结合，即半监督学习
• 大部分应用场景中，条件允许的情况下，优先考虑监督学习；
• 部分特定的场景，无监督学习能够帮我们找到“惊喜”（预料之外的数据关系）
• 未来的一大方向：监督+无监督，实现少量标签样本下的数据学习，在保证精度的同时极大降低数据采集难度

二、线性回归

2.1损失函数

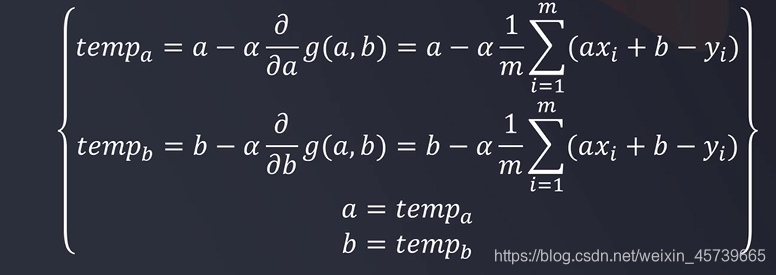
2.2梯度下降法

• 寻找函数极小值的一种方法
• 计算开始点Xi对应梯度，以一定步长向梯度反方向到达新的点Xi+1,重复此过程，直到Xi,Xi+1几乎不再发生变化
• 
  

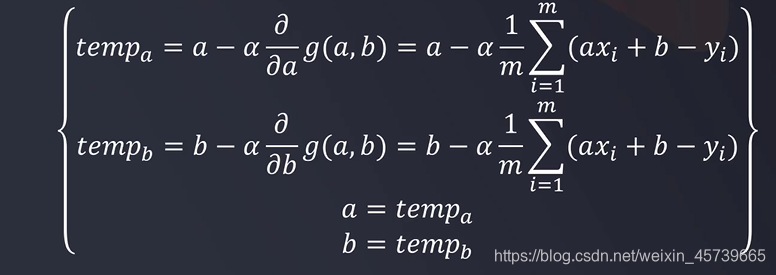
2.3线性回归流程

三.Scikit-learn

3.1Scikit-learn介绍

• 针对机器学习应用而开发的算法库
• 数据预处理、分类、回归、降维、模型选择等常用的机器学习算法
• 丰富的算法模块、易于安装与使用、样例丰富、教程文档详细
• //https://scikit-learn.org/stable/index.html

四.任务

4.1基于数据，建立单因子线性回模型，预测面积100平方米的房子售价100万是否值得投资

import pandas as pd
import numpy as np

data=pd.read_csv("data_hp.csv")
data.head()

# 数据预处理
from matplotlib import pyplot as plt
fig1=plt.figure()

# x，y赋值
x=data.loc[:,'面积']
y=data.loc[:,'房价']

#数据格式化
x=np.array(x)
x=np.array(x).reshape((len(x),1))
y=np.array(y)
y=np.array(y).reshape((len(y),1))

plt.scatter(x,y)
plt.xlabel("size(x)")
plt.ylabel("price(y)")
plt.show()

#模型建立及训练
from sklearn.linear_model import LinearRegression
model=LinearRegression()

#模型训练
model.fit(x,y)

#获取线性回归模型系数
a=model.coef_
b=model.intercept_
print(a,b,"y=f(x)={}*x+{}".format(a[0][0],b[0]))

#结果预测
x=100
y_predict=a[0][0]*x+b[0]
print(y_predict)

#第二种预测方法
X_test=np.array([[100]])
y_predict2=model.predict(X_test)
print(y_predict2)

#模型评估
from sklearn.metrics import mean_sqared_error,r2_score
MSE=mean_sqared_error(y,y_predict)
R2=r2_score(y,y_predict)
print(MSE,R2)
#MSE越小越好，R2越接近1越好

#预测结果可视化
from matplotlib import pyplot as plt
fig1=plt.figure()
plt.scatter(x,y,label="y_real")
plt.plot(x,y_predict,label="y_predict")
plt.xlabel("size(x)")
plt.ylabel("price(y)")
plt.legend()
plt.show()

4.2基于数据，建立多因子线性回模型，与只使用因子X1进行建模预测的结果进行对比

• 以面积为输入变量，建立单因子模型，评估模型表现，可视化线性回归预测结果
• 以面积、人均收入、平均房龄为输入变量，建立多因子模型，评估模型表现
• 预测面积=160，人均收入=70000，平均房龄=5的合理房价
• 

# In[]
import numpy as np
import pandas as pd

data2=pd.read_csv("data2_hp.csv")



# In[]
from matplotlib import pyplot as plt
fig=plt.figure(figsize=(20,5))
fig1=plt.subplot(131)
plt.scatter(data2.loc[:,'面积'],data2.loc[:,'价格'])
plt.title('Price VS Size')
plt.show()


fig2=plt.subplot(131)
plt.scatter(data2.loc[:,'人均收入'],data2.loc[:,'价格'])
plt.title('Price VS Income')
plt.show()

fig3=plt.subplot(131)
plt.scatter(data2.loc[:,'平均房龄'],data2.loc[:,'价格'])
plt.title('Price VS House_age')
plt.show()
# In[]
x=data2.loc[:,'面积']
y=data2.loc[:,'价格']

x=np.array(x).reshape(-1,1)
y=np.array(y).reshape(-1,1)

# In[]
plt.scatter(x,y)
plt.xlabel("size(x)")
plt.ylabel("price(y)")
plt.show()

# In[]
from sklearn.linear_model import LinearRegression
model=LinearRegression()

model.fit(x,y)

# In[]
y_predict=model.predict(x)
print(y_predict)

# In[]
from sklearn.metrics import mean_squared_error,r2_score
MSE=mean_squared_error(y,y_predict)
R2=r2_score(y, y_predict)
print(MSE)
print(R2)


# In[]
from matplotlib import pyplot as plt
fig2=plt.figure(figsize=(8,5))
plt.scatter(x,y,label="y_real")
plt.plot(x,y_predict,'r',label="y_predict")
plt.xlabel("size(x)")
plt.ylabel("price(y)")
plt.legend()
plt.show()


# In[]
# x y再次赋值
x= data2.drop(['价格'],axis=1)
y=data2.loc[:,'价格']

# In[]
#建立多因子回归模型，并且训练
model_multi=LinearRegression()
model_multi.fit(x,y)

# In[]
#多因子模型的预测
y_predict_multi=model_multi.predict(x)
print(y_predict_multi)




# In[]
from sklearn.metrics import mean_squared_error,r2_score
MSE=mean_squared_error(y,y_predict_multi)
R2=r2_score(y, y_predict_multi)
print(MSE)
print(R2)

# In[]
#可视化预测结果
fig3=plt.Figure(figsize=(8,5))
plt.scatter(y, y_predict_multi)
plt.xlabel('real price')
plt.ylabel('predict')

plt.show()




# In[]
X_test=np.array([[160,70000,5]])
y_test_predict=model_multi.predict(X_test)
print(y_test_predict)