排序算法

选择排序

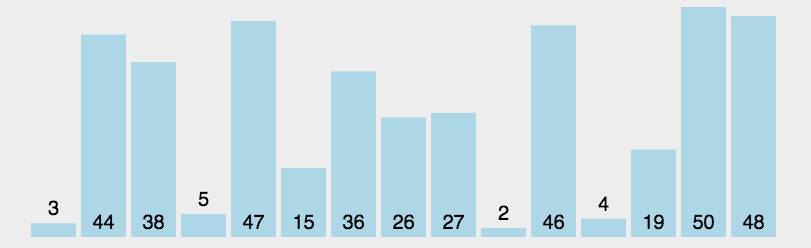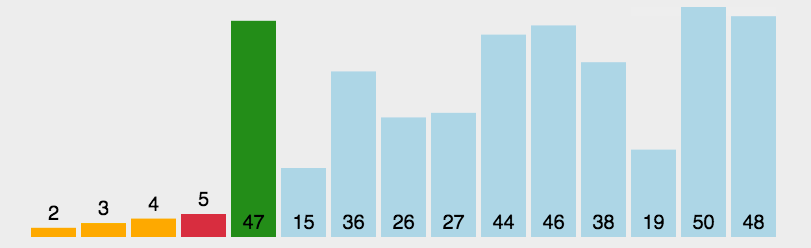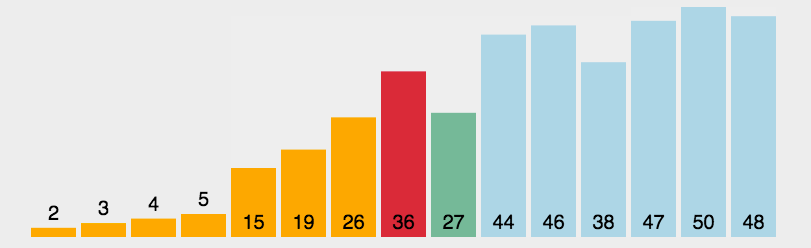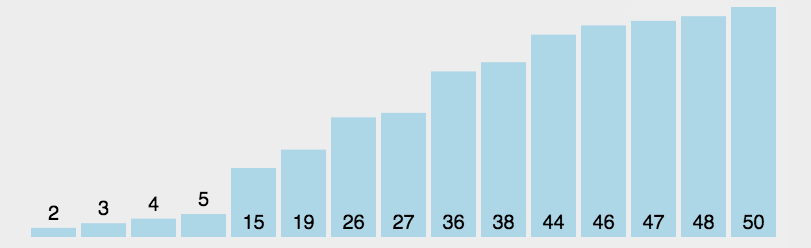
从数组中选择最小元素，将它与数组的第一个元素交换位置。再从数组剩下的元素中选择出最小的元素，将它与数组的第二个元素交换位置。不断进行这样的操作，直到将整个数组排序。

    public static void selectSort(int[] arr) {
        for (int i = 0; i < arr.length - 1; i++) {
            int k = 0;
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[j] < arr[k]) {
                    k = j;
                }
            }
            if (k != i) {
                int temp = arr[i];
                arr[i] = arr[k];
                arr[k] = temp;
            }
        }
    }

冒泡排序

从左到右不断交换相邻逆序的元素，在一轮的循环之后，可以让未排序的最大元素上浮到右侧。在一轮循环中，如果没有发生交换，那么说明数组已经是有序的，此时可以直接退出

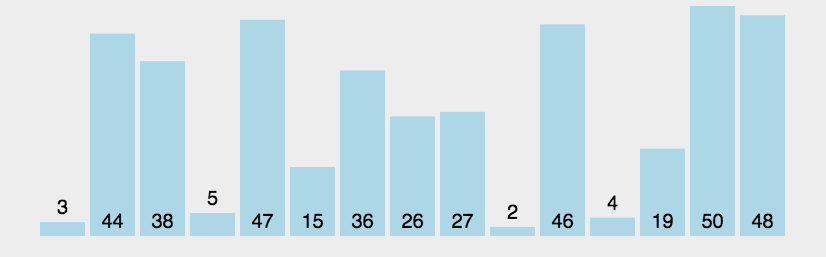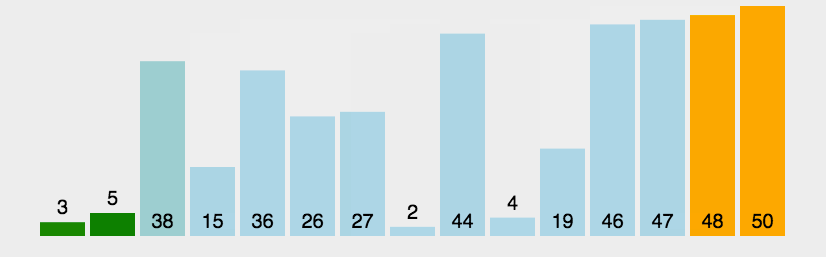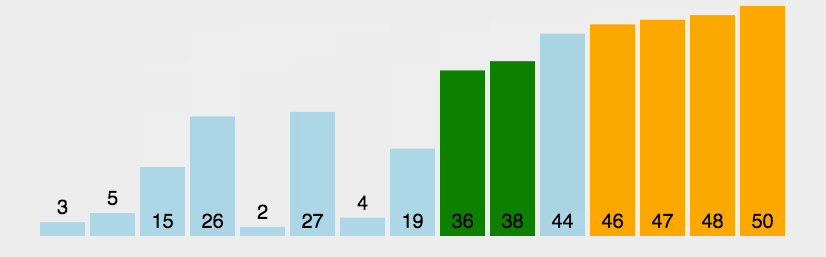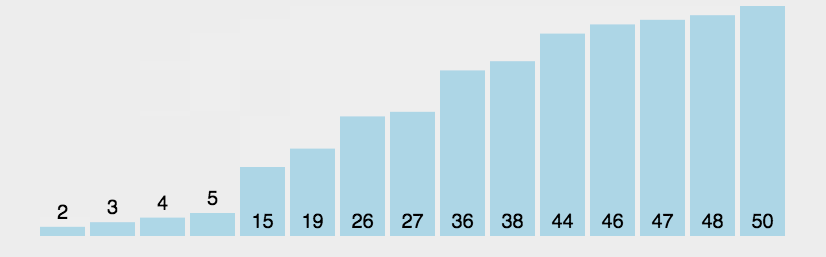
    public static void bubbleSort(int[] arr) { // 设置每次冒泡的终止点
        for (int i = arr.length - 1; i > 0; i--) {
            boolean change = false; // 从起点开始冒泡
            for (int j = 0; j < i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    if (change == false) {
                        change = true;
                    }
                }
            }

        }
    }

插入排序

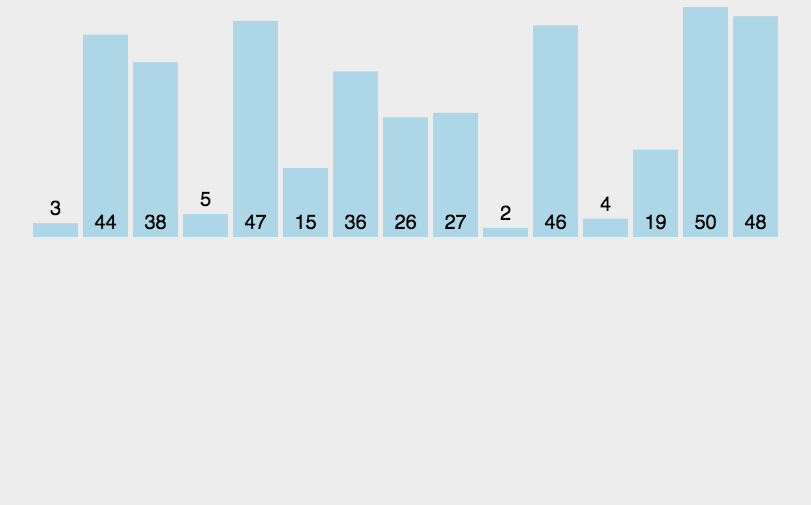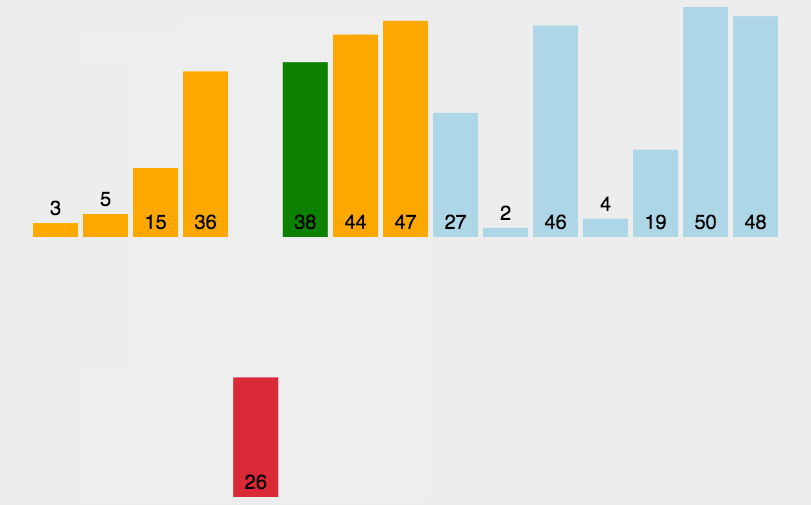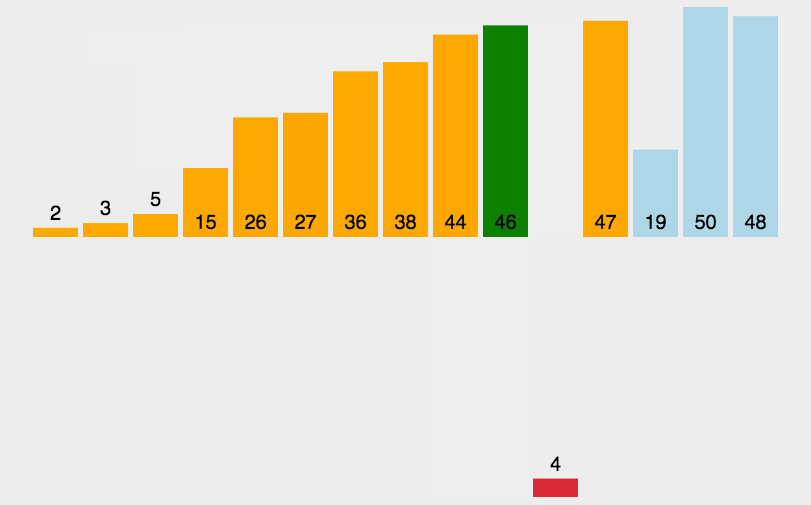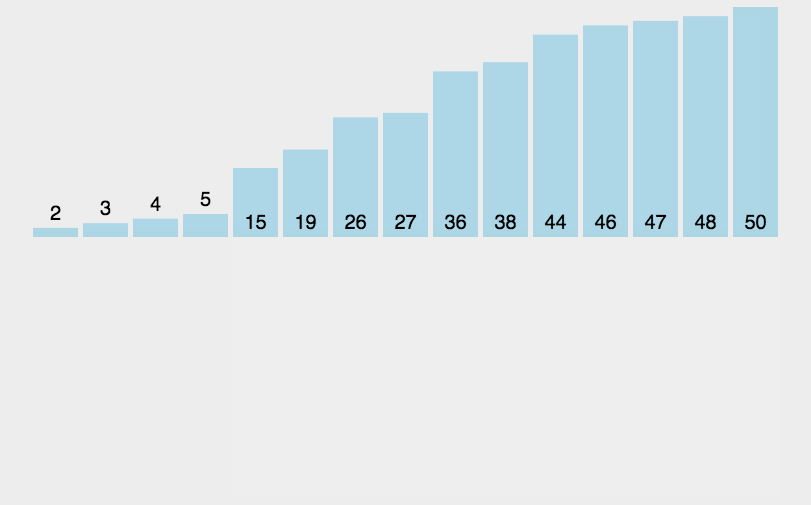
通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。每步将一个待排序的元素，按其排序码大小插入到前面已经排好序的一组元素的适当位置上去，直到元素全部插入为止。

    public static void insertionSort(int[] arr) {
        // 从第二个元素开始为它们找位置 
        for (int i = 1; i < arr.length; i++) {
            // 记住当前元素 
            int temp = arr[i];
            int j;
            // 从当前元素左边第一个元素开始，向左找位置 
            for (j = i - 1; j >= 0 && arr[j] > temp; j--) {
                arr[j + 1] = arr[j];
            }
            // 找到合适位置后，将当前元素插入 
            arr[j + 1] = temp;
        }
    }

希尔排序

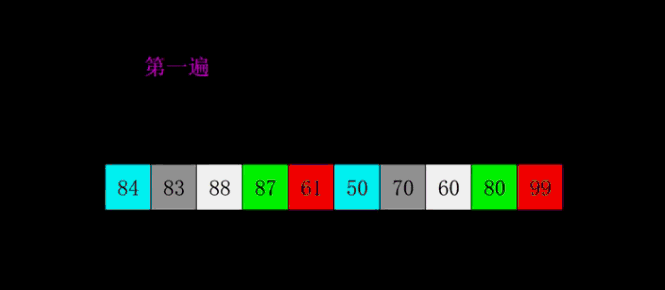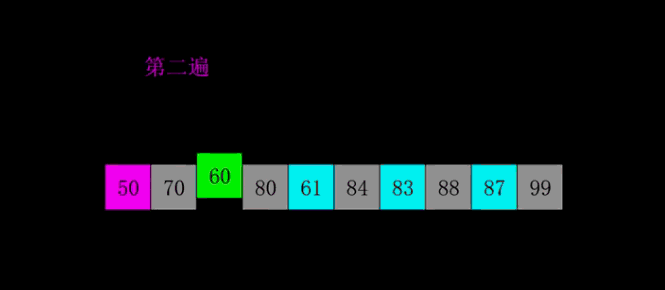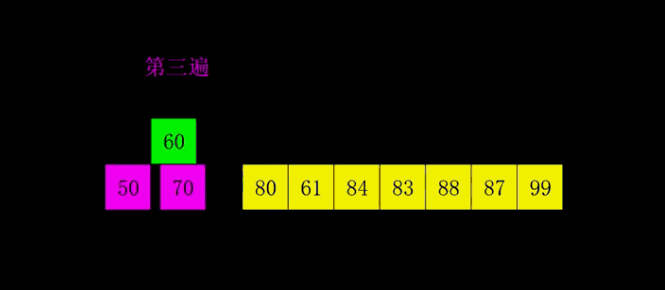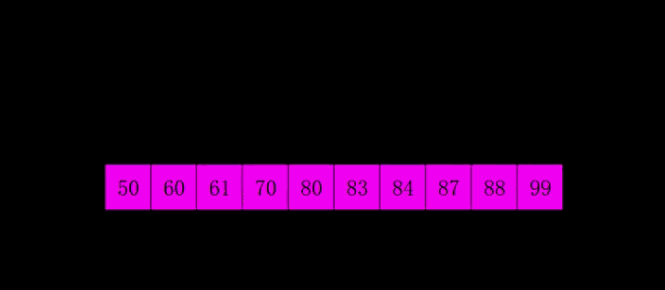
又称“分组插入排序”，先将整个待排元素序列分割成若干个子序列（由相隔某个“增量”的元素组成的）分别进行直接插入排序，然后依次缩减增量再进行排序，待整个序列中的元素基本有序（增量足够小）时，再对全体元素进行一次直接插入排序。

    public static void shellSort(int[] arr) {
        // 增量控制，每次减半
        for (int gap = arr.length / 2; gap > 0; gap /= 2) {
            // 步长控制，从gap开始向后移动
            for (int i = gap; i < arr.length; i++) {
                int temp = arr[i];
                int j;
                // 起始指针控制，向左插入排序（找位置）
                for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap) {
                    arr[j + gap] = arr[j];
                }
                arr[j + gap] = temp;
            }
        }
    }

归并排序

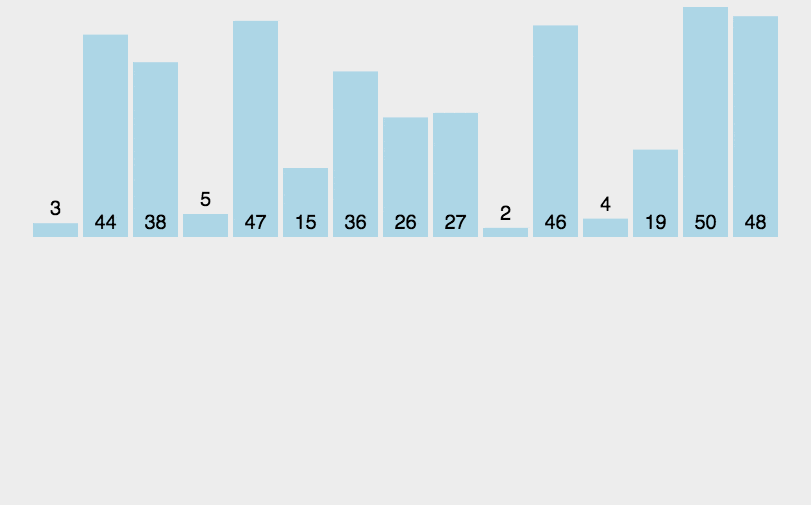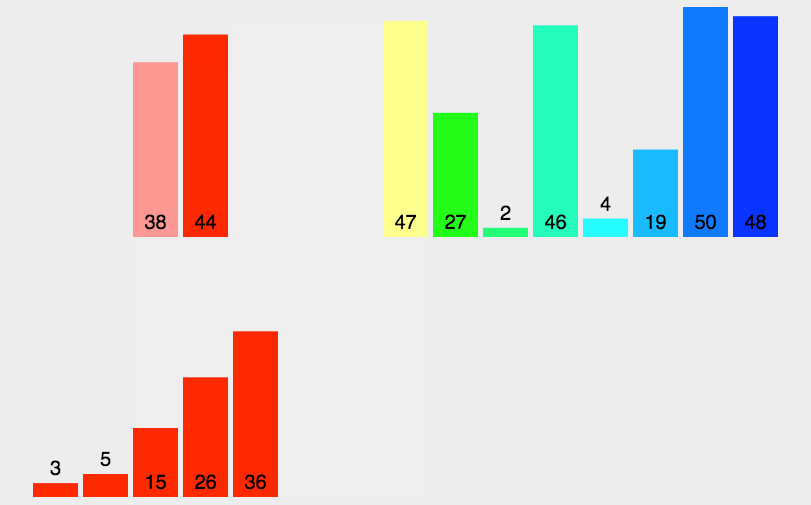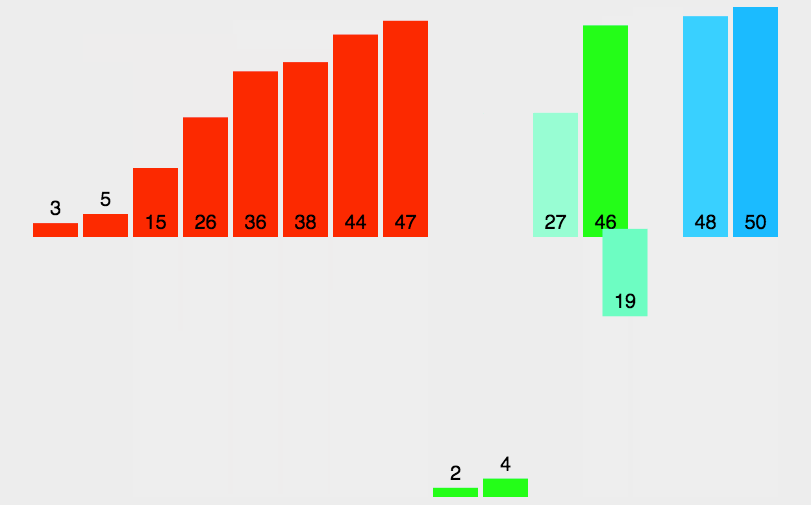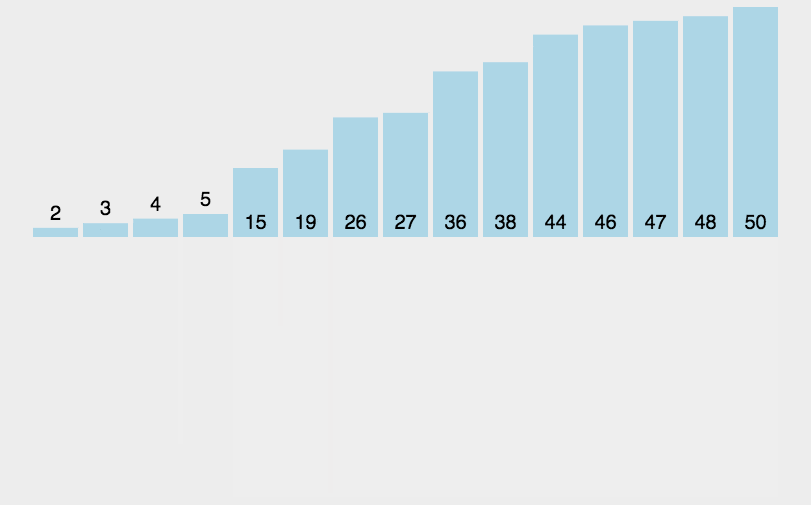
该算法采用经典的分治（divide-and-conquer）策略，分：问题分成一些小的问题然后递归求解，治：将分的阶段得到的各答案"修补"在一起，即分而治之。将序列递归拆分成多个子序列，再将各个子序列排序后归并叠加，最后归并所有子序列，排序完成。

    public static void mergeSort(int[] arr, int left, int right) {
        if (left < right) {
            int mid = (left + right) / 2;
            // 分 
            mergeSort(arr, left, mid);
            mergeSort(arr, mid + 1, right);
            // 治 
            merge(arr, left, mid, right);
        }
    }

    public static void merge(int[] arr, int left, int mid, int right) {
        // 临时数组 
        int[] temp = new int[right - left + 1];
        // 左、右指针 
        int i = left;
        int j = mid + 1;
        int k = 0;
        // 将两段数据按序写入临时数组 
        while (i <= mid && j <= right) {
            if (arr[i] <= arr[j]) {
                temp[k++] = arr[i++];
            } else {
                temp[k++] = arr[j++];
            }
        }
        // 剩余数据写入
        while (i <= mid) {
            temp[k++] = arr[i++];
        }
        while (j <= right) {
            temp[k++] = arr[j++];
        }
        // 更新arr数组 
        k = 0;
        while (left <= right) {
            arr[left++] = temp[k++];
        }
    }

快速排序

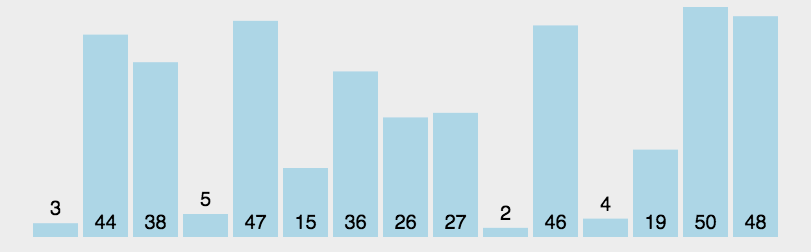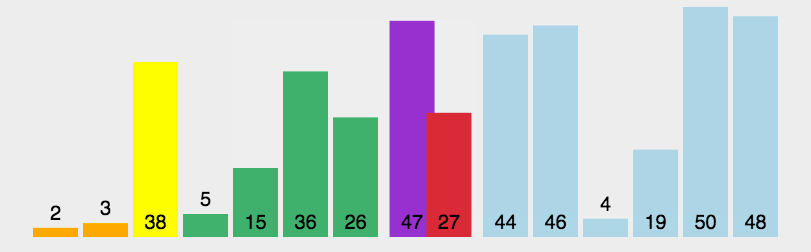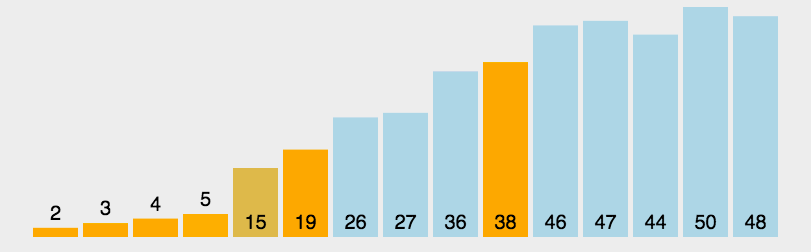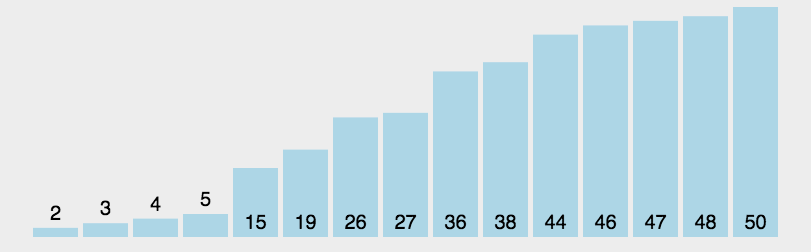
以第一个元素为基准，左右指针向中间移动扫描，小于基准元素的放到左边，大于基准元素的放到右边，最后将基准元素放到中间，这个位置也就是基准元素的合适位置。此时数据以基准元素为间隔，分为左右两部分（不包括基准元素），然后分别对左右两部分数据分别执行此过程，直到数据不能再分，此时排序完成。

 public static void quickSort(int[] arr, int left, int right) {
        if (left < right) {
            int index = getIndex(arr, left, right);
            quickSort(arr, left, index - 1);
            quickSort(arr, index + 1, right);
        }
    }

    public static int getIndex(int[] arr, int left, int right) {
        // 得到基准元素
        int item = arr[left];
        // 向中间移动，调整位置，找到基准元素的位置
        while (left < right) {
            while (left < right && arr[right] >= item) {
                right--;
            }
            arr[left] = arr[right];
            while (left < right && arr[left] <= item) {
                left++;
            }
            arr[right] = arr[left];
        }
        // 放置基准元素
        arr[left] = item;
        return left;
    }

堆排序

将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

    public static void heapSort(int[] arr) {
        // 1.构建大顶堆
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            adjust(arr, i, arr.length);
        }
        // 2.调整堆结构，交换顶元素与末尾元素
        for (int j = arr.length - 1; j > 0; j--) {
            int temp = arr[j];
            arr[j] = arr[0];
            arr[0] = temp;
            adjust(arr, 0, j);
        }
    }

    public static void adjust(int[] arr, int i, int length) {
        int temp = arr[i];
        for (int k = 2 * i + 1; k < length; k = 2 * k + 1) {
            if (k + 1 < length && arr[k + 1] > arr[k]) {
                k++;
            }
            if (arr[k] > temp) {
                arr[i] = arr[k];
                i = k;
            } else {
                break;
            }
        }
        arr[i] = temp;
    }

计数排序

计数排序要求输入的数据必须是有确定范围的整数。

找出待排序的数组中最大和最小的元素；统计数组中每个值为i的元素出现的次数，存入数组C的第i项；对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）；反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

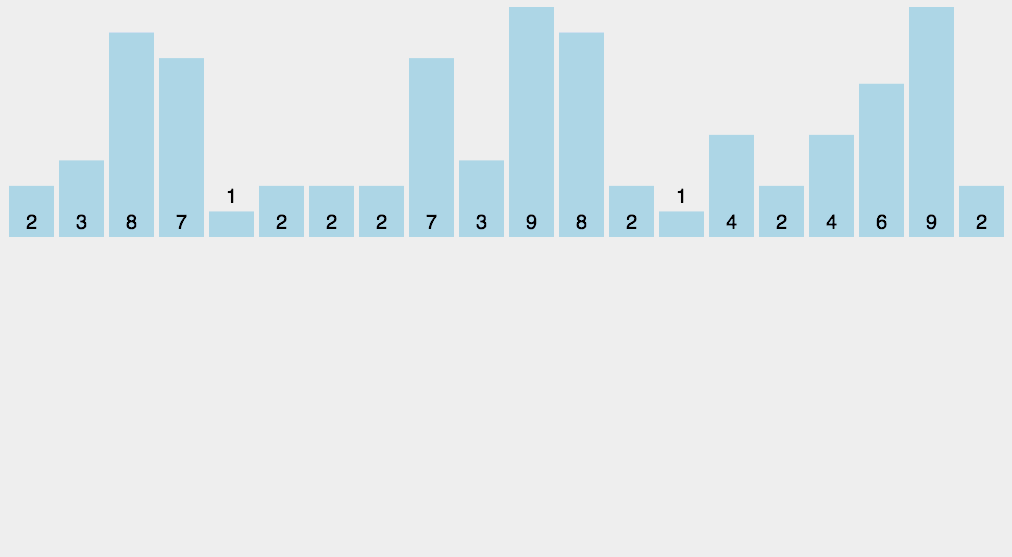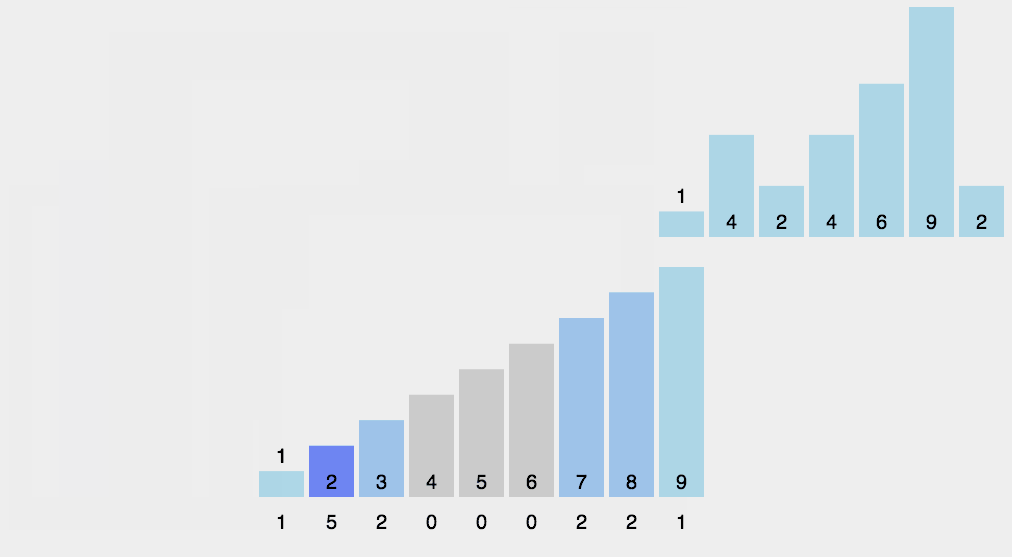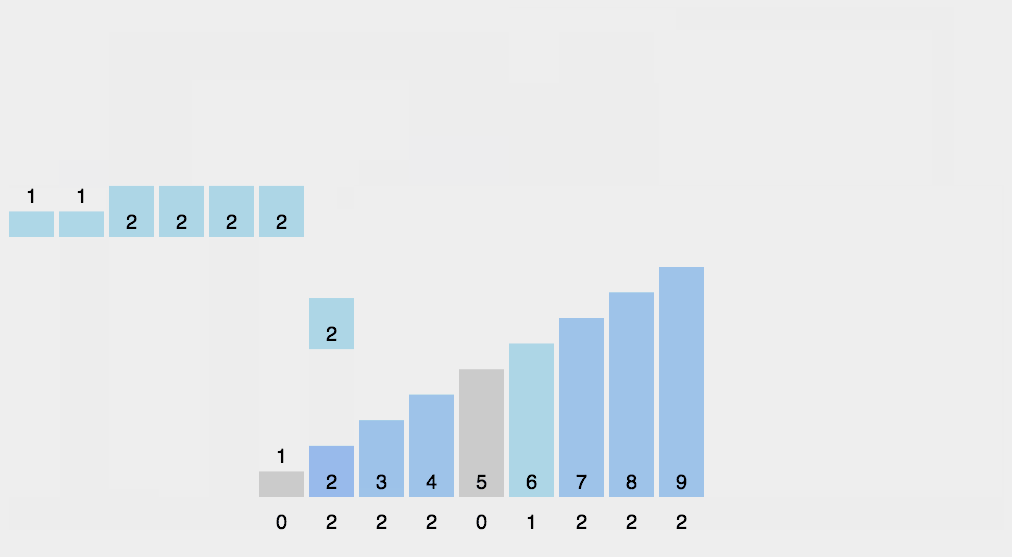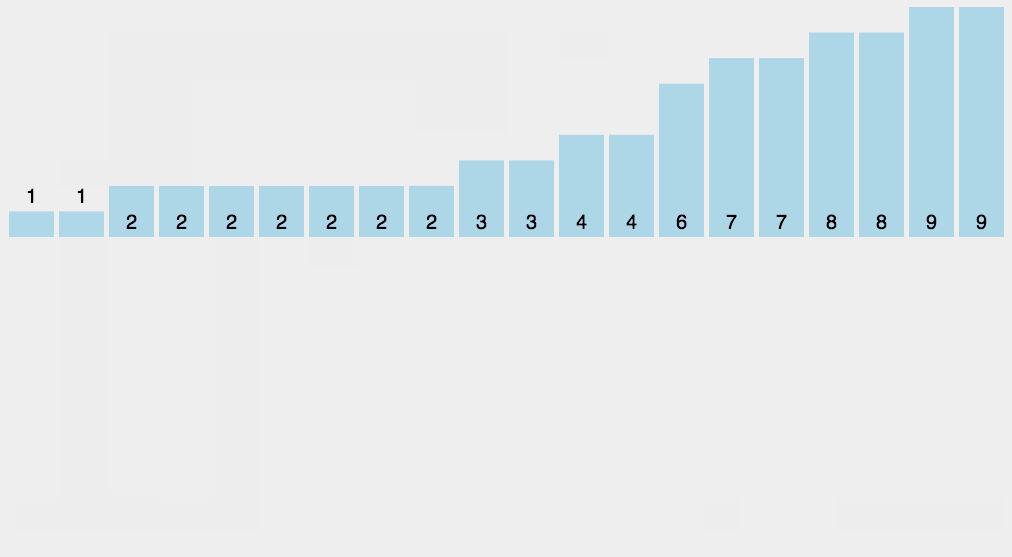
    public static int[] countSort(int[] src) {
        // 计算最大值与最小值 
        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < src.length; i++) {
            max = Math.max(max, src[i]);
            min = Math.min(min, src[i]);
        }
        // 数组中的数据范围 
        int range = max - min + 1;
        // count[i]表示数组src中数据min + I的个数 
        int[] count = new int[range];
        for (int value : src) {
            count[value - min]++;
        }
        // 累计变形，使得count[i]保存src中小于等于min + i的数据的个数
        for (int i = 1; i < range; i++) {
            count[i] += count[i - 1];
        }
        // 结果数组 
        int[] res = new int[src.length];
        // 倒序遍历原数组，保持排序的稳定性
        for (int i = src.length - 1; i >= 0; i--) {
            // 获取数据在count数组中的索引
            int index = src[i] - min;
            // 个数减1 
            count[index]--;
            // 数据src[i]排序后的索引是count[index] 
            res[count[index]] = src[i];
        }
        return res;
    }

桶排序

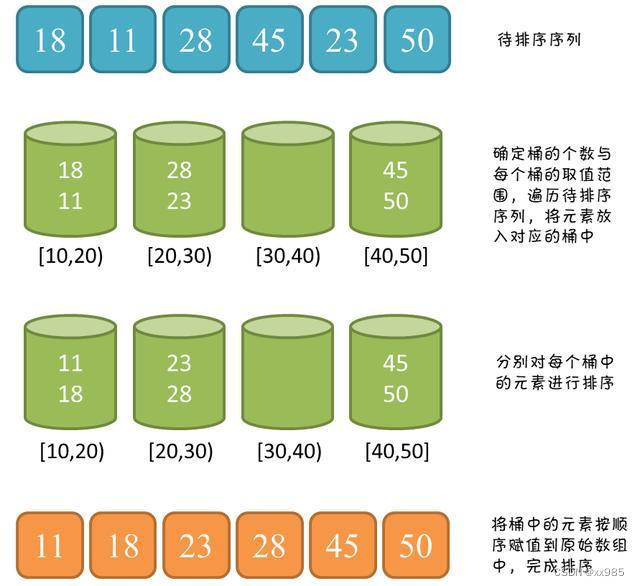
桶排序是计数排序的扩展版本，计数排序可以看成每个桶只存储相同元素，而桶排序每个桶存储一定范围的元素，通过映射函数，将待排序数组中的元素映射到各个对应的桶中，对每个桶中的元素进行排序，最后将非空桶中的元素逐个放入原序列中。

桶排序需要尽量保证元素分散均匀，否则当所有数据集中在同一个桶中时，桶排序失效。

    public static void bucketSort(int[] arr) {
        // 计算最大值与最小值
        int max = Integer.MIN_VALUE;
        int min = Integer.MAX_VALUE;
        for (int i = 0; i < arr.length; i++) {
            max = Math.max(max, arr[i]);
            min = Math.min(min, arr[i]);
        }
        // 计算桶的数量,并创建桶 
        int bucketNum = (max - min) / arr.length + 1;
        ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
        for (int i = 0; i < bucketNum; i++) {
            bucketArr.add(new ArrayList<Integer>());
        }
        // 将每个元素放入桶
        for (int i = 0; i < arr.length; i++) {
            int num = (arr[i] - min) / (arr.length);
            bucketArr.get(num).add(arr[i]);
        }
        // 对每个桶进行排序 
        for (int i = 0; i < bucketArr.size(); i++) {
            Collections.sort(bucketArr.get(i));
        }
        // 将桶中的元素赋值到原序列 
        int index = 0;
        for (int i = 0; i < bucketArr.size(); i++) {
            for (int j = 0; j < bucketArr.get(i).size(); j++) {
                arr[index++] = bucketArr.get(i).get(j);
            }
        }
    }

基数排序

基数排序可以看成是桶排序的扩展，以整数排序为例，主要思想是将整数按位数划分，准备 10 个桶，代表 0 - 9，根据整数个位数字的数值将元素放入对应的桶中，之后按照输入赋值到原序列中，依次对十位、百位等进行同样的操作，最终就完成了排序的操作。

    public static void radixSort(int[] arr) {
        if (arr == null || arr.length < 2) {
            return;
        }
        radixSort(arr, 0, arr.length - 1, maxbits(arr));
    }

    // 计算最大位数
    public static int maxbits(int[] arr) {
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < arr.length; i++) {
            max = Math.max(max, arr[i]);
        }
        int res = 0;
        while (max != 0) {
            res++;
            max /= 10;
        }
        return res;
    }

    // 基数排序
    public static void radixSort(int[] arr, int begin, int end, int digit) {
        final int radix = 10;
        int i = 0, j = 0;
        int[] count = new int[radix];
        int[] bucket = new int[end - begin + 1];
        // 依次遍历每个位数
        for (int d = 1; d <= digit; d++) {
            for (i = 0; i < radix; i++) {
                count[i] = 0;
            }
            // 统计数量
            for (i = begin; i <= end; i++) {
                j = getDigit(arr[i], d);
                count[j]++;
            }
            // 计算位置
            for (i = 1; i < radix; i++) {
                count[i] = count[i] + count[i - 1];
            }
            // 记录到对应位置
            for (i = end; i >= begin; i--) {
                j = getDigit(arr[i], d);
                count[j]--;
                bucket[count[j]] = arr[I];
            }
            for (i = begin, j = 0; i <= end; i++, j++) {
                arr[i] = bucket[j];
            }
        }
    }

    // 获取位数数值
    public static int getDigit(int x, int d) {
        return ((x / ((int) Math.pow(10, d - 1))) % 10);
    }

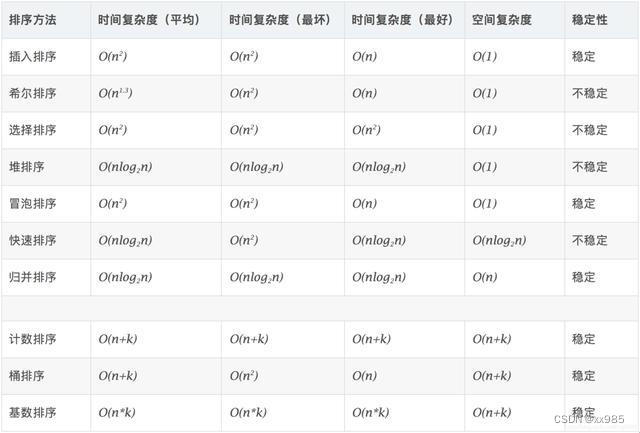
算法分类及适用场景

★ 选择、冒泡、插入、希尔、归并、快速、堆排序都是基于比较的排序。

平均时间复杂度最低O(nlogn)。

适用于所有可比较的对象。

★ 计数排序、桶排序、基数排序不是基于比较的排序。

使用空间换时间，某些时候，平均时间复杂度可以低于O(nlogn)。

适用于正整数的比较。

稳定性分析

不稳定的排序算法有：快速排序、希尔排序、选择排序、堆排序。

巧记：快『快速排序』、些『希尔排序』、选『选择排序』、堆『堆排序』。

稳定的排序算法有：冒泡排序、插入排序、归并排序、计数排序、桶排序、基数排序。

原文