Lumerical官方案例、FDTD时域有限差分法仿真学习（十）——光栅耦合器（Grating coupler）

设计一个光栅耦合器，将光子芯片表面的单模光纤连接到集成波导。 内置粒子群优化工具用于最大化耦合效率，并使用组件 S 参数创建 INTERCONNECT 中的紧凑模型。 它还展示了如何使用 CML 编译器提取这些参数以生成紧凑模型。

一、概述

了解模拟工作流程和关键结果

本示例的目标是设计一个 TE 绝缘体上硅 (SOI) 耦合器，该耦合器带有一个布拉格光栅，由单模光纤从顶部输入。 此设计中的关键品质因数 (FOM) 是目标波长处的耦合效率。 耦合效率对光栅的周期 $p$、蚀刻长度 $l_e$ 和蚀刻深度$h_e$以及光纤的位置 x 和倾斜角 θ 高度敏感。

这五个参数通常一起优化，以最大化目标中心波长处的耦合效率。 由于具有五个参数的强力 3-D 优化非常耗时，因此此处使用 2-D 和 3-D 模型的组合并仅改变三个几何参数进行两阶段优化。 设计工作流程包括四个主要步骤。

1.初始二维优化：优化光栅周期 p、占空比 d 和光纤位置 x。
2.最终的 3-D 优化：优化光纤的位置 x 以最小化插入损耗。
3.S 参数提取：运行 S 参数扫描并将结果导出到数据文件。
4.紧凑模型创建：将 S 参数数据导入光学 S 参数元素。

如下一节所示，主要使用二维模拟并改变光栅的周期、占空比和光纤的位置，可以获得高于 40% 的峰值耦合效率。

使用 CML 编译器生成紧凑模型

要使用 CML Compiler 生成光栅耦合器的紧凑模型，可以使用步骤 3 中的 S 参数数据。 CML 编译器的参数提取（Parameter extraction for CML Compiler）章节部分展示了如何使用脚本文件自动运行步骤 3 并生成 S 参数数据。 已经熟悉此示例的高级用户可以直接进入本节。 如果您不熟悉此示例，我们强烈建议您先阅读前面的部分并了解各个步骤，然后再转到 CML 编译器的参数提取部分。

二、运行和结果

运行模型的说明和关键结果的讨论

2.1 第 1 步：2D 优化

1.打开二维模拟文件。
2.通过转到“优化和扫描”（Optimizations and Sweeps）窗口并打开名为“耦合效率优化”（coupling efficiency optimization）的优化项来查看优化设置。
3.查看设置后，关闭编辑窗口并运行优化。 优化应在十到二十分钟内完成。 如果您不想等待，请直接进入最后的 3D 优化步骤。
4.优化完成后，即可检索最佳周期、占空比和位置。 左键单击“耦合效率优化”（coupling efficiency optimization）项，然后在上下文菜单中选择“可视化”（coupling efficiency optimization），然后选择“最佳参数”（best parameters）。

优化完成后，最佳参数结果也将显示在优化状态（optimization status）窗口中，如下所示。 品质因数图还显示，FOM 作为优化的结果已经最大化。

2.1.1 仿真结构

这里用的是SiO2包层（cladding)，优先级设置为较低的3，是为了能让后面的光栅结构嵌进去（优先级为2).

光栅结构类似于学习笔记（二）宽带光栅耦合器中的设置

index：waveguide部分折射率
targtet lengtth：光栅部分目标长度，实际长度将限制为整数个周期
h total：光栅总厚度
etch depth：刻蚀深度
duty cycle：占空比
ptich：光栅周期
input length：输入波导长度
output length：输出波导长度

fiber结构：

core diameter：芯层直径
cladding diameter：包层直径
y span：长度
theta：倾斜角度
core index：芯层折射率
cladding index：包层折射率

Script学习

# materials
core_index = %core index%; # 芯层折射率
cladding_index = %cladding index%; # 包层折射率

# update core material
setnamed("core","index",core_index);

# update cladding material
setnamed("cladding","index",cladding_index);

# dimensions
core_radius = %core diameter%/2.0; # 求对应的半径
cladding_radius = %cladding diameter%/2.0;

# update core dimensions
theta_rad = theta/(180/pi); # 将角度转化为弧度制
L = %y span%/cos(theta_rad); # 光纤的竖直高度
setnamed("core","radius",core_radius);
setnamed("core","x",0.0);
setnamed("core","y",0.0);
setnamed("core","z",0.0);
setnamed("core","z span",L);
setnamed("core","second axis","z");# 选择旋转轴为z轴（在这之间已设置绕x轴旋转了90度）
setnamed("core","rotation 2",-theta);# 旋转对应角度

# update cladding dimensions
setnamed("cladding","radius",cladding_radius);
setnamed("cladding","x",0.0);
setnamed("cladding","y",0.0);
setnamed("cladding","z",0.0);
setnamed("cladding","z span",L);
setnamed("cladding","second axis","z");
setnamed("cladding","rotation 2",-theta);

这里将core和cladding材料优先级设置为4和5.

仿真区域设置：

Ports分别位于光栅结构上方和光栅结构左侧。

port1：

这里的设置很奇怪，前文最开始说 这是一个 TE 绝缘体上硅 (SOI) 耦合器，但这里用的却是TM模式
TE 绝缘体上硅 (SOI) 耦合器

这里的index应该是模式的有效折射率

官网上的解释：

但是，结果跟通过以下步骤得到的有效折射率不同：

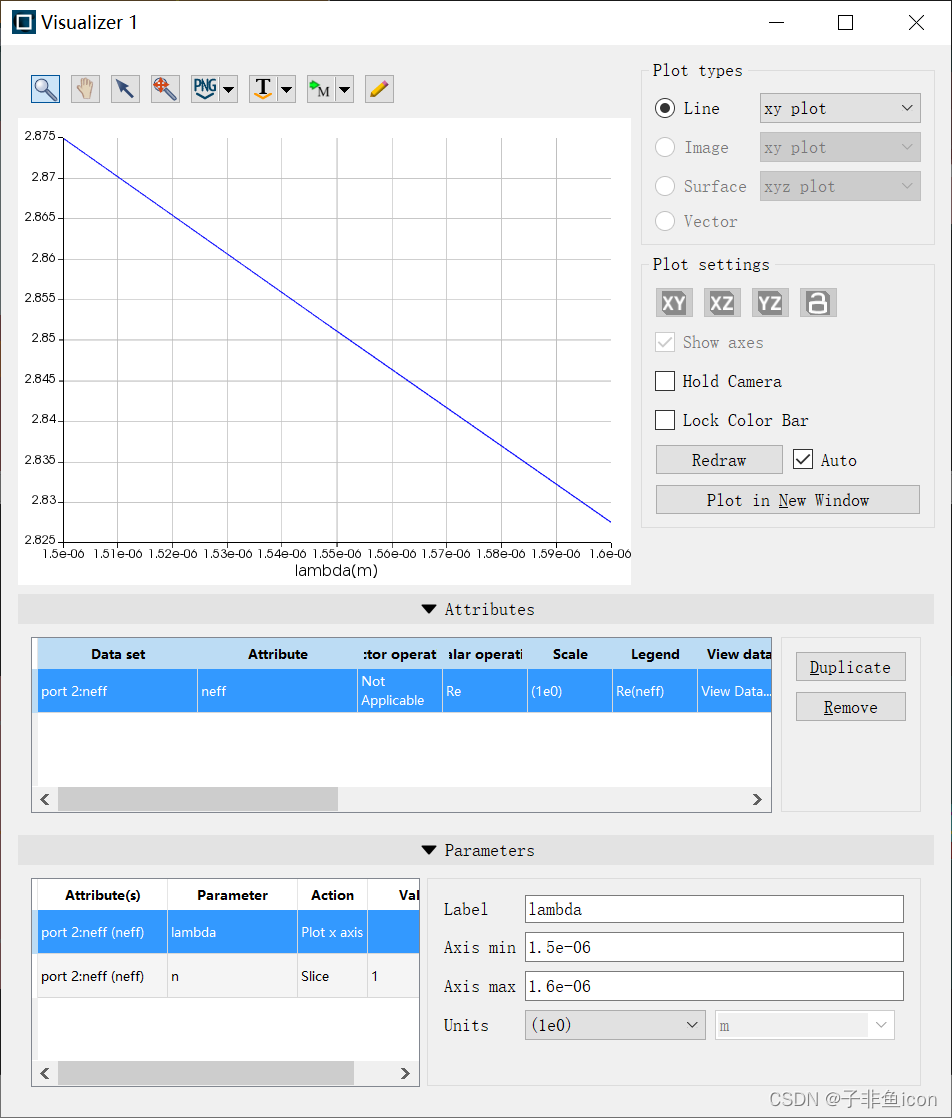
其实没太搞懂，他这里的index到底是个啥，会那么大，此处存疑。

2.1.2 优化和扫描

这个T结果，在model的分析组里

Setup的Variables

Setup的Script
（关于补偿这一点没太看懂tox offset和rotation offset各自的用处，可能要在论文中寻求答案了）

## This setup script keeps the port object on the fiber up to date with changes
## in the geometry of the fiber. It updates port 1 with the correct position, 
## injection angle and offset needed to excite selected port mode cleanly.

# 此设置脚本使光纤上的端口对象随着光纤几何形状的变化保持最新。
# 它使用正确的位置、注入角度和偏移来更新端口 1，以干净地激发选定的端口模式。

# fiber parameters
fiber_xpos = getnamed("fiber","x");#获得光纤的x位置
fiber_ypos = getnamed("fiber","y");
fiber_theta = getnamed("fiber","theta");
fiber_core_diameter = getnamed("fiber","core diameter");
fiber_yspan = getnamed("fiber","y span");

# top oxide parameters
tox_ypos = getnamed("SiO2 TOX","y");#包层的y位置

# port position
fiber_theta_rad = fiber_theta*(pi/180.0);
port_xpos = fiber_xpos + %tox offset% * sin(fiber_theta_rad);# 加上补偿
port_ypos = fiber_ypos + tox_ypos + %tox offset% * cos(fiber_theta_rad);
setnamed("FDTD::ports::port 1","x",port_xpos);# 仅设置端口1
setnamed("FDTD::ports::port 1","y",port_ypos);

# port angle
setnamed("FDTD::ports::port 1","theta",-fiber_theta);

# port offset
port_offset = 4*fiber_core_diameter*tan(fiber_theta_rad);
setnamed("FDTD::ports::port 1","rotation offset",port_offset);

getnamed

Analysis的Script

## Normalized power through port 2 at the target frequency.
# 目标频率下通过端口 2 的标准化功率。
## This result is needed  to optimize the coupling efficiency.
# 这个结果是优化耦合效率所需要的。

T_data = getresult("::model::FDTD::ports::port 2","T"); # 该数据既包含波长又包含透射率
T = abs(T_data.T);
lambda = T_data.lambda;
#lambda0 = (min(lambda)+max(lambda))/2.0;
ii = find(lambda,lambda0);
?T = T(ii); # 输出中心波长处的透射率

getresult

优化结果

2.2 第 2 步：3D 优化

1.打开 3D 模拟文件。
2.转到“对象树”（Objects Tree）窗口并选择光栅结构组（Objects Tree）。
3.左键单击选定的结构组，然后在上下文菜单中选择“编辑对象”（Edit object）以打开编辑窗口。在编辑窗口的“属性”（Properties）选项卡中，您应该会看到 2D 优化的最佳光栅周期和占空比。
4.单击“确定”关闭结构组编辑窗口。
5.现在，进入“优化和扫描”（Optimizations and Sweeps）窗口，选择名为位置优化（position optimization）的优化项。
6.运行选定的优化。这将需要几个小时，因为所有的模拟都是 3D 的。如果您不想等待，则直接进入 S 参数提取步骤。
7.优化完成后，可以检索最佳光纤位置和预测的耦合效率。左键单击位置优化项，选择“可视化”，然后选择“最佳参数”或“最佳形式”（“best parameters” or “best fom”.）。最佳参数结果包含最佳光纤位置 x，而最佳品质因数（figure of merit）结果包含目标波长处的耦合效率。

优化结束时的优化状态窗口也可以提供如下所示的相同信息：

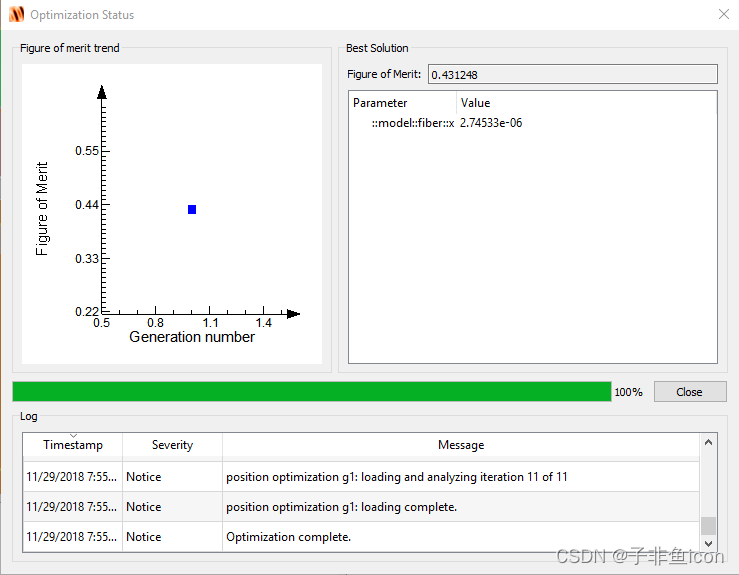
2.2.1 仿真结构

光栅结构，已是2D 优化的最佳光栅周期和占空比。

Script:

deleteall; # 删除当前组群范围内的所有实体对象

####################################################
# Grating coupler 3D
#
# Copyright Lumerical Solutions Inc
#####################################################

n_periods = ceil(%target length%/pitch);  # 光栅的周期数
fill_width = pitch*%duty cycle%;  # 未刻蚀的宽度
etch_width = pitch*(1-%duty cycle%);  # 刻蚀的宽度
L = n_periods*pitch + etch_width;  # 光栅部分的长度
theta = asin( 0.5*%y span%/radius ) * 180/pi; #计算扇形光栅结构的角度

# waveguide
addrect;
set("name","waveguide");
set("x min",-%waveguide length%); # 波导部分长度
set("x max",0);
set("y",0);
set("y span",%waveguide width%);# 波导部分的宽度
set("z min",0);
set("z max",%h total%);

# taper section 楔形部分
addcustom; # 添加自定义图形
set("x min",0);
set("x max",radius * cos(theta*pi/180));
set("z min",0);
set("z max",%h total%);
set("y span",%y span%); # y span为中间梯形部分y方向最大宽度
Ltaper = get("x span")*1e6; # 获得x span的数据，单位微米，中间部分的长度
w1 = %waveguide width%*1e6/2; # 中间梯形部分左边的竖边的一半
w2 = %y span%*1e6/2;# 中间梯形部分右边的竖边的一半
x0 = Ltaper/2; 
a = w2;
alpha = (w1-w2)/Ltaper^m;
format long;
equation = num2str(alpha)+"*("+num2str(x0)+"-x)^"+num2str(m)+"+"+num2str(a); # alpha*(x0-x)^m+a 参数m能让扇形斜边具有一定的弧度
set("equation 1",equation);# 将custom里的公式设置为如上所示
format short;

# input section 输入波导
addring;
set("name","input section");
set("inner radius",radius * cos(theta*pi/180));
set("outer radius",radius);
set("x",0);# 这里的x,y主要是指环的圆心，所以先都设置为0，再通过最后的move移动25
set("y",0);
set("z min",0);
set("z max",%h total%);
set("theta start",-theta);
set("theta stop",theta);


# lower layer below grating 光栅结构下的一层
if(%etch depth% < %h total%) {
  copy; # 拷贝所选择的实体对象，就是上一个环形，这样仅改变部分参数就可以，角度啥的可以不用再设置了
  set("name","lower layer");
  set("inner radius",radius);
  set("outer radius",radius+L);
  set("z min",0);
  set("z max",%h total%-%etch depth%);
}

# output section # 输出波导
copy;
set("name","output section");
set("inner radius",radius+L);
set("outer radius",radius+L+%L extra%);# L extra是输入波导的x上长度
set("z max",%h total%);

#add grating
for(i=1:n_periods){
  addring;
  set("x",0);
  set("y",0);
  set("z min",%h total%-%etch depth%);
  set("z max",%h total%);
  set("theta start",-theta);
  set("theta stop",theta);
  set("inner radius",radius + pitch*(i-1)+etch_width);
  set("outer radius",radius + pitch*i);

}

# set material and z span for all structures
selectall;
set("material",material); 
if(get("material")=="<Object defined dielectric>") 
  { set("index",index); } 
move(-radius,0,0); # 将整体的沿x移动-25的距离

addcustom

format

有关custom:

equation 1 用来定义x轴上部，y关于x的表达式。equation 2是定义下部分。


radius应该是除开光栅部分，前面一部分扇形的半径长度

copy

move

光纤部分：

优化部分：

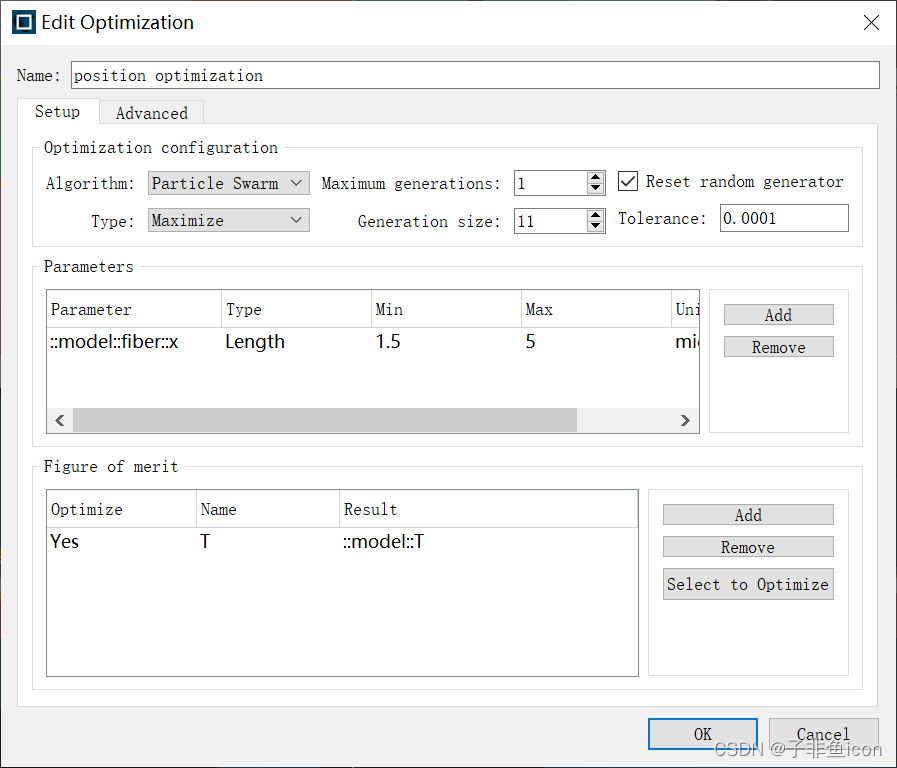
2.3 第 3 步：S 参数提取

1.再次转到“对象树”(Objects Tree)窗口并选择纤维结构组( fiber structure group)。
2.左键单击所选组，然后在上下文菜单中选择“编辑对象”(Edit object”)。
3.在编辑窗口的“属性”(Properties)选项卡中，应该存在最佳光纤位置 x。
4.再次，转到“优化和扫描”(Optimizations and Sweeps)窗口，选择名为 S-parameters 的扫描项并运行扫描。扫描将启动两个模拟，应该在大约半小时内完成。
5.扫描完成后，设备的散射参数变为可用。要查看它们，左键单击 S 参数扫描项并选择“可视化”(Visualize)，然后在上下文菜单中选择“S 参数”(S parameters)。选择标量运算“Abs^2”以查看幂 s 参数
6.要导出 S 参数结果，左键单击 S 参数扫描项，然后在上下文菜单中选择“导出到 INTERCONNECT”。在随后的“Export to INTERCONNECT”窗口中，输入数据文件的名称和位置，然后单击“Save”。

获得的 s 参数光谱表明在目标波长处的功率耦合效率约为 40%，如下图所示：

有关 s 参数提取的更多信息，请参阅此示例的附录部分。

2.3.1 优化设置

2.4 第 4 步：创建紧凑模型

1.在 INTERCONNECT 中打开 grating_coupler.icp 文件。
2.将步骤 3 中生成的 S 参数文件导入到 Optical N Port S -Parameter元件 (Grating_Coupler)。
3.运行仿真并可视化输入 1 模式 1 的传输结果。将标量操作切换到“Abs^2”以观察功率传输

在 INTERCONNECT 中测量的功率传输与步骤 3 中获得的 s 参数功率传输相同。

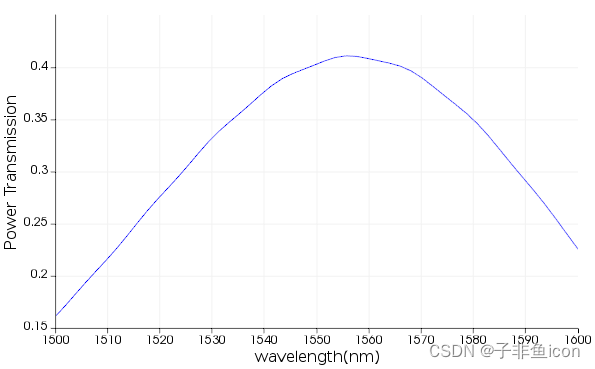
三、重要的模型设置

此模型中使用的重要对象和设置的描述

极化（Polarization）

选择的折射率值代表 SOI 芯片制造工艺。由于硅和氧化硅之间的高折射率对比，集成波导的两种基本模式（TE 和 TM）的有效折射率之间存在很大差异。因此，SOI 光栅耦合器具有很强的偏振选择性。所呈现的设计激发了 TE 模式，因为这是最常见的选择，但是，也可以针对 TM 模式设置优化。

倾斜角度（Tilting angle）

耦合效率在很大程度上取决于光纤如何与顶部氧化硅包层相遇。在本例中，假设光纤末端以小角度抛光，这样光纤在安装到顶部包层时会倾斜。这种倾斜防止反射进入光纤。为简单起见，此处采用了固定的倾斜角度，但是，可以通过允许其变化来改进设计。

蚀刻深度（Etch depth）

耦合效率对光栅的周期、占空比和蚀刻深度高度敏感。为简单起见，此处采用固定的蚀刻深度，但是，如果可用的制造工艺提供该自由度，它也可以改变。

衬底（Substrate）

如果制造的器件中存在硅衬底，则应将其包括在模拟中。基板将对光的耦合方式产生显着影响，并且不能像其他设备设计中经常做的那样被忽略。

周期（Pitch）

在最初的二维优化步骤中，如何选择光栅周期的优化范围并不明显。 假设固定的蚀刻深度 $h_e$ 和 [0,1] 范围内的占空比 $d$，什么是合适的周期范围？ 这里使用的范围值来自最低阶布拉格条件，它将光栅的周期$p$与光栅的有效折射率 $n_{eff}$相关联：

$p=\frac{{\lambda }_0}{n_{eff}-n_{Si{O}_2}sin(\theta )}$

其中 ${\lambda }_0$ 是中心波长，$n_{Si{O}_2}$ 是氧化硅顶部包层的折射率，θ 是与之前一样的源角。 请注意，此关系假定顶部包层和纤芯之间的折射率对比是最小的，并且对于高折射率对比系统无效。 在优化过程中为周期选择的范围可以通过考虑$n_{eff}$的两个极值来获得，$n_{eff}$ 是光栅的未蚀刻和部分蚀刻区域的平板模式的有效折射率。 这些折射率可以通过本征模式求解器（例如 FDE）获得。 最佳 $p$值通常略大于布拉格条件预测的值。 由于波导上的端口包含平板模式的有效折射率作为其结果之一，因此该初始猜测很容易计算。

结构组（Structure groups）

这里使用结构组来更新光栅和光纤的几何图元。 必须使用结构组的界面应用对光栅和光纤参数的任何更改。 使用结构组的优点是它们可以将单个参数更改应用于多个图元，但是，它们也可以覆盖单个几何图形的手动更改。 设置光纤结构组以模拟以一定角度抛光的光纤。 这是通过对组中的对象应用轻微旋转并为对象使用“网格顺序”（mesh order）设置来完成的，这样光纤只向下延伸到光栅耦合器上方的某个点，而不是像可能的那样一直穿过光纤 从布局视图描绘。 这可以通过可视化结构的折射率分布来验证，如下所示：

优化品质因数 (Optimization figure of merit，FOM)

由于设计的目的是在所需波长处获得最佳可能耦合，因此优化品质因数被选择为在目标波长处通过耦合器的传输，并且优化算法将尝试最大化该值。 该品质因数由“模型”（model）对象中的分析脚本（analysis script）计算得出。

四、使用您的参数更新模型

根据您的设备参数更新模型的说明

1.在全局端口设置中输入所需的源波长和目标带宽。
2.从模型对象的分析选项卡中选择用于耦合效率优化的目标波长。
3.根据您的测量设备更新光纤尺寸和折射率值。
4.根据您的制造工艺和目标设计偏振修改折射率值和层厚度（见下一节）。
5.验证两个端口的选定模式是否具有所需的极化； 必要时调整端口大小。
6.使用您选择优化的参数更新优化对象； 选择合适的参数范围（见下一节）。

五、CML 编译器的参数提取

用于 CML 编译器的参数提取说明以生成紧凑模型

本节介绍如何使用脚本文件自动提取和保存光栅耦合器的 S 参数。 我们假设光栅耦合器已经优化，因此只需要概述部分中原始工作流程的第 3 步（Step 3)。 此步骤生成的 S 参数文件可以直接在 CML Compiler 中使用，以创建光栅耦合器的紧凑模型。 请注意，CML 编译器的运行超出了本示例的范围。 有关更多信息，请参阅 CML 编译器概述。

1.打开仿真文件 grating_coupler_3D.fsp 和脚本文件 2.grating_coupler_dataCMLCompiler.lsf。
运行脚本文件。

grating_coupler_dataCMLCompiler.lsf

###########################################################
# Script file: grating_coupler_dataCMLCompiler.lsf
#
# Description: This file can be used to extract the S-parameters
#	required by the CML Compiler to build a grating coupler
#	element
# 说明：此文件可用于提取 CML 编译器构建光栅耦合器元件所需的 S 参数
# Copyright 2019, Lumerical Solutions, Inc.
###########################################################

###########################################################

# run S-parameter sweep
runsweep("S-parameters");  # 运行参数扫描

# export S-parameter data for CML Compiler
exportsweep("S-parameters","grating_coupler.dat");#官网都没找到这个函数

六、让模型更进一步

为想要进一步定制模型的用户提供的信息和提示

S 参数：S 参数提取步骤仅生成 TE 偏振的散射参数结果。要添加 TM 偏振，只需在集成波导端口上同时选择 TE 和 TM 模式，然后重新运行 S 参数扫描。此更改将为 S 参数扫描添加一个额外的模拟和一个额外的结果。

2D 优化：可以通过将光栅的蚀刻深度和光纤的倾斜角添加到优化参数列表中来改进初始的 2-D 优化步骤。改变蚀刻深度可以提高初始耦合效率，而改变倾斜角可以使峰值效率正好落在中心波长处。根据设计目标，其他品质因数（例如整个频谱上的平均传输）也可用于优化。

3D 优化：可以通过包含多个优化参数来改进最终的 3-D 优化步骤。也可以完全绕过 2-D 优化步骤并使用 3-D 模型来优化所有五个参数。增加更多的优化参数将大大增加完成优化阶段所需的时间，但是，它可以提高最终设计的耦合效率。

锥度优化：3-D 耦合器模型使用绝热锥度部分将集成波导连接到光栅的起点。通过优化锥形形状也可以提高耦合效率（参见 SOI 锥形设计）。

并行化：如果您可以访问一组机器，优化工具可以使用作业管理器来并行化所有需要的模拟。并行化可以大大减少优化时间，因为给定优化生成的所有模拟都可以在不同的机器上独立运行。

MATLAB 和 Python：为了支持不同的优化算法，Matlab 和 Python API 可用于连接其他工具，例如 Matlab 优化工具箱或 SciPy 的优化包。

高效光栅耦合器：在大带宽上效率高于 90% 的耦合器采用 FDTD 设计，采用更复杂的光栅和混合 2-/3-D 优化策略（参见参考资料）。

七、其他资源

其他文档、示例和培训材料

相关出版物

1.Basic grating coupler design : D. Taillaert, F. Van Laere, M. Ayre, W. Bogaerts, D. Van Thourhout, P. Bienstman and R. Baets, “Grating Couplers for Coupling between Optical Fibers and Nanophotonic Waveguides,” Japanese Journal of Applied Physics, vol. 45, no. 8a, pp. 6071-6077, 2006.
2.Advanced optimization : R. Marchetti, C. Lacava, A. Khokhar, X. Chen, I. Cristiani, D. J. Richardson, G. T. Reed, P. Petropoulos and P. Minzioni, “High-efficiency grating-couplers: demonstration of a new design strategy,” Scientific Reports, Article number: 16670, 2017. ; T. Watanabe, M. Ayata, U. Koch, Y. Fedoryshyn and J. Leuthold, “Perpendicular Grating Coupler Based on a Blazed Antiback-Reflection Structure,” Journal of Lightwave Technology, vol. 35, no. 21, pp. 4663- 4669, 2017.

八、附录

其他背景信息和理论

从无源光子器件的组件级仿真中提取 S 参数

S 参数矩阵形式是构建用于电路级仿真的光子器件紧凑模型的常用方法。假设设备对光信号的响应是线性的，则可以通过具有多个网络端口的网络（黑盒）对其进行建模，其中每个网络端口接收输入信号并散射或反射输出信号。

我们假设该设备有 N 个物理端口（通常是输入/输出波导通道），并且每个端口都支持一定数量的感兴趣的模式。 S 参数矩阵的每个元素是两个物理端口中光学模式的复包络之间的比率。例如，为了模拟 1x2 MMI 的输入/输出波导通道中基本 TE 和 TM 模式的行为，我们需要一个 6x6 S 参数矩阵，因为三个物理端口中的每一个都有两个模式。 S 参数矩阵的每一列对应一个固定的输入物理端口和模式，每一行对应一个固定的输出物理端口和模式。

提取光子器件 S 参数矩阵的方法取决于所使用的求解器。在 FDTD 和 EME 求解器中，可以在每个物理端口上设置端口对象。用于 S 参数提取的求解器之间的主要区别是：

$\cdot$FDTD 每次模拟在一个输入端口对象中注入一种模式，而 EME 可以在一次模拟中求解 S 矩阵的所有元素；
$\cdot$FDTD 是宽带的，因此可以在一次模拟中计算出许多频率点，而 EME 的结果是每次模拟的单个频率。

因此，在这两种求解器中，都需要运行扫描以获得多个频率值的完整 S 参数矩阵，方法是扫描输入物理端口和模式或频率点。

使用“案例库”( Application Gallery)中的示例为您的组件确定合适的求解器。一旦您确定了合适的求解器，本节将介绍 S 参数提取和导出到 INTERCONNECT 的推荐方法。

在本节中，我们将描述如何：

对于 FDTD，计算 S 参数矩阵并将其保存到具有适当格式的文件中，以便在 INTERCONNECT 中的光学 N 端口 S 参数基元元素中导入。
对于 EME，计算 S 参数矩阵并将其保存到具有适当格式的文件中，以便在 INTERCONNECT 中的光学 N 端口 S 参数基元元素中导入。
可选地，更准确地考虑设备的群延迟。 这对于将成为相敏电路一部分的元件（例如，腔体、谐振结构和干涉装置）很重要。 我们将使用 S 参数文件中的群延迟规范，这是 INTERCONNECT 中光学 N 端口 S 参数元件的数字滤波器中的群延迟选项所必需的。

其他附录见网页