算法设计大赛T15 - T16

T15 有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。

思路：
图论中的问题，思路大致为将所有与第i个省份连接的其他省份都存储在列表province[i]中（类似于邻接矩阵的每一行），全部储存完毕后再遍历province，合并每个与privince[i]有交集的其他省份，并将其他省份置空。这样，我们便可以得到一存储相连省份与空列表的province，求得其中非空列表的个数即为所求解，代码如下：

class Solution:
    def findCircleNum(self, isConnected: List[List[int]]) -> int:
        province = [[] for i in range(len(isConnected))]
        for i in range(len(isConnected)):
            for j in range(len(isConnected[0])):
                if isConnected[i][j] == 1:
                    province[i].append(j)
        for i in range(len(province)):
            f = 1
            while f == 1:
                f = 0
                for j in province[i]:
                    if province[j] != [] and i!=j:
                        province[i] += province[j]
                        province[j] = []
                        f = 1
        res = 0
        for i in province:
            if i!=[]:
                res += 1
        return res

运行结果：

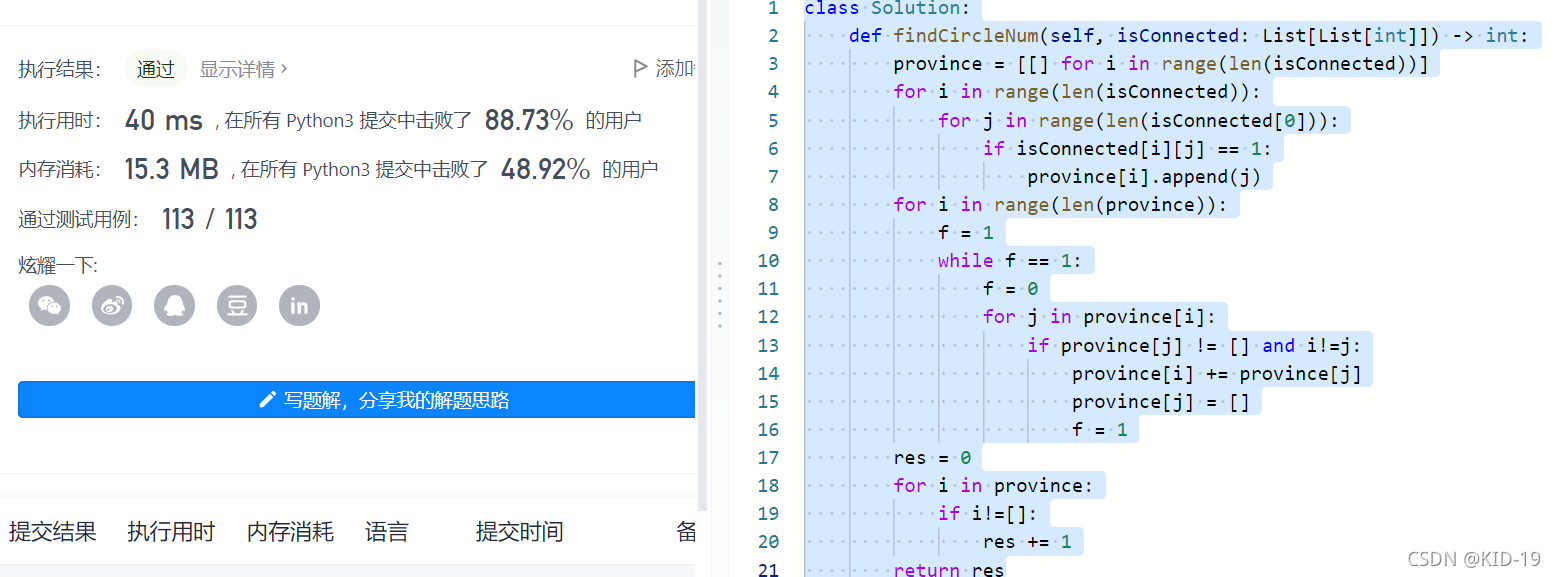
T16 有 n 个网络节点，标记为 1 到 n。
给你一个列表 times，表示信号经过 有向 边的传递时间。 times[i] = (ui, vi, wi)，其中 ui 是源节点，vi 是目标节点， wi 是一个信号从源节点传递到目标节点的时间。
现在，从某个节点 K 发出一个信号。需要多久才能使所有节点都收到信号？如果不能使所有节点收到信号，返回 -1

思路：
求所需最大时间，则为求从起点到最“远”端所需的最大距离（时间）。
从起点k出发，将所有节点分为两类，一类为可以与起点直接确定距离的节点，另一类则为暂时不能直接与起点确定距离的节点，使用dist储存起点与所有节点的距离（未确定则用inf代替）。
建立邻接矩阵graph储存图，使用used记录节点是否已被连接；循环n次，每次连接起点与可确定节点中距离最小的节点，之后更新dist，若i点相对于起点和正在循环的节点x仍无法确定距离，则dist[i]仍未inf，若可以确定距离，dist[i]更新为min(dist[i],dist[x]+graph[x][i])。
循环结束后，若dist中仍存在inf则说明存在无法确定距离的节点（叶子节点），返回-1；否则，返回max(dist)作为最终结果

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        graph = [[float('inf') for _ in range(n)] for _ in range(n)]
        for i,j,p in times:
            graph[i-1][j-1] = p
        dist = [float('inf')] * n
        dist[k-1] = 0
        used = [False] * n
        for _ in range(n):
            x = -1
            for i in range(n):
                if used[i]==False and (x==-1 or dist[x]>dist[i]):
                    x = i
            used[x] = True
            for i in range(n):
                dist[i] = min(dist[i],dist[x]+graph[x][i])
            res = max(dist)
        if res == float('inf'):
            return -1
        return res

运行结果: