功率分析仪FFT与窗函数

任何波形都可以由多个正弦波叠加而产生，时域波形无法观察到其中包含的幅值较小的其他信号成分；频域图，可以明显分辨出其中的小信号成分。
DFT傅里叶变换分析基本思想就是任意函数可以分解为无穷多个不同频率正弦信号的和。DFT直接计算包含大量重复的cos、sin计算，FFT的作用就是用技巧减少cos、sin项目的重复计算。

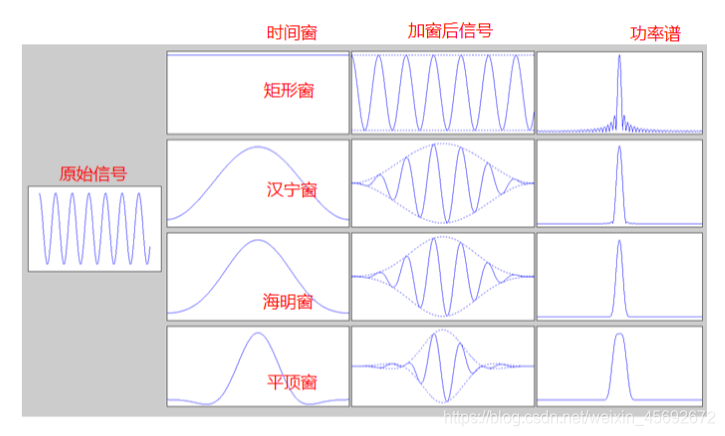
1.FFT为什么要加窗函数？
因FFT是对有限波形数据进行计算，与原始的连续信号的分析结果之间会存在误差，使用窗函数可以减少对波形的截断产生的泄露问题。

2.FFT几种典型窗函数特点及应用：
1）矩形窗：适用于瞬态信号的分析。
例如，脉冲信号，其幅值在时间窗内已全部衰减。通常，矩形窗，对连续信号不合适。其功率谱旁瓣较多，泄露较大。
2）汉宁窗：适用于连续信号的分析。
作用：使信号在窗函数的起点和终点逐步衰减到零。
特点：频率分析准确度较高，幅值准确度较低；对于连续信号的分析，功率谱主瓣较窄，即分析频率很强。
3）海明窗：改进的汉宁窗，第一旁瓣衰减比汉宁窗大，适合应用于区分主瓣、第一旁瓣幅值。
4）平顶窗：适用于连续信号的分析。
作用：使信号在窗函数的起点和终点逐步衰减到零。
特点：频率分析准确度较低，幅值准确度较高；对于连续信号的分析，功率谱主瓣较宽，即分析幅值很强。