YOU ONLY SEARCH ONCE: SINGLE SHOT NEURAL ARCHITECTURE SEARCH VIA DIRECT SPARSE OPTIMIZATION

研究的问题

问题：在巨大的搜索空间，如何有效的搜索的网络结构。
方法：从剪枝的角度出发，对结构系数使用稀疏正则化（$L_1$范数），获得一个高效的网络架构。

预备知识

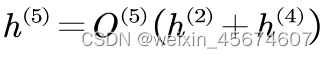
这里以五号节点为例，$h^{(}5)$表示五号结点的输出；$O^{(5)}$表示结点内部的操作；$h^{(2)},h^{(4)}$表示五号结点对应的输入。

以中间结点$i$为例，则其搜索结构的输出表达式：

其中，N表示候选操作的个数,${\alpha }_{(i,j,k)}$ 表示结点i和结点j选择操作k的概率,$o_{(i,j,k)}$表示结点i和结点j的第k个候选操作相关参数；${\alpha }_i$表示结点i的结构系数矩阵；$w_i$表示结点i的参数矩阵。

以中间结点$i$与其他节点的第 $j$个操作为例。则其搜索结构的输出表达式：

搜索空间

如上图所示，这里对于当前的cell单元来说，首先是在DAG（有向无环图）中进行搜索；然后对冗余的结构进行剪枝，获得网络的结构；最后利用残差连接将cell单元的输出连接起来作为下一个cell单元的输入。整个DNN网络都是在相似的cell单元堆叠而成。那么针对该基本单元的第b块第i层的第J次操作的输出可以这样表示：

其中$O_{(b,i,j)}$表示对应位置操作，也可以理解为参与运算的权重参数；${\lambda }_{(b,m,n)}^{(i,j)}{h}_{(b,m,n)}$表示作为当前操作的输入，具体来说包括前$i-1$个层的$N$个操作对应的输出;${\lambda }_{(b,0,0)}^{i,j}{O}_{(b-1)}$表示整个cell单元的输入。

整个基本结构单元的表达式

优化和训练

目标函数

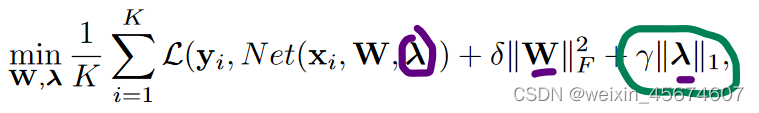
其中$w$表示具体操作结构的权重参数，$\lambda$表示结构系数，也就是我们需要稀疏化的对象，$x_i$表示训练数据；$y_i$表示训练数据的目标标签；$\delta$和$\gamma$表示对权重和结构系数的惩罚权重。

针对$\lambda$的稀疏优化

作者这里采用APG-NAG优化器去优化结构系数，其核心公式如下：

其中，$t$表示迭代的次数；$\eta (t)$表示梯度更新的步长；$\mu (t-1)$表示动量；$S_{\eta (t)\gamma }$表示软阈值算子,$S_{\alpha }=sign(z_i)(|z_i|-\alpha )$。

存在问题

由于存在过拟合的风险，使得该优化器不适用；

解决方案

将数据分为两部分，在训练权重$w$和结构稀疏$\lambda$的时候，两者分开训练。

纳入不同的预算

原因：由于硬件条件的限制，在搜索过程中，会导致内存不够。故在对结构系数$\lambda$的惩罚权重进行改进；
观察：在所有$\gamma$都固定的情况下，每个reduction cell块的复杂度远高于其他块。
具体公式如下：

其中,分子表示第$t$次迭代，$\lambda$确定结构的FLOP，分母表示整个单元的FLOP。

实验结果

cifar

ILSVRC 2012

###消融实验

“Search space”指的是是否共享结构系数矩阵；"Pre-train"是指我们是否在搜索中进行步骤一。而"Split training"是指是否将整个训练集拆分为两组分别进行权重和结构学习。W & S的比值表示用于权重学习和结构学习的训练样本的比值。对于x：y的比例，我们对每一次x + y迭代更新x次权重，更新y次λ。注意，我们只在权重学习集上预训练模型。

值得注意的是，使用单独的集合进行结构学习对防止训练数据过拟合起到了重要作用，性能提高了0.2 %。这两个集合的比例影响较小。此外，一个好的权重初始化也是至关重要的，因为在相同的参数预算下，随机初始化权重可能导致另外0.2 %的精度下降。