牛客练习赛81 D - 小Q与树 (点分治)

最新推荐文章于 2024-02-18 21:42:40 发布

tzteyang

最新推荐文章于 2024-02-18 21:42:40 发布

阅读量238

点赞数 1

分类专栏：数据结构 # 点分治图论

本文链接：https://blog.youkuaiyun.com/weixin_45672411/article/details/116271867

版权

数据结构同时被 3 个专栏收录

31 篇文章

订阅专栏

图论

5 篇文章

订阅专栏

点分治

2 篇文章

订阅专栏

本文介绍了一种使用点分治算法解决树上路径统计问题的方法，通过排序节点权重并计算子树贡献，实现了O(nlogn)的时间复杂度。文章详细讲解了算法思路，包括如何统计路径上的最小值乘积，并给出了C++实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

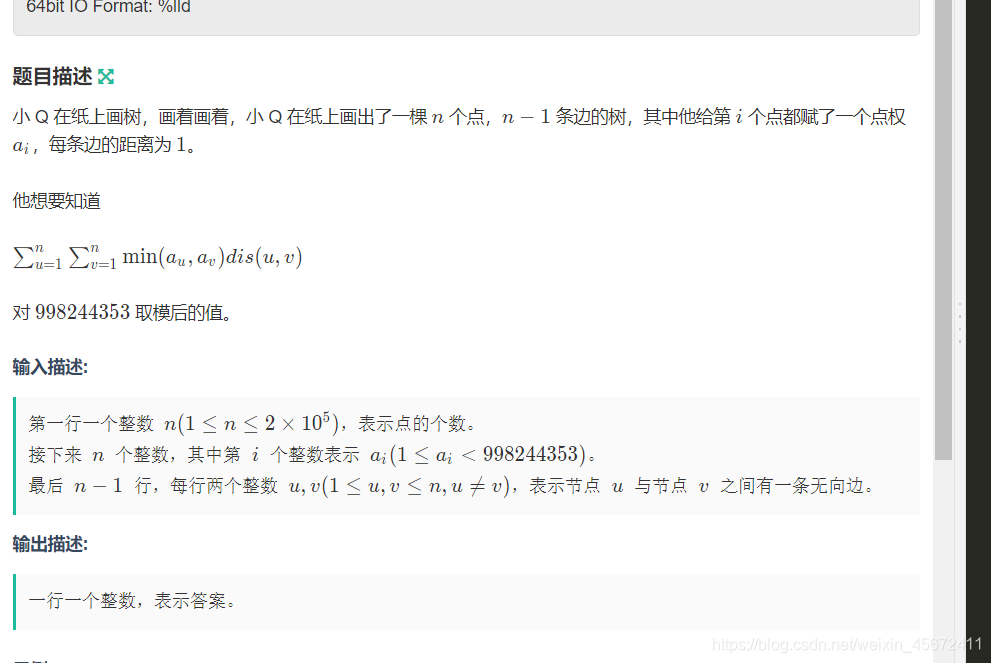
在这里插入图片描述
思路：
一看到树上的路径统计问题而且还可以接受 $O (n l o g n)$ 的复杂度，就可以往点分治的方向考虑一下。
这道题的关键就是怎么 $O (n)$ 的统计一下当前一棵树内的 $\sum_{u=1}^{n}\sum_{v=1}^{n}min(a_u,a_v)dis(u,v)$ ，我们可以从这个 $m i n$ 下手去考虑每个点权值 $a_i$ 会对答案产生的贡献。
点分治考虑经过当前树的根节点的路径， $d i s (u, v)$ 就拆成了 $d i s (u, r o o t) + d i s (r o o t, v)$ ，再用容斥原理去除不经过根节点的路径就可以得到答案了。

我们把 $a$ 数组从小到大排个序之后，当前位置的 $a_i$ 在和后面的点组合时都会产生的 $a_i$ 的贡献，我们用 $p a i r$ 存一下点权值和相应的距离，维护一个前缀和数组就算区间内的距离和，就可以 $O (n)$ 的算答案了。

复习一下淀粉质

#include <bits/stdc++.h>

using namespace std;

#define pb push_back
#define eb emplace_back
#define MP make_pair
#define pii pair<int,int>
#define pll pair<ll,ll>
#define lson rt<<1
#define rson rt<<1|1
#define CLOSE std::ios::sync_with_stdio(false)
#define sz(x) (int)(x).size()
typedef long long ll;
typedef double db;
const int INF = 0x3f3f3f3f;
const db eps = 1e-6;
const ll MOD = 998244353;
const int N = 2e5 + 10;
int n,head[N],tot;
bool vis[N];
ll a[N];
struct node {
	int next,to;
}edge[N<<1];
void addedge(int u,int v) {
	edge[++tot].to = v,edge[tot].next = head[u],head[u] = tot;
	edge[++tot].to = u,edge[tot].next = head[v],head[v] = tot;
}
int root,max_son[N],siz[N],maxx,SIZE;
void GetRoot(int u,int fa) {//找重心
	siz[u] = 1; max_son[u] = 0;
	for(int i = head[u];i;i = edge[i].next) {
		int v = edge[i].to;
		if(vis[v] || fa == v) continue;
		GetRoot(v,u);
		siz[u] += siz[v];
		max_son[u] = max(max_son[u],siz[v]);
	}
	max_son[u] = max(max_son[u],SIZE-max_son[u]);
	if(maxx > max_son[u]) maxx = max_son[u],root = u;
}

std::vector<pll>tmp;
void dfs(int u,int fa,int d) {
	// dis[u] = d;
	tmp.pb(MP(a[u],1ll*d));
	for(int i = head[u];i;i = edge[i].next) {
		int v = edge[i].to;
		if(vis[v] || v == fa) continue;
		dfs(v,u,d+1);
	}
}
bool cmp(pll a,pll b) {
	return a.first < b.first;
}

// ll sum[N],ans;
ll ans;
ll sum[N];
ll cal(int u,int len) {
	tmp.clear();
	dfs(u,0,len);//以u为根 重新统计一遍子树答案
	sort(tmp.begin(),tmp.end(),cmp);
	for(int i = 1;i <= sz(tmp);i ++) sum[i] = (sum[i-1] + tmp[i-1].second) % MOD;
	ll num = sz(tmp) - 1,res = 0;
	for(int i = 0;i < sz(tmp);i ++) {
		int r = sz(tmp),l = i + 2;
		res = (res + tmp[i].second * tmp[i].first % MOD * num % MOD) % MOD;
		res = (res + tmp[i].first * (sum[r] - sum[l-1]) % MOD) % MOD;
		num--;
	}
	return res * 2 % MOD;
}
void divide(int u) {
	ans = (ans + cal(u,0)) % MOD;
	vis[u] = 1;
	for(int i = head[u];i;i = edge[i].next) {
		int v = edge[i].to;
		if(vis[v]) continue;
		ans = (ans - cal(v,1) + MOD) % MOD;
		SIZE = siz[v];
		maxx = INF;
		root = 0;
		GetRoot(v,u);
		divide(root);
	}
}
//看到 树上路径 很自然得去想点分治了
int main() {	
	scanf("%d",&n);
	for(int i = 1;i <= n;i ++) {
		scanf("%lld",&a[i]);
	}
	int a,b;
	for(int _ = 1;_  < n; _ ++) {
		scanf("%d%d",&a,&b);
		addedge(a,b);
	}
	maxx = INF;
	SIZE = n;
	GetRoot(1,0);
	// cout << root << '\n';
	divide(root);
	printf("%lld\n",ans);
	return 0;
}