递归与分治策略

递归算法

程序直接或间接调用自身的编程技巧
一个过程或函数在其定义或说明中又直接或间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解，递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量。
递归需要有边界条件、递归前进段和递归返回段。

• 当边界条件不满足是，递归前进；
• 当边界条件满足时，递归返回。
• 注意：在使用递增归策略时，必须有一个明确的递归结束条件，称为递归出口，否则将无限进行下去（死锁）。
  递归的缺点：
  解题的运行效率较低。
  在递归调用过程中，系统为每一层的返回点、局部变量等开辟了堆栈来存储。递归次数过多容易造成堆栈溢出等。

Fibonacci数列：
当n=0，1时，F(n) = 1;
当n>1时，F(n) = F(n-1) + F(n-2);

Fibonacci数列的递归算法
int fib(int n)
{
	if (n<=1) return 1;
	return fib(n-1)+fib(n-2);
}

Fibonacci数列的递推算法
int  fib[50];			//采用数组保存中间结果
void fibonacci(int n)
{
	fib[0] = 1;	
	fib[1] = 1;
	for (int i=2; i<=n; i++)
		fib[i] = fib[i-1]+fib[i-2];
}

整数划分问题
整数划分问题是算法中的一个经典命题之一。把一个正整数n表示成一系列正整数之和：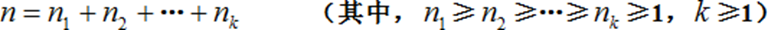
正整数n的这种表示称为正整数n的划分。正整数n的不同划分个数称为正整数n的划分数，记作 P(n) 。

分析：

1. 当n=1时，无论m为什么值，只有一种划分。F(1,m) = 1, m>=1.
2. 当m=1时，无论n的值为什么，只有一种划分。F(n,1) = 1, n>=1。
3. 当m>=n时，最大加数实际上不能超过n。F(n,m)=F(n,n)。
4. 当n=m时，F(n,n) = 1 + F(n,n-1)。
5. 当n>m时，F(n,m) = F(n,m-1) + F(n-m,m)。

#include <iostream>

using namespace std;

int fen(int n,int k)
{
    if(n==1||k==1)
        return 1;
    if(n<=k)
        return fen(n,n-1)+1;
    if(n>k)
        return fen(n,k-1)+fen(n-k,k);
    return 0;
}
int main()
{
    int n;
    cin>>n;
    cout<<fen(n,n)<<endl;
    return 0;
}

分治策略

分治策略是对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同。
递归地解这些子问题，然后将各子问题的解合并得到原问题的解。
分治法的基本步骤：

1. 分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；
2. 解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题；
3. 合并：将各个子问题的解合并为原问题的解。

分治法的适用条件：

1. 该问题的规模缩小到一定的程度就可以容易地解决；
2. 该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质；
3. 利用该问题分解出的子问题的解可以合并为该问题的解；
4. 该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

输油管道问题
某石油公司计划建造一条由东向西的主输油管道。该管道要穿过一个有n口油井的油田。从每口油井都要有一条输油管道沿最短路经（或南或北）与主管道相连。
如果给定n口油井的位置，即它们的x坐标（东西向）和y坐标（南北向），应如何确定主管道的最优位置，即使各油井到主管道之间的输油管道长度总和最小的位置？
给定n口油井的位置，编程计算各油井到主管道之间的输油管道最小长度总和。
输入：
第1行是一个整数n，表示油井的数量（1≤n≤10 000）。
接下来n行是油井的位置，每行两个整数x和y（﹣10 000≤x，y≤10 000）。
输出：
各油井到主管道之间的输油管道最小长度总和。

#include <bits/stdc++.h>
using namespace std;
int main()
{
	int n;				
	int x;					
	int a[1000];	
	cin>>n;
	for (int i=0; i<n; i++)
		cin>>x>>a[i];
	int y = select(0, n-1, n/2);
	int min=0;
	for(int i=0;i<n;i++)
		min += (int)fabs(a[i]-y);
	cout<<min<<endl;
}